当前位置:网站首页>[noi simulation] juice tree (tree DP)
[noi simulation] juice tree (tree DP)
2022-07-05 08:27:00 【DD(XYX)】
Topic
The original title is :「 Cattle guest 31454H」Permutation on Tree


Answer key
We take apart the absolute value symbols
∑ i = 1 n − 1 ∣ P i + 1 − P i ∣ = ∑ i = 1 n − 1 ( P i + 1 − P i ) [ P i + 1 > P i ] + ( P i − P i + 1 ) [ P i + 1 < P i ] \sum_{i=1}^{n-1}|P_{i+1}-P_i|=\sum_{i=1}^{n-1}(P_{i+1}-P_i)[P_{i+1}>P_i]+(P_{i}-P_{i+1})[P_{i+1}<P_i] i=1∑n−1∣Pi+1−Pi∣=i=1∑n−1(Pi+1−Pi)[Pi+1>Pi]+(Pi−Pi+1)[Pi+1<Pi]
Then for each number x x x, Calculate its coefficient as 1 The number and coefficient of schemes are -1 Number of alternatives .
Take the coefficient as 1 For example .
The original number of global schemes is through a simple DP( d p [ x ] = ( s i z [ x ] − 1 ) ! ∏ x → y d p [ y ] s i z [ y ] ! dp[x]=(siz[x]-1)!\prod_{x\rightarrow y}\frac{dp[y]}{siz[y]!} dp[x]=(siz[x]−1)!∏x→ysiz[y]!dp[y]) Calculated , We should give special consideration to x x x , Just cut the whole arrangement into two halves , On the tree, it shows as cutting x x x The subtree of ( Calculate the number of internal schemes of the subtree separately ), Then select some of the remaining trees and put them in the arrangement x x x Behind . meanwhile , We have to give x x x Find a partner Find a neighbor to match . So the design state :
- d p 0 [ i ] [ j ] dp0[i][j] dp0[i][j] : Just consider i i i Inside the subtree of , Let go of j j j A to x x x Behind , Not given x x x Number of paired schemes .
- d p 1 [ i ] [ j ] dp1[i][j] dp1[i][j] : Just consider i i i Inside the subtree of , Let go of j j j A to x x x Behind , The subtree has been given x x x Number of paired schemes .
When we merge two subtrees A , B A,B A,B when ,
d p 0 ′ [ r o o t ] [ j + k ] ← d p 0 [ A ] [ j ] ⋅ d p 0 [ B ] [ k ] ⋅ ( s i z [ A ] + s i z [ B ] s i z [ A ] ) ⋅ ( i + k i ) d p 1 ′ [ r o o t ] [ j + k ] ← d p 0 [ A ] [ j ] ⋅ d p 1 [ B ] [ k ] ⋅ ( s i z [ A ] + s i z [ B ] − 1 s i z [ B ] − 1 ) ⋅ ( i + k i ) ← d p 1 [ A ] [ j ] ⋅ d p 0 [ B ] [ k ] ⋅ ( s i z [ A ] + s i z [ B ] − 1 s i z [ A ] − 1 ) ⋅ ( i + k i ) dp0'[root][j+k]\leftarrow dp0[A][j]\cdot dp0[B][k]\cdot {siz[A]+siz[B]\choose siz[A]}\cdot {i+k\choose i}\\ dp1'[root][j+k]\leftarrow dp0[A][j]\cdot dp1[B][k]\cdot {siz[A]+siz[B]-1\choose siz[B]-1}\cdot {i+k\choose i}\\ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ \,\leftarrow dp1[A][j]\cdot dp0[B][k]\cdot {siz[A]+siz[B]-1\choose siz[A]-1}\cdot {i+k\choose i} dp0′[root][j+k]←dp0[A][j]⋅dp0[B][k]⋅(siz[A]siz[A]+siz[B])⋅(ii+k)dp1′[root][j+k]←dp0[A][j]⋅dp1[B][k]⋅(siz[B]−1siz[A]+siz[B]−1)⋅(ii+k) ←dp1[A][j]⋅dp0[B][k]⋅(siz[A]−1siz[A]+siz[B]−1)⋅(ii+k)
then , if i i i No x x x The ancestors of the , There can be
d p 0 [ i ] [ s i z [ i ] ] ← d p 0 [ i ] [ 0 ] dp0[i][siz[i]]\leftarrow dp0[i][0] dp0[i][siz[i]]←dp0[i][0]
if i i i Than x x x Small ( And x x x The coefficient of pairing is 1), Yes
d p 1 [ i ] [ s i z [ i ] − 1 ] ← d p 0 [ i ] [ 0 ] ⋅ ( [ i = f a [ x ] ∨ l c a ( i , x ) ≠ i ] + [ l c a ( i , x ) ≠ i ] ) dp1[i][siz[i]-1]\leftarrow dp0[i][0]\cdot([i=fa[x]\lor lca(i,x)\not=i]+[lca(i,x)\not=i]) dp1[i][siz[i]−1]←dp0[i][0]⋅([i=fa[x]∨lca(i,x)=i]+[lca(i,x)=i])
Finally, consider x x x The matching of your son .
Total States O ( ∑ s i z [ i ] ) O(\sum siz[i]) O(∑siz[i]) , Transfer is a classic tree backpack , So the total time complexity O ( n 3 ) O(n^3) O(n3) .
CODE
Not very often , There is even a lot of waste code
#include<map>
#include<set>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<random>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_map>
#pragma GCC optimize(2)
using namespace std;
#define MAXN 205
#define LL long long
#define ULL unsigned long long
#define ENDL putchar('\n')
#define DB double
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second
#define PR pair<int,int>
#define UIN unsigned int
int xchar() {
static const int maxn = 1000000;
static char b[maxn];
static int pos = 0,len = 0;
if(pos == len) pos = 0,len = fread(b,1,maxn,stdin);
if(pos == len) return -1;
return b[pos ++];
}
// #define getchar() xchar()
inline LL read() {
LL f = 1,x = 0;int s = getchar();
while(s < '0' || s > '9') {
if(s<0)return -1;if(s=='-')f=-f;s = getchar();}
while(s >= '0' && s <= '9') {
x = (x<<1) + (x<<3) + (s^48);s = getchar();}
return f*x;
}
void putpos(LL x) {
if(!x)return ;putpos(x/10);putchar((x%10)^48);}
inline void putnum(LL x) {
if(!x) {
putchar('0');return ;}
if(x<0) putchar('-'),x = -x;
return putpos(x);
}
inline void AIput(LL x,int c) {
putnum(x);putchar(c);}
const int MOD = 1000000007;
int n,m,s,o,k;
int rt,C[MAXN<<1][MAXN<<1];
int hd[MAXN],nx[MAXN<<1],v[MAXN<<1],cne;
void ins(int x,int y) {
nx[++ cne] = hd[x]; v[cne] = y; hd[x] = cne;
}
int d[MAXN],fa[MAXN];
void dfs0(int x,int ff) {
d[x] = d[fa[x] = ff] + 1;
for(int i = hd[x];i;i = nx[i]) {
if(v[i] != ff) {
dfs0(v[i],x);
}
}return ;
}
int lca(int a,int b) {
if(d[a] < d[b]) swap(a,b);
while(d[a] > d[b]) a = fa[a];
if(a == b) return a;
while(a != b) a = fa[a],b = fa[b];
return a;
}
int Ft;
int dp[MAXN][MAXN],dp1[MAXN][MAXN],siz[MAXN];
bool ifa[MAXN],mg[MAXN];
void dfsi(int x,int ff) {
dp[x][0] = 1; siz[x] = 0;
for(int i = hd[x];i;i = nx[i]) {
int y = v[i]; if(y == ff) continue;
dfsi(y,x); siz[x] += siz[y];
dp[x][0] = dp[x][0] *1ll* dp[y][0] % MOD * C[siz[x]][siz[y]] % MOD;
} siz[x] ++; return ;
}
void dfs(int x,int ff) {
for(int i = 0;i <= n;i ++) dp[x][i] = dp1[x][i] = 0;
dp[x][0] = 1; siz[x] = 0;
for(int i = hd[x];i;i = nx[i]) {
int y = v[i]; if(y==ff || y==Ft) continue;
dfs(y,x); siz[x] += siz[y];
for(int i = siz[x];i >= 0;i --) {
int dpp = 0,dpp1 = 0;
for(int j = max(0,siz[y]-(siz[x]-i));j <= siz[y] && j <= i;j ++) {
(dpp += dp[x][i-j]*1ll*dp[y][j]%MOD * C[siz[x]-i][siz[y]-j] % MOD * C[i][j] % MOD) %= MOD;
if(i<siz[x]) (dpp1 += dp1[x][i-j]*1ll*dp[y][j]%MOD * C[siz[x]-i-1][siz[y]-j] % MOD * C[i][j] % MOD) %= MOD;
if(i<siz[x] && j<siz[y]) (dpp1 += dp[x][i-j]*1ll*dp1[y][j]%MOD * C[siz[x]-i-1][siz[y]-j-1] % MOD * C[i][j] % MOD) %= MOD;
}
dp[x][i] = dpp; dp1[x][i] = dpp1;
}
}
siz[x] ++;
if(!ifa[x]) dp[x][siz[x]] = dp[x][0];
if(mg[x] && (!ifa[x] || x == fa[Ft])) (dp1[x][siz[x]-1] += dp[x][0]) %= MOD;
if(mg[x] && !ifa[x]) (dp1[x][siz[x]-1] += dp[x][0]) %= MOD;
return ;
}
int solve(int s,int op) {
Ft = s;
for(int i = 1;i <= n;i ++) {
ifa[i] = mg[i] = 0;
if(op > 0) mg[i] = (i > s);
else mg[i] = (i < s);
}
int as = 0;
int p = s; while(p) ifa[p] = 1,p = fa[p];
dfsi(s,fa[s]);
int le = siz[s];
int as0 = 1,as1 = 0,sz = 0;
for(int i = hd[s];i;i = nx[i]) {
int y = v[i]; if(y == fa[s]) continue;
sz += siz[y];
as1 = as1 *1ll* dp[y][0] % MOD * C[sz-1][siz[y]] % MOD;
if(mg[y]) (as1 += as0 *1ll* dp[y][0] % MOD * C[sz-1][siz[y]-1] % MOD) %= MOD;
as0 = as0 *1ll* dp[y][0] % MOD * C[sz][siz[y]] % MOD;
}
if(rt != s) {
dfs(rt,0);
for(int i = 0;i <= siz[rt];i ++) {
(as += dp1[rt][i] *1ll* dp[s][0] % MOD * C[le-1+i][i] % MOD) %= MOD;
if(le>1) (as += dp[rt][i] *1ll* as1 % MOD * C[le-2+i][i] % MOD) %= MOD;
}
}
else as = as1;
return as;
}
int main() {
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
n = read(); rt = read();
for(int i = 1;i < n;i ++) {
s = read();o = read();
ins(s,o); ins(o,s);
}
dfs0(rt,0);
C[0][0] = 1;
for(int i = 1;i <= n;i ++) {
C[i][0] = C[i][i] = 1;
for(int j = 1;j < i;j ++) {
C[i][j] = (C[i-1][j-1] + C[i-1][j]) % MOD;
}
}
int ans = 0;
for(int i = 1;i <= n;i ++) {
int A = solve(i,-1),B = solve(i,1);
ans = (ans + (A +MOD- B) *1ll* i) % MOD;
}
AIput(ans,'\n');
return 0;
}
边栏推荐
- QEMU STM32 vscode debugging environment configuration
- Use indent to format code
- On boost circuit
- Explain task scheduling based on Cortex-M3 in detail (Part 1)
- Hardware 1 -- relationship between gain and magnification
- Example 008: 99 multiplication table
- Introduction of air gap, etc
- Compilation warning solution sorting in Quartus II
- Example 010: time to show
- [paper reading] the latest transfer ability in deep learning: a survey in 2022
猜你喜欢
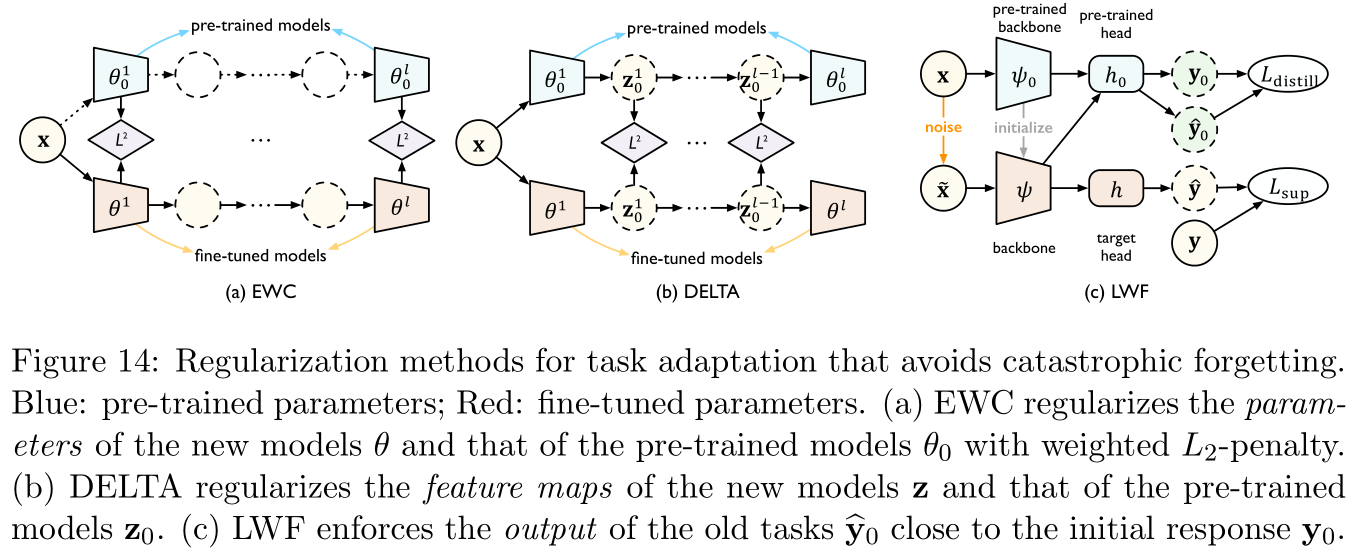
【论文阅读】2022年最新迁移学习综述笔注(Transferability in Deep Learning: A Survey)
![[nas1] (2021cvpr) attentivenas: improving neural architecture search via attentive sampling (unfinished)](/img/3b/c94b8466370f4461875c85b4f66860.png)
[nas1] (2021cvpr) attentivenas: improving neural architecture search via attentive sampling (unfinished)

Installation and use of libjpeg and ligpng
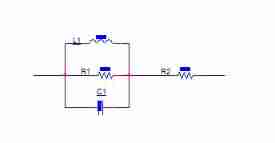
Talk about the function of magnetic beads in circuits
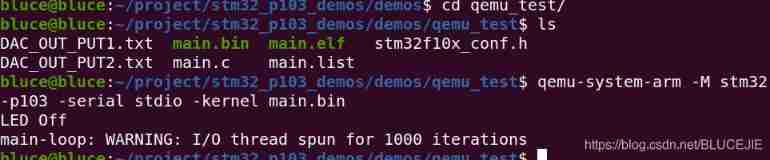
STM32 virtualization environment of QEMU

How to write cover letter?
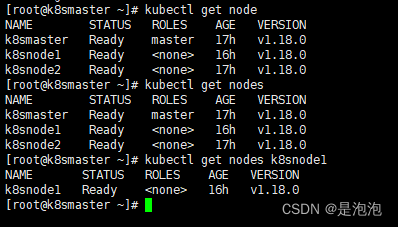
【云原生 | 从零开始学Kubernetes】三、Kubernetes集群管理工具kubectl
More than 90% of hardware engineers will encounter problems when MOS tubes are burned out!

Example 006: Fibonacci series

Management and use of DokuWiki
随机推荐
Classic application of MOS transistor circuit design (1) -iic bidirectional level shift
Google sitemap files for rails Projects - Google sitemap files for rails projects
The firmware of the connected j-link does not support the following memory access
实例003:完全平方数 一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
My-basic application 2: my-basic installation and operation
Example 005: three numbers sorting input three integers x, y, Z, please output these three numbers from small to large.
实例005:三数排序 输入三个整数x,y,z,请把这三个数由小到大输出。
Count the number of inputs (C language)
STM32---ADC
实例007:copy 将一个列表的数据复制到另一个列表中。
Infected Tree(树形dp)
STM32 single chip microcomputer -- debug in keil5 cannot enter the main function
STM32---IIC
STM32 single chip microcomputer - bit band operation
General makefile (I) single C language compilation template
Explication de la procédure stockée pour SQL Server
Semiconductor devices (I) PN junction
Anonymous structure in C language
Sql Server的存储过程详解
STM32 outputs 1PPS with adjustable phase