当前位置:网站首页>SDNU_ ACM_ ICPC_ 2022_ Summer_ Practice(1~2)
SDNU_ ACM_ ICPC_ 2022_ Summer_ Practice(1~2)
2022-07-08 00:38:00 【_ dawn°】
Catalog
P8346 「Wdoi-6」 The clearest air and sea ( A topological sort )
P8347 「Wdoi-6」 The moon on the other side ( game )
P8348 「Wdoi-6」 Unknown flower charm journey of knowledge ( thinking , mathematics )
P8319 『JROI-4』 fraction ( mathematics , law )
P8320 『JROI-4』Sunset( Two points )
P8321 『JROI-4』 Shenyang Street 2(DP, thinking , Inverse element )
P8346 「Wdoi-6」 The clearest air and sea ( A topological sort )
Original title transmission gate

Ideas : Because the condition is a perfect match, just 1, Let's first discuss it in categories :1、 Greater than 2 when , At this time, we can try to draw more pictures , It must be that the degree of each point is greater than or equal to 2, This is a good judgment ;2、 be equal to 1 when , Like the example , We find that when there is only one perfect match, the degree of existence must be 1 The point of ;3、 non-existent , We can draw a picture , Image situation 2 equally , The degree of existence must also be 1 The point of , for example :
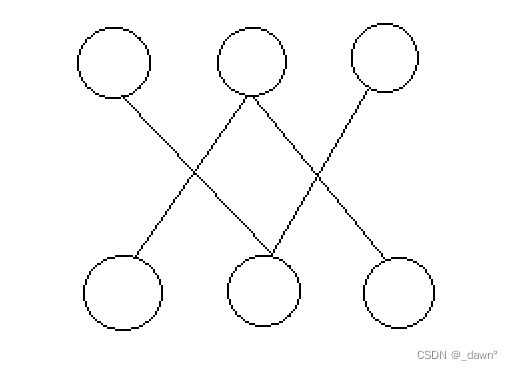
For three cases , In the first case, we can directly count the degree of each point ; In the second and third cases, we can use topological sorting to distinguish , Calculate the points of joining and leaving the team , Judge whether it is equal to 2*n that will do .
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=1e6+5;
int t,n,m;
int cnt[N<<1],del[N<<1];
std::vector<int>vec[N<<1];
bool check(){
std::queue<int>q;
int cntt=0;
for(int i=1;i<2*n;i++){
if(cnt[i]==1) q.push(i);
}
while(!q.empty()){
int now=q.front(),nex=0;
q.pop();
if(del[now]) continue;
del[now]=1,cntt++;
for(int i=0;i<vec[now].size();i++){
if(del[vec[now][i]]) continue;
nex=vec[now][i];
break;
}
del[nex]=1,cntt++;
for(int i=0;i<vec[nex].size();i++){
if(!del[vec[nex][i]]){
--cnt[vec[nex][i]];
if(cnt[vec[nex][i]]==1) q.push(vec[nex][i]);
}
}
}
if(cntt!=n*2) return false;
return true;
}
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while(t--){
std::cin>>n>>m;
for(int i=0;i<=n*2+3;i++){
vec[i].clear();
}
memset(cnt,0,sizeof(cnt));
memset(del,0,sizeof(del));
for(int i=1;i<=m;i++){
int u,v;
std::cin>>u>>v;
v+=n;
cnt[u]++,cnt[v]++;
vec[u].push_back(v);
vec[v].push_back(u);
}
bool flag=true;
for(int i=1;i<=(n<<1);i++){
if(cnt[i]<2){
flag=false;
break;
}
}
if(flag){
std::cout<<"Merry"<<'\n';
continue;
}
std::cout<<(check()?"Renko":"Merry")<<'\n';
}
return 0;
}
P8347 「Wdoi-6」 The moon on the other side ( game )
Original title transmission gate

Ideas : Conclusion game problem , You can start with a simple situation : One point , The first step is to win ; At two o'clock , The second is the winner ; At three o'clock , If you line up, you will win first , Chrysanthemum map shows that the hindhand will win . Analyze these simple examples , Find the conclusion : If there are even degree points , First hand wins , On the contrary, the backhand will win , The following proof :
We can set N The states are all odd degrees ,P The state is that there is an even degree , According to game theory , We just need to prove that the situation is P and N Alternate . First of all, we can find that the operation in the topic is to choose an edge to cut , The subsequent state is one of the subtrees after cutting . about N state , We assume that the cut edge is a connection u and v The edge of , Because of the original tree u,v The degrees of are all odd , So after cutting u,v The degrees of are even , At this point, no matter which side of the subtree is selected, there is a point with an even degree ; about P state , Because at most only a limited number of points have even degrees , Therefore, after arbitrarily determining a root, there must be a subtree in which only the degree of the root node is even , At this time, select this subtree as the successor state , That is to say N state .
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=1e5+5;
int t,n,u,v;
int cnt[N];
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while(t--){
std::cin>>n;
memset(cnt,0,sizeof(cnt));
for(int i=1;i<n;i++){
std::cin>>u>>v;
cnt[u]++,cnt[v]++;
}
bool flag=false;
for(int i=1;i<=n;i++){
if(!(cnt[i]&1)){
flag=true;
break;
}
}
std::cout<<(flag?"Hifuu":"Luna")<<'\n';
}
return 0;
}
P8348 「Wdoi-6」 Unknown flower charm journey of knowledge ( thinking , mathematics )
Original title transmission gate

Ideas : First, the four numbers specially awarded are less than k The situation of . To meet the requirements of the topic , We construct the array directly in some way so that a0,a1 become x,y Is not desirable , Because the data range is too large , So we can consider using some construction method to make these two logarithms construct the same logarithm . Meeting the conditions is actually very simple , But if you add it all the way , The final value is too large to handle , So you can use addition and subtraction , Such a set of data meets the conditions :x,y,x+y,x,y,x+y...... We can find that one addition can be offset by two subtractions , It has no effect on the answer , So we can always subtract , Until you can't continue to reduce , Judge whether the corresponding numbers of two logarithms are equal . Note that subtraction should be handled quickly by multiplication and division , Direct addition and subtraction will TLE.
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=1e5+5;
int t,a,b,x,y,k;
void work(int &x,int &y){
while(1){
if(x<y){
int now=(y-k)/x;
if(!now) break;
y-=now*x;
if(now&1) std::swap(x,y);
}
else if(x>y){
int now=(x-k)/y;
if(!now) break;
x-=now*y;
if(now&1) std::swap(x,y);
}
else break;
}
}
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while(t--){
std::cin>>a>>b>>x>>y>>k;
if(k>a||k>b||k>x||k>y){
std::cout<<"no"<<'\n';
continue;
}
work(a,b);
work(x,y);
if(a!=x||b!=y) std::cout<<"no"<<'\n';
else std::cout<<"yes"<<'\n';
}
return 0;
}
P8319 『JROI-4』 fraction ( mathematics , law )
Original title transmission gate

Ideas : Although it was made during the game, it was still written . The problem surface was misunderstood at the beginning , I think a sentence should be added , Reduce to the simplest , The reduction of points does not count the number of operations . You can know by writing a few examples by yourself , When the number of fractions is the least , The more operations , For a number , Obviously, when it is a prime number, the answer is equal to itself , In this way, the problem is transformed into finding the maximum prime number less than or equal to the given number . Sift the string , Two points to find the answer , Of course, it can also be pretreated directly ,O(1) Inquire about .
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=2e6+5;
int t,n,tot;
int prime[N];
bool mark[N];
void oula(){
for(int i=2;i<=N-3;++i){
if(!mark[i])
prime[++tot]=i;
for(int j=1;j<=tot;++j){
if(i*prime[j]>N) break;
mark[i*prime[j]]=1;
if(i%prime[j]==0) break;
}
}
}
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
oula();
std::cin>>t;
while(t--){
std::cin>>n;
if(n==1){
std::cout<<1<<'\n';
continue;
}
int pos=std::lower_bound(prime+1,prime+1+tot,n)-prime;
if(prime[pos]!=n)
pos--;
std::cout<<prime[pos]<<'\n';
}
return 0;
}P8320 『JROI-4』Sunset( Two points )
Original title transmission gate

Ideas : Pay attention to understanding d The meaning of array , So we can find that d Arrays are ordered , The last one must be the largest number in the array . operation 2 Yes, it will a The number in is changed to 0, To modify at the same time d The value of the array , It's easy to think of , Change the value of a large number to 0 after , Then find the element smaller than this number . The way is to find every number d Where the array values differ , Because this position must be a The position of this number in the array . Let's look at the data range ,5500 Time to ask ,500 Number , Ask each number at most 11 Time , Need to use binary search .
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=505;
int t,n;
int a[N];
inline int getmax(){
std::cout<<"? 1 "<<n<<std::endl;
std::cout<<std::flush;
int g;scanf("%d",&g);
int l=1,r=n,mid,ans,tmp;
while (l<=r){
mid=(l+r)>>1;
std::cout<<"? 1 "<<mid<<std::endl;
std::cout<<std::flush;
std::cin>>tmp;
if (tmp==g){
ans=mid;
r=mid-1;
}
else l=mid+1;
}
return ans;
}
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while (t--){
std::cin>>n;
memset(a,0,sizeof(a));
for(int i=n;i>1;i--){
int k=getmax();
a[k]=i;
std::cout<<"? 2 "<<k<<std::endl;
std::cout<<std::flush;
}
for(int i=1;i<=n;i++){
if (a[i]==0) a[i]=1;
}
std::cout<<"!";
for(int i=1;i<=n;i++)
std::cout<<' '<<a[i];
std::cout<<std::endl;
std::cout<<std::flush;
}
return 0;
}P8321 『JROI-4』 Shenyang Street 2(DP, thinking , Inverse element )
Original title transmission gate

Ideas : It seems that the requirements are frightening , But we can extract the model . We can see that a Array and b Combine numbers ,a The number of arrays is marked in red ,b The number sign of the array is blue , Select n The sum of the latter in the red blue pairing ( Look at the analysis of the big guy in Luogu , Have a good understanding of , It's really wonderful ) consider DP solve , hypothesis f[i][j] Express c[1,i] It's paired j Number of projects .
Transfer equation :f[i][j]=f[i−1][j−1]×c[i]×(tmp−(j−1))+f[i−1][j]
here tmp yes c[1,i-1] China and c[i] The number of different colors , stay DP Pretreatment before process cnt Array , Before calculation i The number of elements belonging to the red and blue array .
For the final answer , Because there is a 1/n!, Here are modulo operations , So we need to use Fermat's theorem to find the inverse element to get the answer .
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=998244353;
const int N=5e3+5;
ll n,a,b;
ll f[N<<1][N];
int cnt[2][N<<1];
struct node{
ll val;
ll belong;
bool operator <(const node &a) const{
return val>a.val;
}
} e[N<<1];
ll pmod(ll a,ll b){
ll res=1;
while(b){
if(b&1) res=res*a%mod;
b>>=1;
a=a*a%mod;
}
return res;
}
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>n;
for(int i=1;i<=n;i++){
std::cin>>a;
e[i].val=a,e[i].belong=0;
}
for(int i=1;i<=n;i++){
std::cin>>b;
e[i+n].val=b,e[i+n].belong=1;
}
std::sort(e+1,e+1+n*2);
for(int i=1;i<=2*n;i++){
cnt[0][i]=cnt[0][i-1];
cnt[1][i]=cnt[1][i-1];
cnt[e[i].belong][i]++;
}
f[0][0]=1;
for(ll i=1;i<=2*n;i++){
ll tmp=cnt[!e[i].belong][i];
f[i][0]=1;
for(ll j=1;j<=std::min(n,i);j++){
if(j<=tmp)
f[i][j]=f[i-1][j-1]*e[i].val%mod*(tmp-(j-1))%mod;
f[i][j]=(f[i-1][j]+f[i][j])%mod;
}
}
ll res=1;
for(int i=1;i<=n;i++){
res=res*i%mod;
}
std::cout<<pmod(res,mod-2)*f[2*n][n]%mod;
return 0;
}os: The second training match seems to be a monthly match in Los Angeles ,, After reading the last two questions , What kind of number theory field is this , It can't be mended , Convolution or something has not been touched yet (
If there is any mistake, please advise , thank you !
边栏推荐
- Huawei switch s5735s-l24t4s-qa2 cannot be remotely accessed by telnet
- paddle一个由三个卷积层组成的网络完成cifar10数据集的图像分类任务
- 2022-07-07:原本数组中都是大于0、小于等于k的数字,是一个单调不减的数组, 其中可能有相等的数字,总体趋势是递增的。 但是其中有些位置的数被替换成了0,我们需要求出所有的把0替换的方案数量:
- Prompt configure: error: required tool not found: libtool solution when configuring and installing crosstool ng tool
- What is load balancing? How does DNS achieve load balancing?
- 韦东山第三期课程内容概要
- DNS 系列(一):为什么更新了 DNS 记录不生效?
- Flask learning record 000: error summary
- 攻防世界Web进阶区unserialize3题解
- A brief history of information by James Gleick
猜你喜欢
应用实践 | 数仓体系效率全面提升!同程数科基于 Apache Doris 的数据仓库建设

取消select的默认样式的向下箭头和设置select默认字样
1293_FreeRTOS中xTaskResumeAll()接口的实现分析
赞!idea 如何单窗口打开多个项目?
“一个优秀程序员可抵五个普通程序员”,差距就在这7个关键点

备库一直有延迟,查看mrp为wait_for_log,重启mrp后为apply_log但过一会又wait_for_log

STM32F1與STM32CubeIDE編程實例-旋轉編碼器驅動
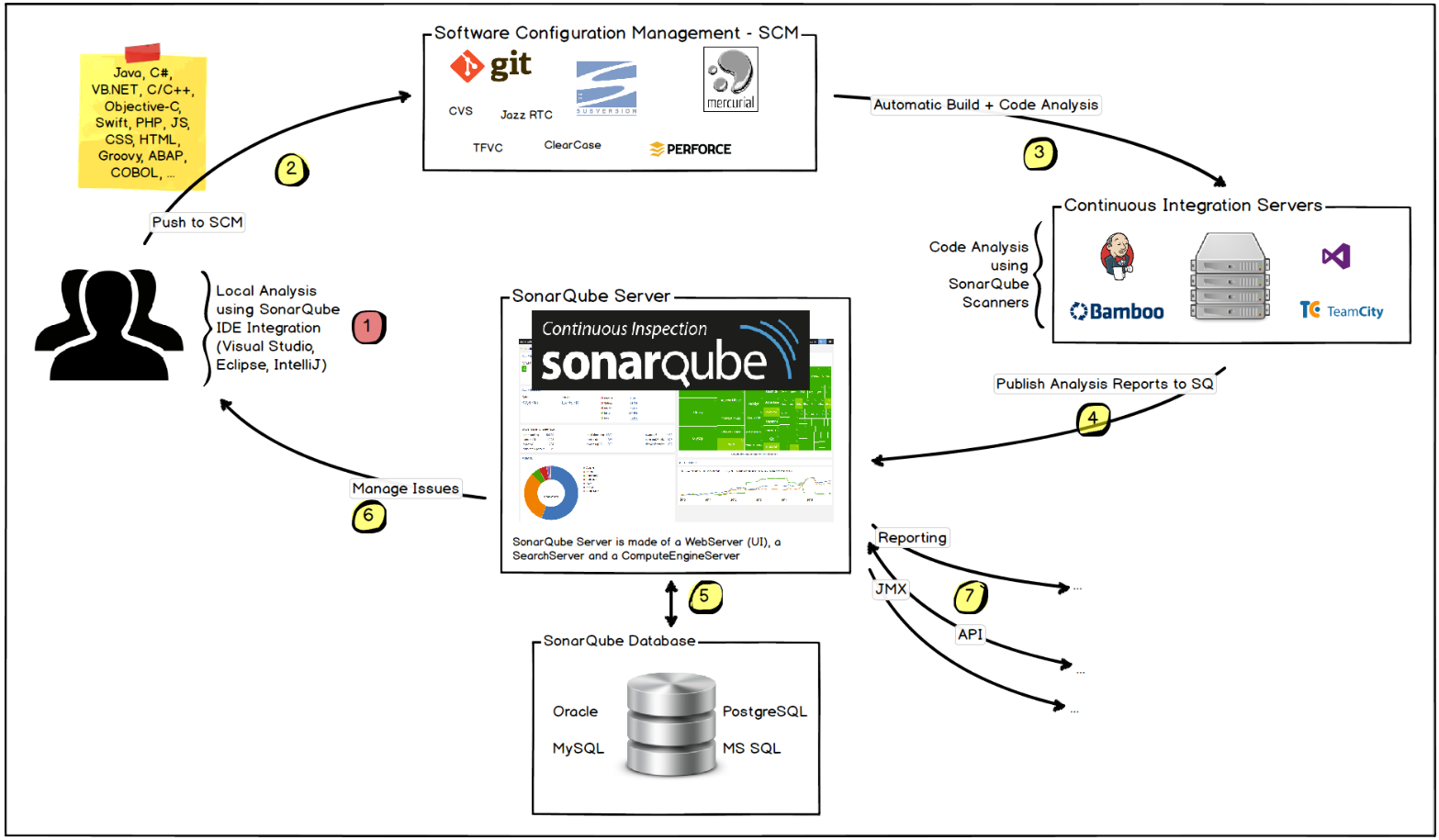
玩转Sonar
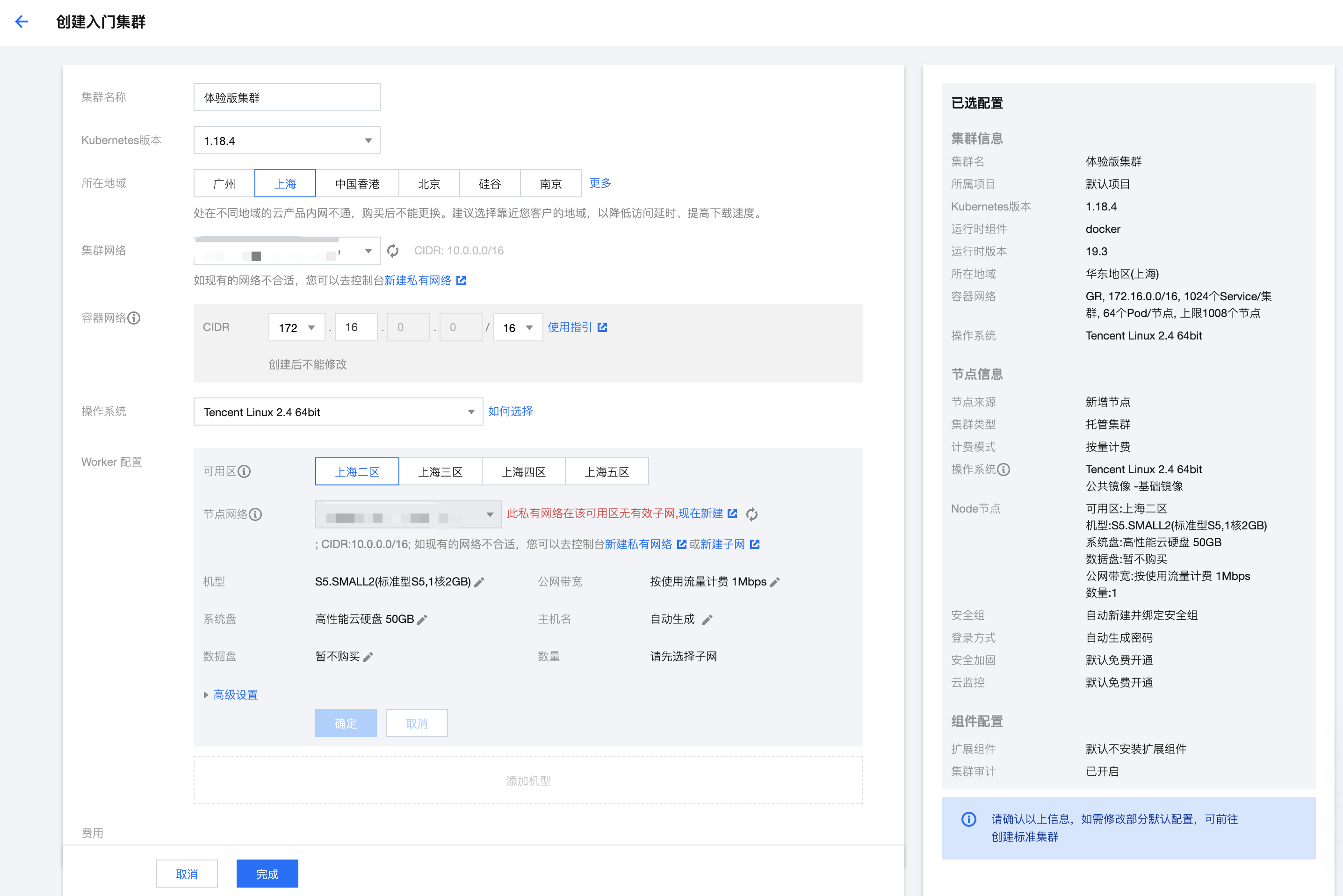
What has happened from server to cloud hosting?

Cancel the down arrow of the default style of select and set the default word of select
随机推荐
语义分割模型库segmentation_models_pytorch的详细使用介绍
华为交换机S5735S-L24T4S-QA2无法telnet远程访问
服务器防御DDOS的方法,杭州高防IP段103.219.39.x
【笔记】常见组合滤波电路
Prompt configure: error: required tool not found: libtool solution when configuring and installing crosstool ng tool
What has happened from server to cloud hosting?
大数据开源项目,一站式全自动化全生命周期运维管家ChengYing(承影)走向何方?
从服务器到云托管,到底经历了什么?
Deep dive kotlin synergy (XXII): flow treatment
They gathered at the 2022 ecug con just for "China's technological power"
Reading notes 004: Wang Yangming's quotations
Reentrantlock fair lock source code Chapter 0
DNS 系列(一):为什么更新了 DNS 记录不生效?
Trust orbtk development issues 2022
Deep dive kotlin collaboration (the end of 23): sharedflow and stateflow
tourist的NTT模板
丸子官网小程序配置教程来了(附详细步骤)
22年秋招心得
Basic mode of service mesh
Thinkphp内核工单系统源码商业开源版 多用户+多客服+短信+邮件通知