当前位置:网站首页>Hands on deep learning pytorch version exercise solution - 3.1 linear regression
Hands on deep learning pytorch version exercise solution - 3.1 linear regression
2022-07-03 10:20:00 【Innocent^_^】
The first question and the third question are open questions , There are many angles to think and answer . I hope this reference can help you in your study , Your correction is also of great benefit to me .
- Suppose we have ⼀ Some data x1, . . . , xn ∈ R. our ⽬ Mark is to find ⼀ It's a constant b, Minimize ∑ i ( x i − b ) 2 \sum_{i}(x_i-b)^2 ∑i(xi−b)2
(1) Find the best value b The analytic solution of .
(2) What is the relationship between this problem and its solution and normal distribution ? 2. Derive the envoy ⽤ flat ⽅ Analytical solution of linear regression optimization problem of error . To simplify the problem , The offset can be ignored b( We can go to X Add all values to 1 Of ⼀ Column to do this ⼀ spot ).
2. Derive the envoy ⽤ flat ⽅ Analytical solution of linear regression optimization problem of error . To simplify the problem , The offset can be ignored b( We can go to X Add all values to 1 Of ⼀ Column to do this ⼀ spot ).
(1)⽤ Matrix and vector table ⽰ Can't write optimization problems ( Treat all data as a single matrix , Will all ⽬ The scalar value is treated as a single vector )
(2) Calculate loss pair w Gradient of .
(3) By setting the gradient to 0、 Solving the matrix ⽅ To find the analytical solution .
(4) When might ⽐ send ⽤ Random gradient descent is better ? such ⽅ When will the law expire ? 3. It is assumed that additional noise is controlled ϵ The noise model is exponential distribution . in other words , p ( ϵ ) = 1 2 e x p ( − ∣ ϵ ∣ ) p(\epsilon)=\frac{1}{2}exp(-|\epsilon|) p(ϵ)=21exp(−∣ϵ∣)
3. It is assumed that additional noise is controlled ϵ The noise model is exponential distribution . in other words , p ( ϵ ) = 1 2 e x p ( − ∣ ϵ ∣ ) p(\epsilon)=\frac{1}{2}exp(-|\epsilon|) p(ϵ)=21exp(−∣ϵ∣)
\qquad (1) Write the model − l o g P ( y ∣ X ) −log P(y|X) −logP(y∣X) The negative log likelihood of the data
\qquad Explain : set up w = ( b , w 1 , … , w n ) , x i = ( 1 , x i 1 , … , x i n ) w=(b,w_1,\dots,w_n),x_i=(1,x_{i1},\dots,x_{in}) w=(b,w1,…,wn),xi=(1,xi1,…,xin).
be P ( y i ∣ x i ) = 1 2 e − ∣ y i − w x i ∣ ⇒ − l o g ∏ i = 1 n P ( y i ∣ x i ) = − ∑ i = 1 n l o g 1 2 e − ∣ y i − w x i ∣ P(y_i|x_i)=\frac{1}{2}e^{-|y_i-wx_i|} \Rightarrow -log\prod_{i=1}^{n}P(y_i|x_i) = -\sum_{i=1}^{n}log\frac{1}{2}e^{-|y_i-wx_i|} P(yi∣xi)=21e−∣yi−wxi∣⇒−log∏i=1nP(yi∣xi)=−∑i=1nlog21e−∣yi−wxi∣
= − ∑ i = 1 n ( − ∣ y i − w x i ∣ + l o g 1 2 ) = n l o g 2 + ∑ i = 1 n ∣ y i − w x i ∣ \qquad \quad \ \, = -\sum_{i=1}^{n}(-|y_i-wx_i|+log\frac{1}{2})=nlog2+\sum_{i=1}^{n}|y_i-wx_i| =−∑i=1n(−∣yi−wxi∣+log21)=nlog2+∑i=1n∣yi−wxi∣
\qquad (2) Can you write an analytical solution ?
\qquad Explain : The optimization goal is to minimize − l o g P ( y ∣ X ) -logP(\textbf{y}|\textbf{X}) −logP(y∣X), That is, the above results , About w Only the one with absolute value behind , So the absolute value is 0 Is the analytical solution , namely : − ∑ i = 1 n ∣ y i − w x i ∣ = − ∑ i = 1 n ( y i − w x i ) = 0 -\sum_{i=1}^{n}|y_i-wx_i|=-\sum_{i=1}^{n}(y_i-wx_i)=0 −∑i=1n∣yi−wxi∣=−∑i=1n(yi−wxi)=0
If y It's about x One variable function of , So above w = y 1 + y 2 + ⋯ + y n x 1 + x 2 + ⋯ + x n w=\frac{y_1+y_2+\dots+y_n}{x_1+x_2+\dots+x_n} w=x1+x2+⋯+xny1+y2+⋯+yn. If it is a multivariate function , Need to be written − ∑ i = 1 n ( y i − w T x i ) = 0 -\sum_{i=1}^{n}(y_i-w^Tx_i)=0 −∑i=1n(yi−wTxi)=0, Then it needs to be solved Y − w T X = 0 Y-w^TX=0 Y−wTX=0, So we get w = ( Y X − 1 ) T w=(YX^{-1})^T w=(YX−1)T
\qquad (3) Put forward ⼀ A random gradient descent algorithm to solve this problem . which ⾥ Possible error ?( carry ⽰: When we keep updating parameters , It will be sent near the stagnation point ⽣ What circumstance ) Can you solve this problem ?
\qquad Explain : This function is not differentiable at zero . And near zero , This is L1-loss, After derivation, the result is w w w, May correspond to loss Very small, but the gradient is too large , In this way, it is easy to oscillate , It's not easy to converge . Consider changing the optimization goal to smoothL1-loss( Refer to the forum in the book “Yang_Liu” User on 10 month 21 Answer from Japan )
边栏推荐
- Leetcode-513:找树的左下角值
- Boston house price forecast (tensorflow2.9 practice)
- Replace the files under the folder with sed
- Modelcheckpoint auto save model
- 2021-11-11 standard thread library
- Leetcode-112:路径总和
- [LZY learning notes dive into deep learning] 3.5 image classification dataset fashion MNIST
- Leetcode-112: path sum
- 『快速入门electron』之实现窗口拖拽
- 2-program logic
猜你喜欢
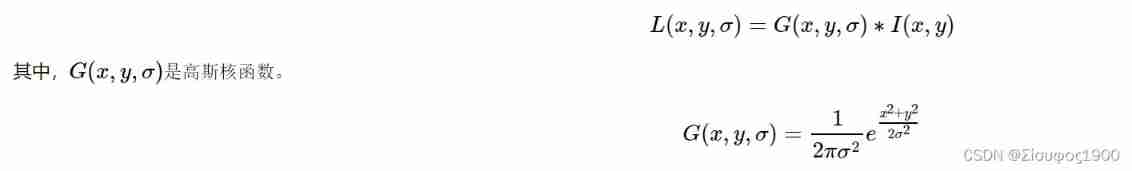
Opencv feature extraction sift
Anaconda安装包 报错packagesNotFoundError: The following packages are not available from current channels:

2312、卖木头块 | 面试官与狂徒张三的那些事(leetcode,附思维导图 + 全部解法)

Standard library header file

openCV+dlib實現給蒙娜麗莎換臉

使用密钥对的形式连接阿里云服务器
One click generate traffic password (exaggerated advertisement title)
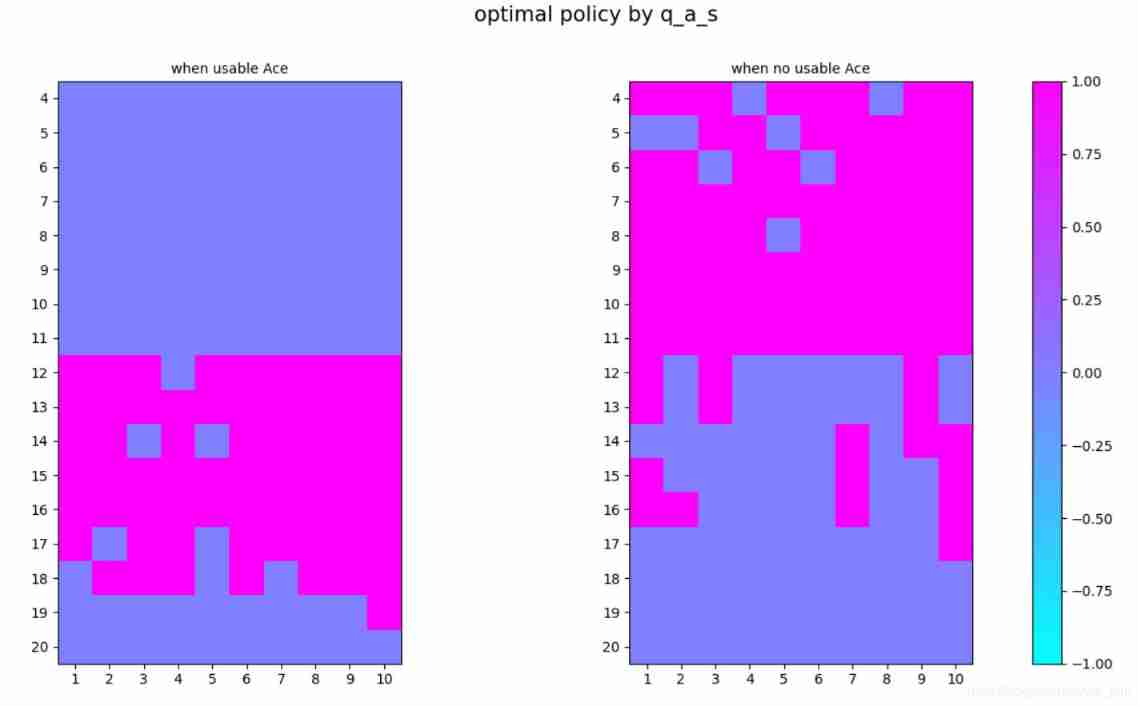
3.3 Monte Carlo Methods: case study: Blackjack of Policy Improvement of on- & off-policy Evaluation
Leetcode bit operation

Opencv image rotation
随机推荐
20220610其他:任务调度器
LeetCode - 715. Range module (TreeSet)*****
LeetCode - 1670 设计前中后队列(设计 - 两个双端队列)
Cases of OpenCV image enhancement
QT self drawing button with bubbles
2-program logic
When the reference is assigned to auto
Notes - regular expressions
LeetCode - 673. Number of longest increasing subsequences
Opencv feature extraction sift
Deep Reinforcement learning with PyTorch
Leetcode - 5 longest palindrome substring
Google browser plug-in recommendation
CV learning notes - reasoning and training
Neural Network Fundamentals (1)
CV learning notes - deep learning
Leetcode bit operation
4.1 Temporal Differential of one step
『快速入门electron』之实现窗口拖拽
Dynamic layout management