当前位置:网站首页>AI遮天传 ML-初识决策树
AI遮天传 ML-初识决策树
2022-07-07 23:10:00 【老师我作业忘带了】
决策树学习是最早被提出的一批机器学习的方法之一,由于它好用且具有很强的可解释性,到现在依然在被广泛使用。
一、决策树学习基础
(比较简单,一带而过)
例:享受一种运动

对于新的一天,是否可以去享受运动?
适用决策树学习的经典目标问题
- 带有非数值特征的分类问题
- 离散特征
- 没有相似度的
- 特征无序
另一个例子:水果
- 颜色:红色、绿色、黄色
- 大小:小、中、大
- 形状:球形、细长
- 味道:甜、酸
样本表示
属性的列表而非数值向量
例如享受运动的例子:
- 6值属性:天气、温度、湿度、风、水温、预测天气
- 某一天的天气实例:{晴、暖、一般、强、暖、不变}
例如水果的例子:
- 4值元组:颜色、大小、形状、味道
- 某个水果的实例: {红、球形、小、甜}
训练样本

决策树概念

决策树发展历史-里程碑
• 1966,由Hunt首先提出
• 1970’s~1980’s
• CART 由Friedman, Breiman提出
• ID3 由 Quinlan 提出
• 自1990’s以来
• 对比研究、算法改进(Mingers, Dietterich, Quinlan, etc.)
• 最广泛使用的决策树算法: C4.5 由 Quinlan 在 1993 年提
二、经典决策树算法 – ID3
自顶向下,贪心搜索
递归算法
核心循环:
- A :找出下一步 最佳 决策属性
- 将 A 作为当前节点决策属性
- 对属性A (vi )的每个值,创建与其对应的新的子节点
- 根据属性值将训练样本分配到各个节点
- 如果 训练样本被完美分类,则退出循环,否则进入递归状态继续向下探分裂新的叶节点

如:outlook是我们找出的最佳决策属性,我们就把它当成当前的根节点,根据outlook也就是天气情况我们就会有不同的分支不同的子节点,比如sunny、overcast、rain,如到了overcast就已经结束/有标签了,说明已经被分好了,如果还没被分好,我们就按照数据的取值把一批数据分到sunny、rain对应的分支上,humidity、wind,进入递归继续执行。如此时humidity是我们选择的最佳属性。
问题:
- 什么样的熟悉是最佳的决策属性?
- 什么叫做训练样本完美分类?
Q1:哪个属性是最佳属性?
比如这里有两个属性 A1(湿度)和 A2(风力)(64个数据,29个正例35个负例)

A1为true(湿度大)的有21正 5负 为false(湿度小)的有8正30负
A2为true(风力大)的有18正33负 为false(风力小)的有11正2负
注:正例是去运动,负例是不去。
此时到底A1和A2(湿度和风力)哪个作为根节点/最佳决策属性好呢?
当前最佳节点选择的基本原则:简洁
----我们偏向于使用简洁的具有较少节点的树

如上图,假如有两种水果,西瓜和柠檬。我们使用颜色color作为根节点则只需要根据green还是yellow便能够判断是西瓜还是柠檬。而如果我们选择size大小,大的肯定是西瓜了,而小的说不定还是小西瓜,所以还要根据颜色来判断。
属性选择和节点混杂度(Impurity)
属性选择的基本原则:简洁
—— 我们偏向于使用简洁的具有较少节点的树
在每个节点 N上,我们选择一个属性 T,使得到达当前派生节点的数据尽可能 “纯”
纯度(purity) – 混杂度(impurity)
如上图第一个的例子,经过了 颜色 ,则左边绿色都是西瓜右边黄色都是柠檬
而在第二个 尺寸 小 的节点上,又有西瓜又有柠檬,就不够 纯。
如何衡量混杂度?
1. 熵(Entropy) (广泛使用)


节点N的熵表示为在这个节点下不同的取值 (w:以size大小为例w1是大w2是小,
(w:以size大小为例w1是大w2是小, 为w1的概率,
为w1的概率, 为w2的概率。),每一个
为w2的概率。),每一个 的和的相反数。
的和的相反数。
- 定义: 0log0=0
- 在信息理论中,熵度量了信息的纯度/混杂度,或者信息的不确定性
- 由上图可知,熵最大的时候概率为一半一半,即此时最不确定。
- 正态分布 – 具有最大的熵值
计算并判断下图例子:

可以看到A1 A2都是29+,35-,接近一半一半,熵应该是接近于1的。


蓝线:1个类时概率为1,2个类时概率为0.5,16个类时概率为1/16
红线:1个类时最大熵为0,2个类时最大熵为1,无限增长。(其中最大时为均匀分布的)
2. Gini 混杂度 ( Duda 倾向于使用 Gini 混杂度)
在经济学和社会学上人们用 基尼系数 来衡量一个国家发展的平衡与否。

表示所有不相同情况的乘积(如果是A、B两种情况则p(A)*p(B),如果是A、B、C三种情况则p(A)*p(B)+p(A)*p(C)+p(B)*p(C))
或者 1-相同情况的乘积 ( )
)

n = number of class(也是因为是均匀分布的,各部分都是1/n)
有了上限,上限为1.
3. 错分类混杂度

1-最大类的概率,即1-大多数进入的那个类(分对了,1-就是错的)

度量混杂度的变化--信息增益(IG)
由于对A的排序整理带来的熵的期望减少量

原始S的熵值-经过属性A分类以后的期望熵值
 经计算,可见A1(湿度)的IG(信息增益)更大一些,也就意味着我们获得了更多的信息(减少的熵更多一些),我们选择A1作为根节点。
经计算,可见A1(湿度)的IG(信息增益)更大一些,也就意味着我们获得了更多的信息(减少的熵更多一些),我们选择A1作为根节点。
例:根据下表选择用哪个属性做根节点

Outlook的Gain最大,选它作为根节点。
Q2: 何时返回(停止分裂节点)?
“如果训练样本被完美分类”
• 情形 1: 如果当前子集中所有数据 有完全相同的输出类别,那么终止

• 情形 2: 如果当前子集中所有数据 有完全相同的输入特征,那么终止
比如:晴天-无风-湿度正常-温度合适,最后有的去了有的没去。此时即使不终止也没办法了,因为能用的信息已经用完了。这意味着:1、数据有噪声noise。需要进行清理,如果噪声过多说明数据质量不够好。2、漏掉了重要的Feature,比如漏掉了当天是否有课,有课就没办法出去玩。
可能的情形3: 如果 所有属性分裂的信息增益为0, 那么终止 这是个好想法吗?(No)

如上图此时树的第一个节点都找不出来(IG都是0),如果3说得对,那此时决策树都无法构建。
假如我们不要这个条件,反正都一样,IG都是0,多个最大值的时候随机选一个关系就被构建出来了(此时也完美分类了)

即在ID3中只有上面两种情况会停止分裂,如果IG=0,则随机取一个就好。
ID3算法搜索的假设空间

- 假设空间是完备的(即能处理属性的析取又能处理属性的合取)
目标函数一定在假设空间里
- 输出单个假设(沿着树的一条路走下去)
不超过20个问题(根据经验,一般feature不超过20个,过于复杂树比较长也容易产生过拟合)
- 没有回溯(以A1做根节点,没办法退回去看A2做根节点怎么样)
局部最优
- 在每一步中使用子集的所有数据(比如梯度下降算法里权值的更新策略是每条数据更新一次的话,那就是每次只使用一条数据)
数据驱动的搜索选择
对噪声数据有鲁棒性
ID3中的归纳偏置(Inductive Bias)
- 假设空间 H 是作用在样本集合 X 上的
没有对假设空间作限制
- 偏向于在靠近根节点处的属性具有更大信息增益的树
尝试找到最短的树
该算法的偏置在于对某些假设具有一些偏好 (搜索偏置), 而不是对假设空间 H 做限制(描述偏置).
奥卡姆剃刀(Occam’s Razor)*:偏向于符合数据的最短的假设
CART (分类和回归树)
一个通用的框架:
- 根据训练数据构建一棵决策树
- 决策树会逐渐把训练集合分成越来越小的子集
- 当子集纯净后不再分裂
- 或者接受一个不完美的决策
许多决策树算法都在这个框架下,包括ID3、C4.5等等。
三、过拟合问题

如上图,b比a更好,但如果像c一样每个点都被完美拟合了,错误率为0,但是如果有一个新的点:

此时c的算法的误差就太大了,过于匹配训练数据了,使得它在测试的更多未见实例上的泛化能力下降了。
决策树过拟合的一个极端例子:
- 每个叶节点都对应单个训练样本 —— 每个训练样本都被完美地分类
- 整个树相当于仅仅是一个数据查表算法的简单实现
即此时的树就是一个数据查表,可以类比数据结构里哈希表。这意味着查找时只能查找表里有的数据,对于没有的数据查不到,没什么泛化能力。

四、如何避免过拟合
对决策树来说有两种方法避免过拟合
- 当数据的分裂在统计意义上并不显著(如样例少)时,就停止增长:预剪枝
- 构建一棵完全树,然后再做后剪枝
在实际应用中,一般预剪枝更快, 而后剪枝得到的树准确率更高。
对于预剪枝
很难估计树的大小
预剪枝: 基于样本数
通常一个节点不再继续分裂,当:
- 到达一个节点的训练样本数小于训练集合的一个特定比例 (例如 5%)
- 无论混杂度或错误率是多少
- 原因:基于过少数据样本的决定会带来较大误差和泛化错误(盲人摸象)
比如有100个数据,到当前节点只有5个数据了,就不继续向下分了,无论几个正几个负,说明分的过细了。
预剪枝: 基于信息增益的阈值
- 设定一个较小的阈值,如果满足下述条件则停止分裂:
- 优点: 1. 用到了所有训练数据 2. 叶节点可能在树中的任何一层
- 缺点: 很难设定一个好的阈值
选IG大的为节点,如果IG最大的还是有点小了, 则停止。
则停止。
对于后剪枝:
• 如何选择 “最佳” 的树?
在另外的验证集合上测试效果
• MDL (Minimize Description Length 最小描述长度):
minimize ( size(tree) + size(misclassifications(tree)) ) 树的大小和错误率的和最小
后剪枝: 错误降低剪枝
• 把数据集分为训练集和验证集
• 验证集:
• 已知标签
• 测试效果
• 不要在验证集上不做模型更新!
• 剪枝直到再剪就会对损害性能:
• 在验证集上测试剪去每个可能节点(和以其为根的子树)的影响
• 贪心地去掉某个可以提升验证集准确率的节点
剪掉某个节点后,如何定义新的叶节点(父亲)的标签呢?
剪枝后新的叶节点的标签赋值策略
• 赋值成最常见的类别(60个data,50个+10个-,那就+)
• 给这个节点多类别的标签
每个类别有一个支持度(5/6:1/6) (根据训练集中每种标签的数目)
测试时: 依据概率(5/6:1/6)选择某个类别或选择多个标签
• 如果是一个回归树 (数值标签),可以做平均或加权平均
• ……
错误降低剪枝的效果

从后到前,在验证集上一点点减枝。
后剪枝: 规则后剪枝
1. 把树转换成等价的由规则构成的集合
• e.g. if (outlook=sunny)^ (humidity=high) then playTennis = no
2. 对每条规则进行剪枝,去除哪些能够提升该规则准确率的规则前件
• i.e. (outlook=sunny)60%, (humidity=high)85%,(outlook=sunny)^ (humidity=high)80%
3. 将规则排序成一个序列 (验证集:根据规则的准确率从高往低排序)
4. 用该序列中的最终规则对样本进行分类(依次查看是否满足规则序列,即在规则集合上一条一条往下走直到能判断出来)
(注:在规则被剪枝后,它可能不再能恢复成一棵树)
一种被广泛使用的方法,例如C4.5
为什么在剪枝前将决策树转化为规则?
• 独立于上下文
• 否则,如果子树被剪枝,有两个选择:
• 完全删除该节点
• 保留它
• 不区分根节点和叶节点
• 提升可读性
五、扩展: 现实场景中的决策树学习
1. 连续属性值

• 建立一些离散属性值,区间化,便于建立分支
• 可选的策略:
• I.选择相邻但有不同决策的值的中间值 
上图48与60,80与90之间yes no变了,我们可以取中间值
(Fayyad 在1991年证明了满足这样条件的阈值可以信息增益IG最大化)
• II. 考虑概率 
如正态分布概率密度函数图像,区间长短可以不同,但其面积/数量是相同的。
2. 具有过多取值的属性
问题:
• 偏差: 如果属性有很多值,根据信息增益IG,会优先被选择
• e.g. 享受运动的例子中,将一年里的每一天作为属性(又变成像查表了)
• 一个可能的解决方法: 用 GainRatio (增益比)来替代

3. 未知属性值

有的特征我们不知道是什么,可以把不知道的选成常见的,或者根据概率赋值。
4. 有代价的属性

即如果feature多,IG可以除以一个惩罚项,有代价可以除以cost...
六、其他信息
• 决策树可能是最简单和频繁使用的算法
• 易于理解
• 易于实现
• 易于使用
• 计算开销小
• 决策森林:
• 由C4.5产生的许多决策树
• 更新的算法:C5.0 http://www.rulequest.com/see5-info.html
• Ross Quinlan的主页: http://www.rulequest.com/Personal/
边栏推荐
- 【愚公系列】2022年7月 Go教学课程 006-自动推导类型和输入输出
- FOFA-攻防挑战记录
- 【obs】官方是配置USE_GPU_PRIORITY 效果为TRUE的
- A brief history of information by James Gleick
- Lecture 1: the entry node of the link in the linked list
- Stock account opening is free of charge. Is it safe to open an account on your mobile phone
- Password recovery vulnerability of foreign public testing
- Introduction to paddle - using lenet to realize image classification method I in MNIST
- 国外众测之密码找回漏洞
- 新库上线 | 中国记者信息数据
猜你喜欢
CVE-2022-28346:Django SQL注入漏洞
![[OBS] the official configuration is use_ GPU_ Priority effect is true](/img/df/772028e44776bd667e814989e8b09c.png)
[OBS] the official configuration is use_ GPU_ Priority effect is true
1293_ Implementation analysis of xtask resumeall() interface in FreeRTOS
Application practice | the efficiency of the data warehouse system has been comprehensively improved! Data warehouse construction based on Apache Doris in Tongcheng digital Department
大数据开源项目,一站式全自动化全生命周期运维管家ChengYing(承影)走向何方?
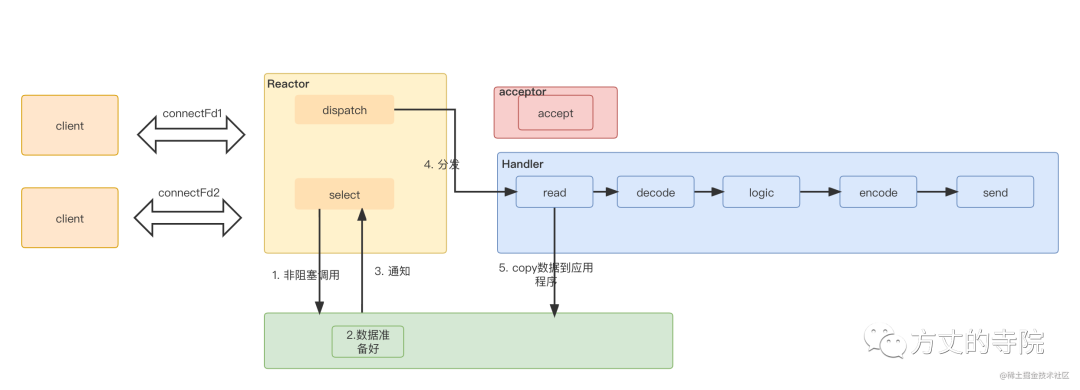
Single machine high concurrency model design
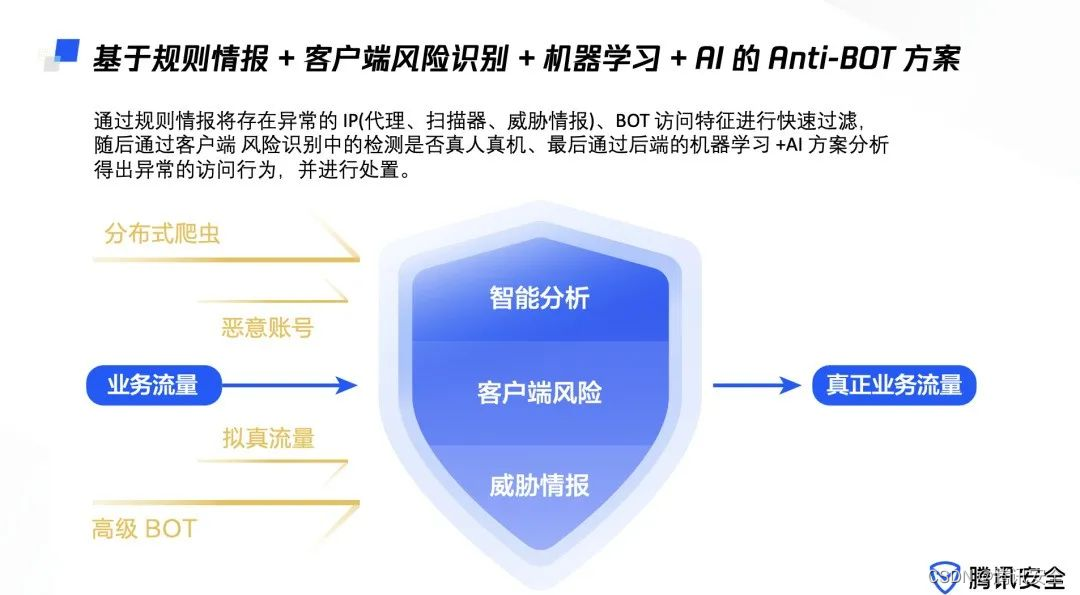
Tencent security released the white paper on BOT Management | interpreting BOT attacks and exploring ways to protect

3年经验,面试测试岗20K都拿不到了吗?这么坑?
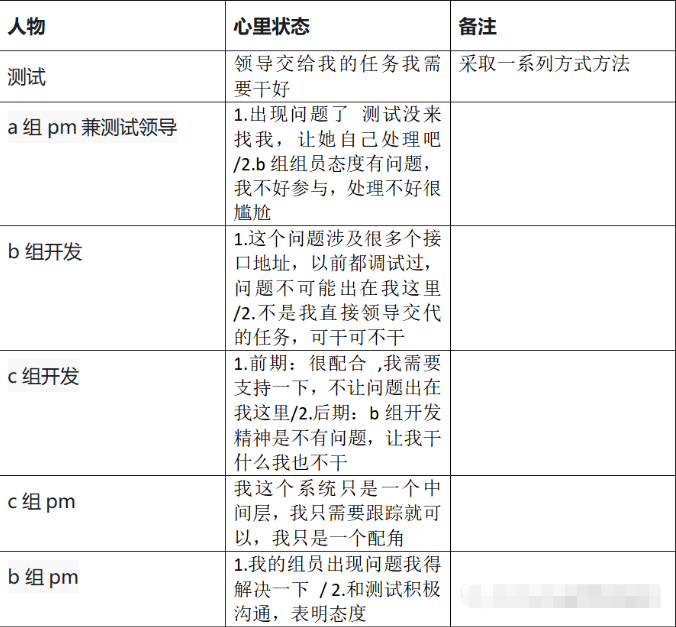
测试流程不完善,又遇到不积极的开发怎么办?
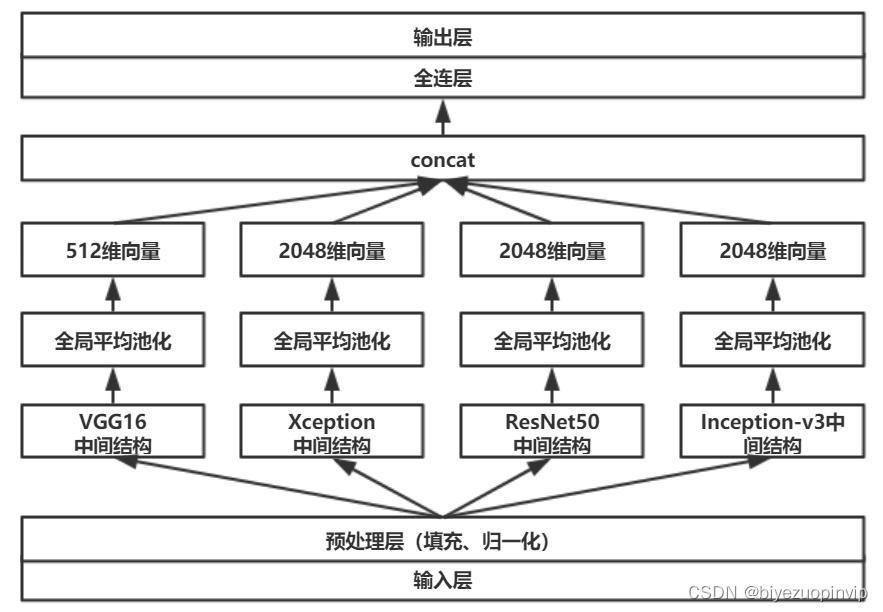
Malware detection method based on convolutional neural network
随机推荐
Summary of the third course of weidongshan
The method of server defense against DDoS, Hangzhou advanced anti DDoS IP section 103.219.39 x
Huawei switch s5735s-l24t4s-qa2 cannot be remotely accessed by telnet
Reptile practice (VIII): reptile expression pack
C # generics and performance comparison
[Yugong series] go teaching course 006 in July 2022 - automatic derivation of types and input and output
Solution to the problem of unserialize3 in the advanced web area of the attack and defense world
服务器防御DDOS的方法,杭州高防IP段103.219.39.x
攻防演练中沙盘推演的4个阶段
5g NR system messages
【obs】官方是配置USE_GPU_PRIORITY 效果为TRUE的
Is Zhou Hongyi, 52, still young?
基于人脸识别实现课堂抬头率检测
Binder核心API
手写一个模拟的ReentrantLock
【obs】Impossible to find entrance point CreateDirect3D11DeviceFromDXGIDevice
Sqlite数据库存储目录结构邻接表的实现2-目录树的构建
Malware detection method based on convolutional neural network
An error is reported during the process of setting up ADG. Rman-03009 ora-03113
詹姆斯·格雷克《信息简史》读后感记录