当前位置:网站首页>1855. Maximum distance of subscript alignment
1855. Maximum distance of subscript alignment
2022-07-06 16:08:00 【mrbone9】
Address :
Power button  https://leetcode-cn.com/problems/maximum-distance-between-a-pair-of-values/
https://leetcode-cn.com/problems/maximum-distance-between-a-pair-of-values/
subject :
Here are two for you Non-increasing Array of integers for nums1 and nums2 , Array subscripts are from 0 Start Count .
Subscript pair (i, j) in 0 <= i < nums1.length And 0 <= j < nums2.length . If the subscript pair satisfies both i <= j And nums1[i] <= nums2[j] , Call it It works Subscript pair , The subscript is right distance by j - i .
Back to all It works Subscript pair (i, j) Medium Maximum distance . If there is no valid subscript pair , return 0 .
An array arr , If each 1 <= i < arr.length Both arr[i-1] >= arr[i] establish , So the array is a Non-increasing Array .
Example 1:
| Input :nums1 = [55,30,5,4,2], nums2 = [100,20,10,10,5] Output :2 explain : The valid subscript pair is (0,0), (2,2), (2,3), (2,4), (3,3), (3,4) and (4,4) . The maximum distance is 2 , Corresponding subscript pair (2,4) . |
Example 2:
| Input :nums1 = [2,2,2], nums2 = [10,10,1] Output :1 explain : The valid subscript pair is (0,0), (0,1) and (1,1) . The maximum distance is 1 , Corresponding subscript pair (0,1) . |
Example 3:
| Input :nums1 = [30,29,19,5], nums2 = [25,25,25,25,25] Output :2 explain : The valid subscript pair is (2,2), (2,3), (2,4), (3,3) and (3,4) . The maximum distance is 2 , Corresponding subscript pair (2,4) . |
Example 4:
| Input :nums1 = [5,4], nums2 = [3,2] Output :0 explain : There is no valid subscript pair , So back 0 . |
Tips :
| 1 <= nums1.length <= 105 1 <= nums2.length <= 105 1 <= nums1[i], nums2[j] <= 105 nums1 and nums2 All are Non-increasing Array |
source : Power button (LeetCode)
link :https://leetcode-cn.com/problems/maximum-distance-between-a-pair-of-values
Copyright belongs to the network . For commercial reprint, please contact the official authority , Non-commercial reprint please indicate the source .
Ideas :
For a non increasing array , It means that the value of array elements is decreasing
Traverse the array according to the meaning of the question 1 Every element of , And array 2 Compare the elements of , Find the maximum distance
To reduce the number of comparisons , From the array 2 Compare the last element of , This is the longest distance , If it doesn't , Then compare the second
Such a violent solution is bound to timeout , The code is posted below
Since violence doesn't work, we have to think of other ways
Because it is a comparative distance , Array values are not directly related to distance , Therefore, two sets of data cannot be deduced , We can only compare
With i As Array 1 The subscript ,j As Array 2 The subscript
i from 0 Start , Initially found step ( Longest distance ) zero
[i] In the array 2 Look for the biggest place to exist , The last one [i] <= [j], Set up step = j - i
first i When the element is complete , We found the step size
The next element i+1 The element benchmarking is j+1 The location of ,
There may be [i+1] == [j+1] , A distance of 0, It won't be longer than the last time , So don't consider
May also be [i+1] <= [j+n],j After a certain step n In the back . This address is where we start to compare , therefore
The step length we found in the first step is used as a new starting point , If a new starting point [j] > [i], We will continue to try j Move back to find a new step
Such a calculation step can effectively reduce the number of comparisons
Method 1 、BF
int maxDistance(int* nums1, int nums1Size, int* nums2, int nums2Size){
int i, j;
int max = 0;
for(i=0; i<nums1Size; i++)
{
for(j=nums2Size-1; j>=0; j--)
{
if(nums1[i] <= nums2[j])
{
if(max < (j-i) )
max = j-i;
break;
}
}
}
return max;
}Method 2 、 Step comparison
int maxDistance(int* nums1, int nums1Size, int* nums2, int nums2Size){
int i, j;
int step = 0;
for(i=0; i<nums1Size; i++)
{
if(i+step < nums2Size && nums1[i] > nums2[i+step])
continue;
for(j=i+step; j<nums2Size; j++)
{
//printf("2..nums1[%d]=%d, nums2[%d]=%d\n", i, nums1[i], j, nums2[j]);
if(nums1[i] <= nums2[j])
{
step = j-i;
}
else
break;
}
}
return step;
}边栏推荐
- frida hook so层、protobuf 数据解析
- 【练习-3】(Uva 442)Matrix Chain Multiplication(矩阵链乘)
- Nodejs+vue网上鲜花店销售信息系统express+mysql
- 【练习-7】Crossword Answers
- Opencv learning log 28 -- detect the red cup cover
- 信息安全-安全专业名称|CVE|RCE|POC|VUL|0DAY
- 【练习-9】Zombie’s Treasure Chest
- TCP's three handshakes and four waves
- CS zero foundation introductory learning record
- 信息安全-威胁检测-NAT日志接入威胁检测平台详细设计
猜你喜欢
Write web games in C language
Pyside6 signal, slot
Frida hook so layer, protobuf data analysis
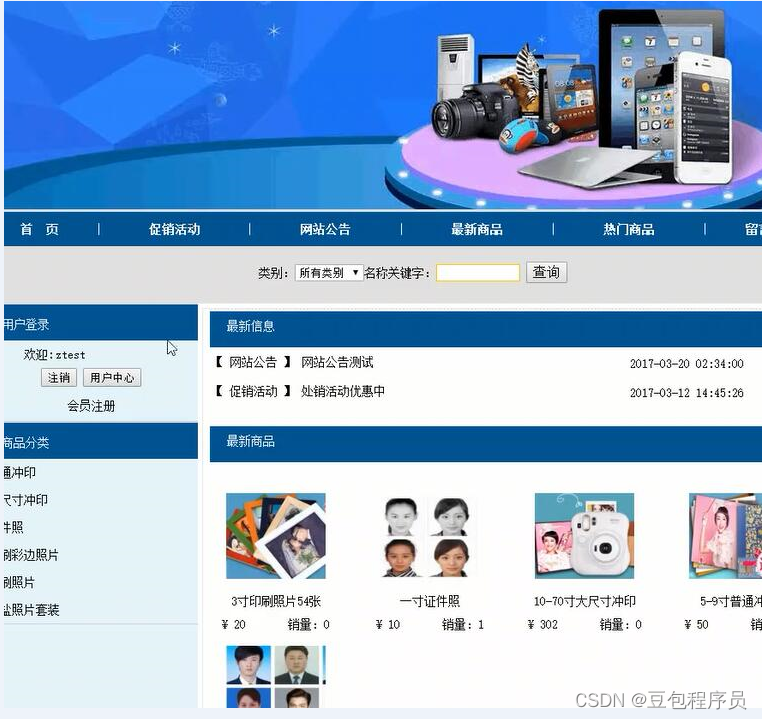
基于web的照片数码冲印网站

信息安全-史诗级漏洞Log4j的漏洞机理和防范措施
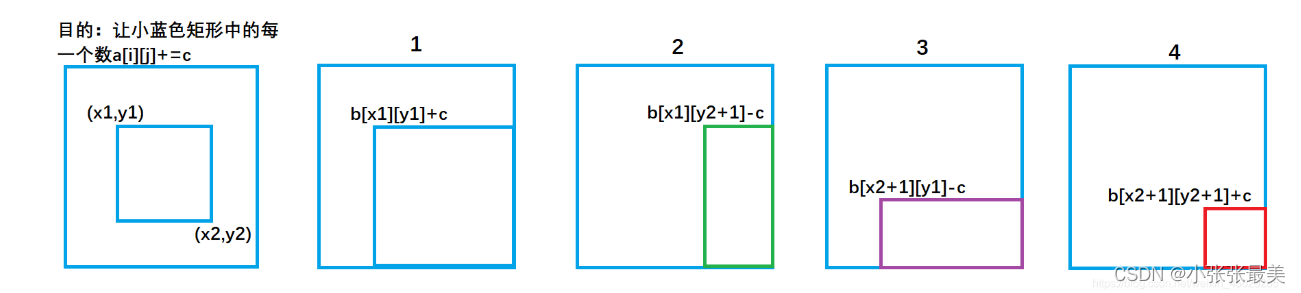
Differential (one-dimensional, two-dimensional, three-dimensional) Blue Bridge Cup three body attack
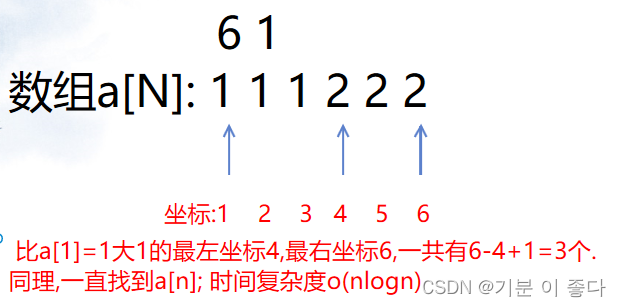
Luogu P1102 A-B number pair (dichotomy, map, double pointer)
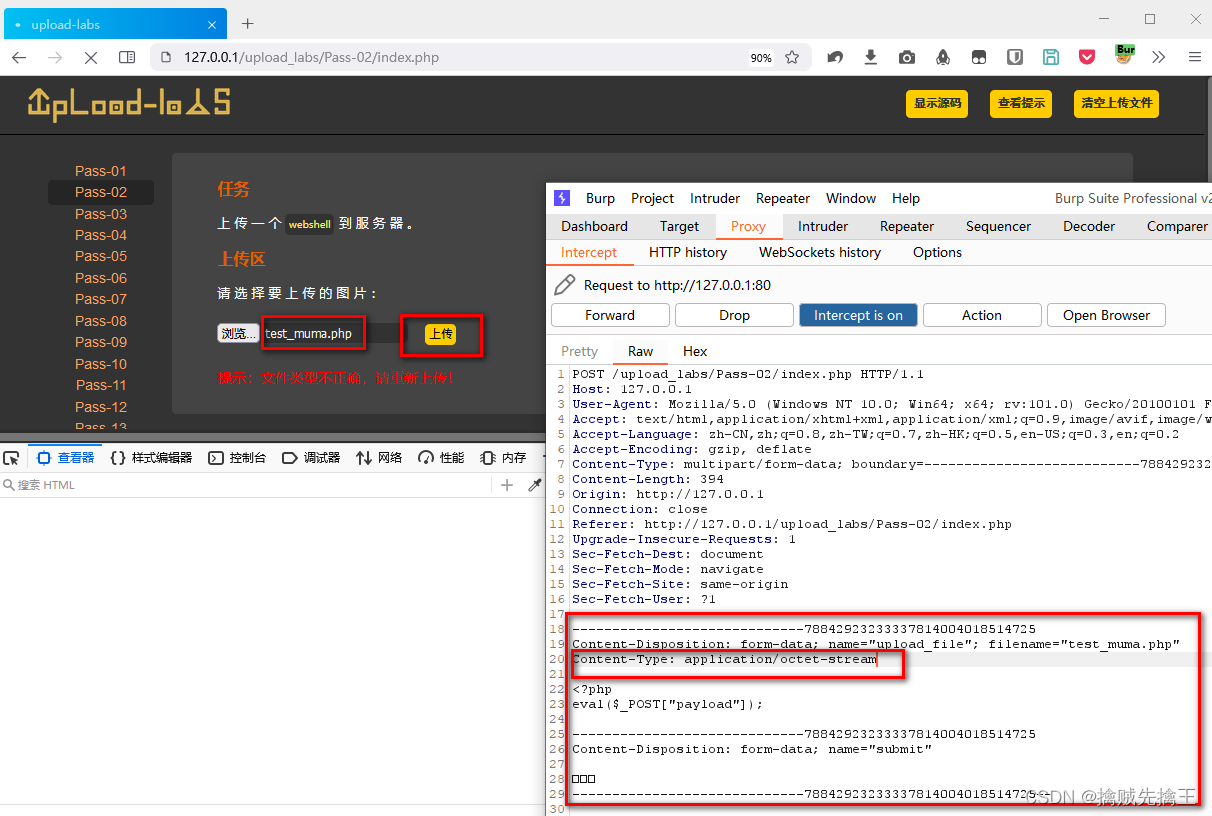
Penetration test 2 --- XSS, CSRF, file upload, file inclusion, deserialization vulnerability
渗透测试 ( 3 ) --- Metasploit Framework ( MSF )
frida hook so层、protobuf 数据解析
随机推荐
B - Code Party (girls' competition)
Information security - threat detection - detailed design of NAT log access threat detection platform
Ball Dropping
树莓派CSI/USB摄像头使用mjpg实现网页摄像头监控
Opencv learning log 15 count the number of solder joints and output
Penetration test (1) -- necessary tools, navigation
Research Report on surgical fluid treatment industry - market status analysis and development prospect prediction
What is the difficulty of programming?
Opencv learning log 32 edge extraction
B - 代码派对(女生赛)
【练习4-1】Cake Distribution(分配蛋糕)
Opencv learning log 26 -- detect circular holes and mark them
1323. Maximum number of 6 and 9
Auto. Getting started with JS
Essai de pénétration (1) - - outils nécessaires, navigation
Ball Dropping
Differential (one-dimensional, two-dimensional, three-dimensional) Blue Bridge Cup three body attack
C basic grammar
Gartner: five suggestions on best practices for zero trust network access
Information security - security professional name | CVE | rce | POC | Vul | 0day