Ball Dropping

Ball Dropping

Topic link ：https://ac.nowcoder.com/acm/contest/11166/B
source ： Cattle from

A standard sphere ball is falling in the air, and the center of the sphere is exactly on the centerline of an empty isosceles trapezoidal. The trapezoid is hanging horizontally under the sphere.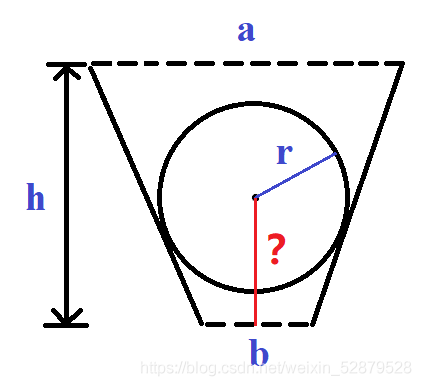

Please determine whether the ball will get stuck in the trapezoid or drop past the trapezoid.
Input description :
The input contains four integers r,a,b,h(1≤r,a,b,h≤1000,a>b), indicating the radius of the ball, the top base, the bottom base, and the height of the isosceles trapezoid.

It is guaranteed that 2r !=b,2r<a,2r<h.
Output description :
Output ‘Drop’ if the sphere ball will drop past the empty trapezoid, otherwise output ‘Stuck’.
If the answer is ‘Stuck’, please also calculate the stuck position(the height between the center of the sphere and the midpoint of the bottom base). Your answer is considered correct if its absolute or relative error does not exceed 10^−6

Example 1
Input
2 8 2 5
Output
Stuck
2.2206345966
Example 2
Input
1 8 3 5
Output
Drop

Very simple sign in question ;

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<stack>
#include<set>
#include<vector>
#include<map>
#include<queue>
using namespace std;
typedef long long ll;
double n,m,u,v,b,a,ma=-1,r,h;
int main()
{
    
    cin>>r>>a>>b>>h;
    if(r*2<b)
        cout<<"Drop";
    else{
    
        cout<<"Stuck"<<endl;
        double u;
        u=(2.0*r*sqrt(h*h+(a-b)*(a-b)*1.0/4)-b*h)*1.0/(a-b);
        printf("%.10f",u);
    }
    return 0;
}