当前位置:网站首页>[exercise-2] (UVA 712) s-trees
[exercise-2] (UVA 712) s-trees
2022-07-06 15:56:00 【Flame car】
Don't want to see such a long problem stem, just skip , There is translation behind it …… In fact, this question is simply a few words , It takes so long to get dirty, hahaha .
S-Trees
Description
A Strange Tree (S-tree) over the variable set Xn={x1,x2,…,xn} is a binary tree representing a Boolean function f:{0,1}n→{0,1}. Each path of the S-tree begins at the root node and consists of n+1 nodes. Each of the S-tree’s nodes has a depth, which is the amount of nodes between itself and the root (so the root has depth 0). The nodes with depth less than n are called non-terminal nodes. All non-terminal nodes have two children: the right child and the left child. Each non-terminal node is marked with some variable xi from the variable set Xn. All non-terminal nodes with the same depth are marked with the same variable, and non-terminal nodes with different depth are marked with different variables. So, there is a unique variable xi1 corresponding to the root, a unique variable xi2 corresponding to the nodes with depth 1, and so on. The sequence of the variables xi1,xi2,…,xin is called the variable ordering. The nodes having depth n are called terminal nodes. They have no children and are marked with either 0 or 1. Note that the variable ordering and the distribution of 0’s and 1’s on terminal nodes are sufficient to completely describe an S-tree.
As stated earlier, each S-tree represents a Boolean function f. If you have an S-tree and values for the variables x1,x2,…,xn, then it is quite simple to find out what f(x1,x2,…,xn) is: start with the root. Now repeat the following: if the node you are at is labelled with a variable xi, then depending on whether the value of the variable is 1 or 0, you go its right or left child, respectively. Once you reach a terminal node, its label gives the value of the function.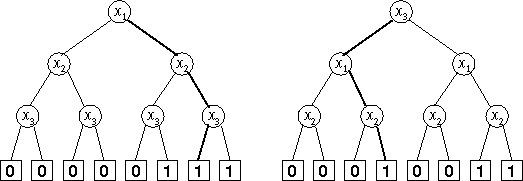
Figure 1: S-trees for the x1 and (x2 or x3) function
On the picture, two S-trees representing the same Boolean function,f(x1,x2,x3)=x1 and (x2 or x3), are shown. For the left tree, the variable ordering is x1,x2,x3, and for the right tree it is x3,x1,x2.
The values of the variables x1,x2,…,xn, are given as a Variable Values Assignment (VVA)
(x1=b1,x2=b2,…,xn=bn)
with b1,b2,…,bn in {0,1}. For instance, ( x1=1,x2=1,x3=0) would be a valid VVA for n=3, resulting for the sample function above in the value f(1,1,0)=1 and (1 or 0) = 1. The corresponding paths are shown bold in the picture.
Your task is to write a program which takes an S-tree and some VVAs and computes f(x1,x2,…,xn) as described above.
Input
The input contains the description of several S-trees with associated VVAs which you have to process. Each description begins with a line containing a single integer n, 1≤n≤7, the depth of the S-tree. This is followed by a line describing the variable ordering of the S-tree. The format of that line is xi1xi2…xin. (There will be exactly n different space-separated strings). So, for n=3 and the variable ordering x3,x1,x2, this line would look as follows:
x3x1x2
In the next line the distribution of 0’s and 1’s over the terminal nodes is given. There will be exactly 2n characters (each of which can be 0 or 1), followed by the new-line character. The characters are given in the order in which they appear in the S-tree, the first character corresponds to the leftmost terminal node of the S-tree, the last one to its rightmost terminal node.
The next line contains a single integer m, the number of VVAs, followed by m lines describing them. Each of the m lines contains exactly n characters (each of which can be 0 or 1), followed by a new-line character. Regardless of the variable ordering of the S-tree, the first character always describes the value of x1, the second character describes the value of x2, and so on. So, the line
110
corresponds to the VVA ( x1=1,x2=1,x3=0).
The input is terminated by a test case starting with n=0. This test case should not be processed.
Output
For each S-tree, output the line “S-Tree #j:”, where j is the number of the S-tree. Then print a line that contains the value of f(x1,x2,…,xn) for each of the given m VVAs, where f is the function defined by the S-tree.
Output a blank line after each test case.
Samples
Input
3
x1 x2 x3
00000111
4
000
010
111
110
3
x3 x1 x2
00010011
4
000
010
111
110
0
Output
S-Tree #1:
0011
S-Tree #2:
0011
translate :
Give a full binary tree , Each layer represents a 01 Variable , take 0 Go to the left when , take 1 Go to the right when .
for example , The left and right figures above correspond to expressions x1∧(x2∨x3).
Give the values of all leaves and some queries ( That is, each variable ), Find the value of the leaf reached by each query . for example , There are four queries :000、010、111、110, Then the output should be 0011.
Explain it. :
① The above expression means x2 and x3 At least one is 1, also x1 yes 1 The value of the leaf node reached by the query is 1( This may be the idea of some advanced practice , Although I knew what he meant, I didn't expect how to realize it with conjunction and disjunction )
② Explain directly according to the example :
a. First enter a value n It means that there are several layers x.
b. Input x?,x?,x?, The order is expressed on which layer , such as x3 x1 x2 Express x3 It's the first floor ,x1 It's the second floor ,x2 It's the third floor .
c. Enter the final query leaf node 01 value ( share 2 Of n The number of power ).
d. Enter the number of queries t.
e. Enter the query method , The order represents x The subscript , such as 110, Refer to x1 towards the right ,x2 towards the right ,x3 towards the left .( Note that it is not in the order of layers )
AC Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+5;
const ll mod = 1e9+7;
int main()
{
int n,T=0;
while(cin>>n && n)
{
int qq = pow(2,n);
char c;
int x[10]={
0};// Access order records
int k[10]={
0}; // Record whether each position is left or right .
int w[1000]={
0};// Record the value at the end 0/1
int ans[10]={
0};// answer
for(int i=1;i<=n;i++)
cin>>c>>x[i];
for(int i=0;i<qq;i++)
{
cin>>c;
w[i+qq] = c-'0';
}
int t;
cin>>t;
for(int i=1;i<=t;i++)
{
for(int j=1;j<=n;j++)
{
cin>>c;
k[j] = c-'0';
}
int tmp=1;
for(int j=1;j<=n;j++)
{
if(k[x[j]]==1)
tmp = tmp*2+1;
else
tmp = tmp*2;
}
ans[i] = w[tmp];
}
cout<<"S-Tree #"<<++T<<":"<<endl;
for(int i=1;i<=t;i++)
cout<<ans[i];
cout<<endl<<endl;
}
}
Ideas :
① The root node is 1, turn left ×2, turn right ×2+1.
② Save the last node with an array 01 The number .
③ Record the order of layers .
④ Record x1,x2,x3 Of 01 Method , Then operate one by one according to the order of layers .
⑤ Got tmp Is the coordinates of the leaves Take this number from the array and save it answer ans Array
边栏推荐
- Learning record: use STM32 external input interrupt
- mysql导入数据库报错 [Err] 1273 – Unknown collation: ‘utf8mb4_0900_ai_ci’
- China chart recorder market trend report, technology dynamic innovation and market forecast
- China earth moving machinery market trend report, technical dynamic innovation and market forecast
- C语言数组的概念
- Market trend report, technical innovation and market forecast of lip care products in China and Indonesia
- Web based photo digital printing website
- 渗透测试 ( 3 ) --- Metasploit Framework ( MSF )
- Cost accounting [14]
- Opencv learning log 15 count the number of solder joints and output
猜你喜欢
Nodejs+vue online fresh flower shop sales information system express+mysql

STM32如何使用STLINK下载程序:点亮LED跑马灯(库版本)
信息安全-威胁检测-NAT日志接入威胁检测平台详细设计
Ball Dropping
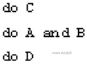
【高老师UML软件建模基础】20级云班课习题答案合集
力扣刷题记录
信息安全-安全编排自动化与响应 (SOAR) 技术解析
Learning record: understand systick system timer and write delay function
1010 things that college students majoring in it must do before graduation

Information security - Analysis of security orchestration automation and response (soar) technology
随机推荐
渗透测试 ( 1 ) --- 必备 工具、导航
Accounting regulations and professional ethics [5]
渗透测试 ( 4 ) --- Meterpreter 命令详解
Printing quality inspection and verification system Industry Research Report - market status analysis and development prospect forecast
想应聘程序员,您的简历就该这样写【精华总结】
China's earthwork tire market trend report, technical dynamic innovation and market forecast
信息安全-威胁检测-flink广播流BroadcastState双流合并应用在过滤安全日志
CEP used by Flink
Opencv learning log 30 -- histogram equalization
毕业才知道IT专业大学生毕业前必做的1010件事
入门C语言基础问答
Cost accounting [16]
mysql导入数据库报错 [Err] 1273 – Unknown collation: ‘utf8mb4_0900_ai_ci’
区间和------离散化
Cost accounting [20]
VS2019初步使用
数据在内存中的存储&载入内存,让程序运行起来
Path problem before dynamic planning
0-1背包问题(一)
Opencv learning log 12 binarization of Otsu method