当前位置:网站首页>[exercise-9] Zombie's Treasury test
[exercise-9] Zombie's Treasury test
2022-07-06 15:56:00 【Flame car】
The main idea of the topic :
Some brave soldiers came to a lost village . They are very lucky , Found many treasures and a big treasure chest , But also found angry zombies .
The soldiers are very brave , They decided to defeat the zombies , Then bring back all the treasures . A long and brutal battle continued from morning till night , The soldiers found that zombies are immortal , Invincible .
Of course , The treasure should not be left here . Unfortunately , Due to the limitation of treasure chest capacity , Soldiers can't carry all the treasures in treasure chest . in fact , There are only two kinds of treasures : Emeralds and Sapphires . All emeralds are equal in size and value , And the number is infinite . Sapphire, too .
As a priest of soldiers with magical artifacts : The computer , Considering the size of the box , The value and size of each gem , You should calculate the maximum value of the treasure that our soldiers can bring back .
AC Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+5;
const ll mod = 1e9+7;
struct node{
ll s,v;
};
node mx,mn,a[2];
int main()
{
int t,V;
cin>>t;
for(int i=1;i<=t;i++)
{
cin>>V>>a[0].s>>a[0].v>>a[1].s>>a[1].v;
ll t1 = a[0].v*a[1].s;
ll t2 = a[1].v*a[0].s;
ll res = 0;
if(t1>=t2)
mx.s=a[0].s,mx.v=a[0].v,mn.s=a[1].s,mn.v=a[1].v;
else
mx.s=a[1].s,mx.v=a[1].v,mn.s=a[0].s,mn.v=a[0].v;
ll top = V/mn.s;
top = min(top,mx.s-1);
for(ll j=0;j<=top;j++)
{
ll tmp1=j*mn.v;
ll tmp2=(V-j*mn.s)/mx.s*mx.v;
res = max(res,tmp1+tmp2);
}
printf("Case #%d: %lld\n",i,res);
}
return 0;
}
What this problem simplifies is to take the range of the number of low value items .
First , We know :
The volume of the box is V
Every item 1 The volume of is s1, The value is v1.
Every item 2 The volume of is s2 , The value is v2.
Then there should be s2 Items 1 when , goods 1 The volume of is s2 * s1, The value is s2 * v1.
Similarly, there should be s1 Items 2 when , goods 2 The volume of is s1 * s2, The value is s1 * v2.
Obviously at this time : goods 1 Volume = goods 2 Volume , and goods 1 The value of Not necessarily equal to goods 2 The value of .
Let's assume that the objects in the same volume 1 Higher value :
That is to say, the volume is the same ,s2 * v1 > s1 * v2.
On the other hand , When there is s1 Items 2 His value must be lower than s2 Items 1, So the object 2 The quantity of must be less than s1 Of .
in other words , goods 1 Take as much as possible , And objects 2 Most take s1-1 individual .
Of course, this is not the simplest , Obviously take the least common multiple lcm Time items 2 Get fewer ( Less time complexity ).
边栏推荐
- C语言是低级和高级的分水岭
- Find 3-friendly Integers
- CEP used by Flink
- Record of brushing questions with force deduction -- complete knapsack problem (I)
- Research Report on surgical fluid treatment industry - market status analysis and development prospect prediction
- 【练习-1】(Uva 673) Parentheses Balance/平衡的括号 (栈stack)
- Learning record: use stm32f1 watchdog
- Cost accounting [23]
- Cost accounting [15]
- 动态规划前路径问题
猜你喜欢

C语言是低级和高级的分水岭
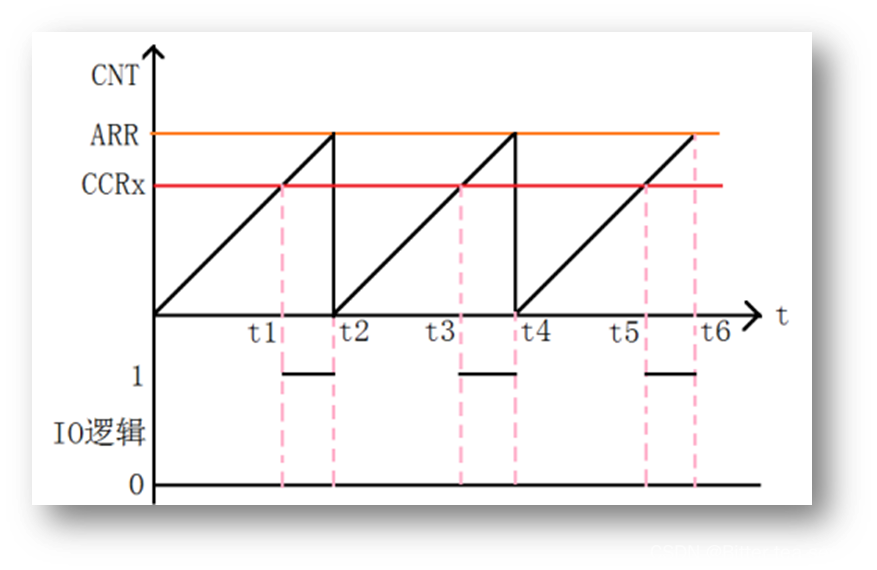
Learning record: how to perform PWM output
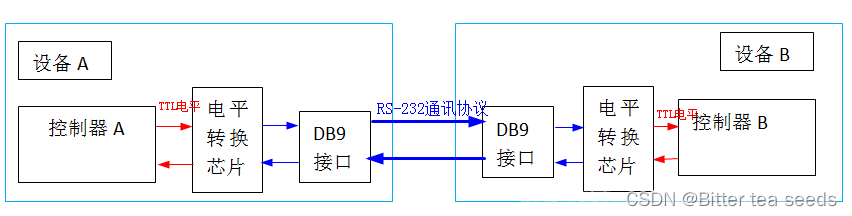
Learning record: USART serial communication

【练习-4】(Uva 11988)Broken Keyboard(破损的键盘) ==(链表)
VS2019初步使用
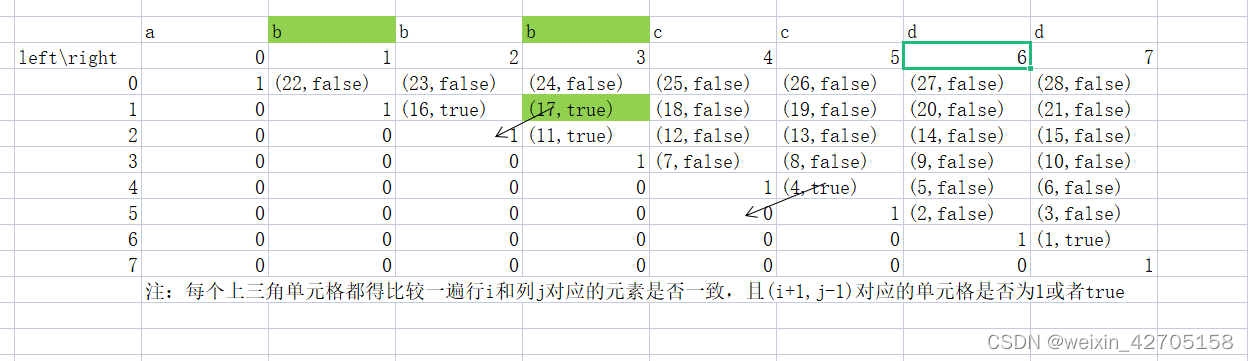
力扣刷题记录
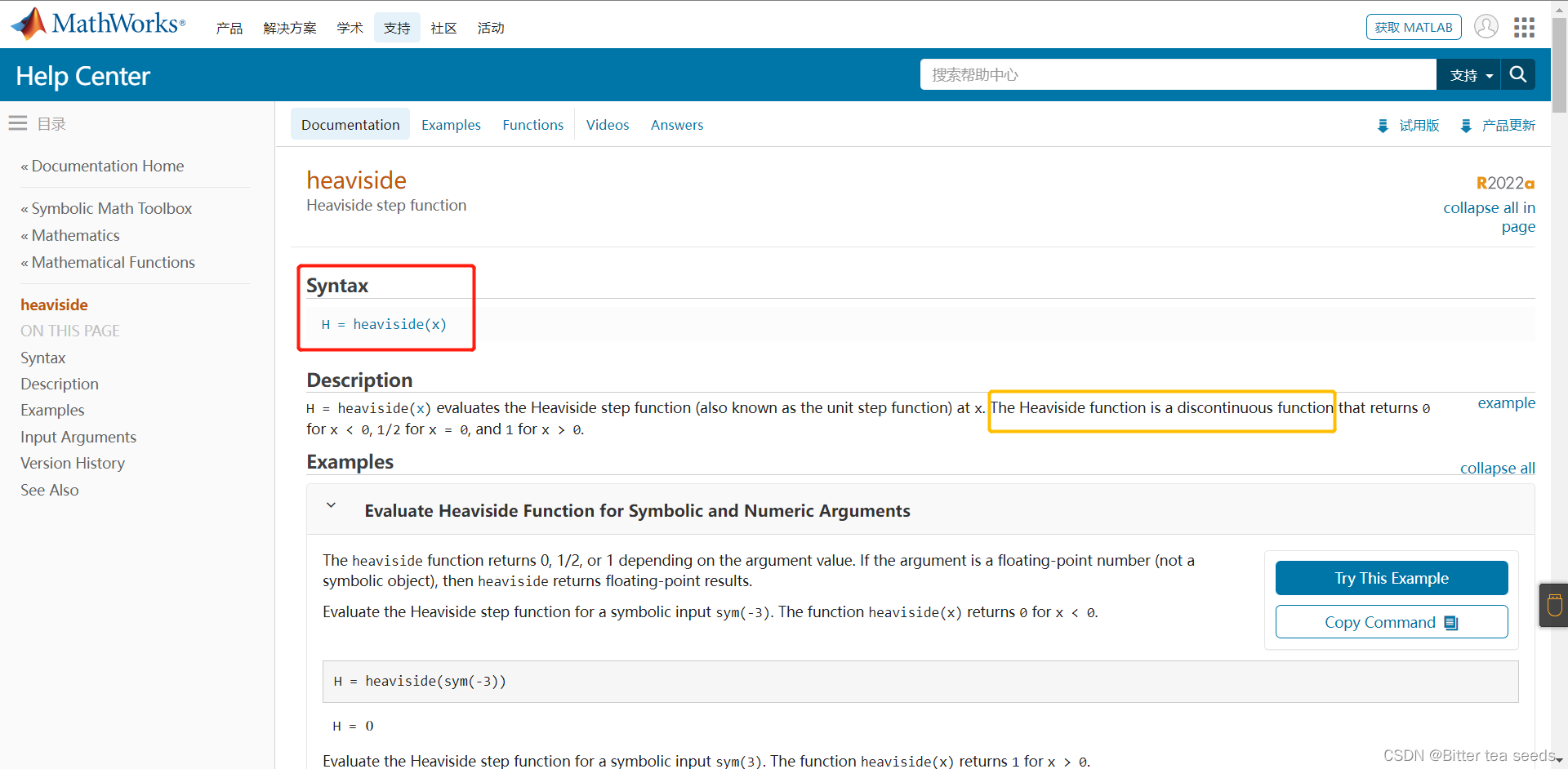
Matlab example: two expressions of step function
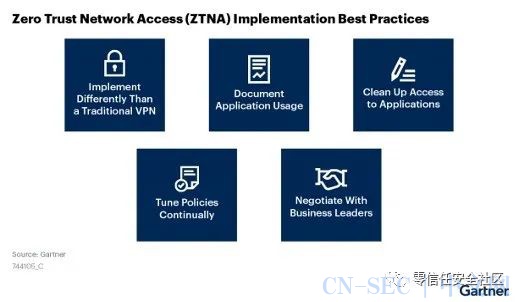
Gartner:关于零信任网络访问最佳实践的五个建议
1010 things that college students majoring in it must do before graduation
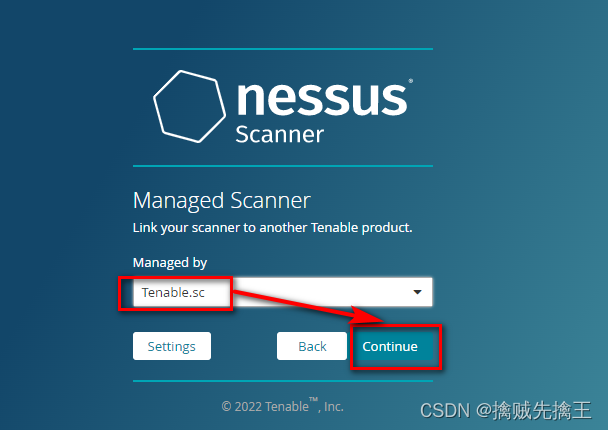
Penetration test (7) -- vulnerability scanning tool Nessus
随机推荐
Cost accounting [15]
Opencv learning log 33 Gaussian mean filtering
入门C语言基础问答
Report on the market trend, technological innovation and market forecast of printing and decorative paper in China
Research Report of exterior wall insulation system (ewis) industry - market status analysis and development prospect prediction
Learning record: Tim - Basic timer
Research Report on market supply and demand and strategy of Chinese graphic screen printing equipment industry
Learning record: understand systick system timer and write delay function
0 - 1 problème de sac à dos (1)
Opencv learning log 19 skin grinding
程序员的你,有哪些炫技的代码写法?
Accounting regulations and professional ethics [4]
The most complete programming language online API document
SSM框架常用配置文件
Research Report on market supply and demand and strategy of geosynthetics industry in China
【练习4-1】Cake Distribution(分配蛋糕)
Cost accounting [19]
mysql导入数据库报错 [Err] 1273 – Unknown collation: ‘utf8mb4_0900_ai_ci’
C语言数组的概念
【练习-6】(PTA)分而治之