当前位置:网站首页>牛顿迭代法(解非线性方程)
牛顿迭代法(解非线性方程)
2022-07-05 08:46:00 【行止AC】
原理
对于已知的方程f(x),当f’(x)=n,化为f(x)-n=0;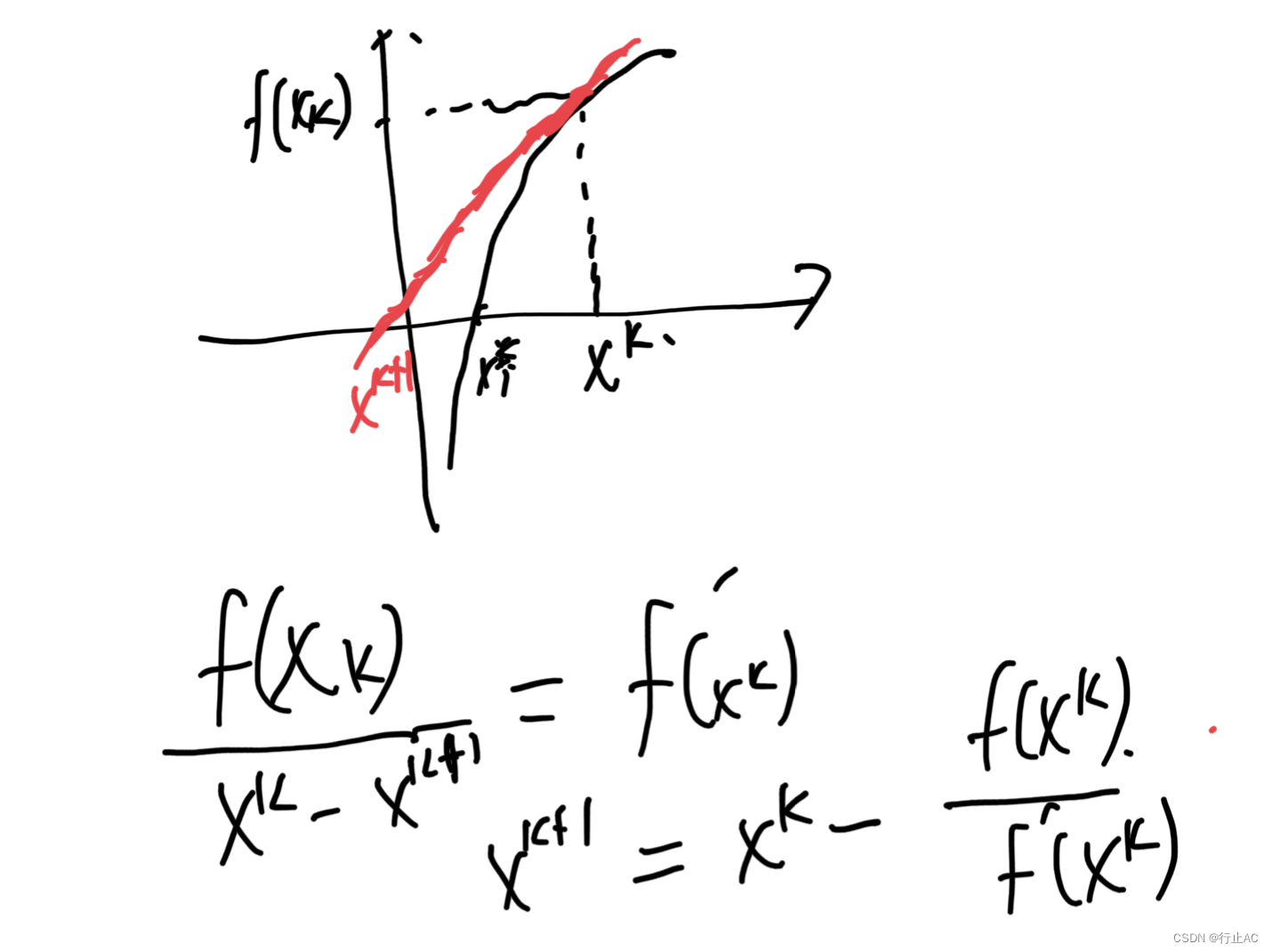
题目
#include<bits/stdc++.h>
#define ll long long
#define PI 3.141592653589793
#define E 2.718281828459045
#define HalF (l + r)>>1
#define lsn rt<<1
#define rsn rt<<1|1
#define Lson lsn, l, mid
#define Rson rsn, mid+1, r
#define QL Lson, ql, qr
#define QR Rson, ql, qr
#define myself rt, l, r
#define mset(a,b) memset(a,b,sizeof(a))
#define mcpy(a,b) memset(a,b,sizeof(a))
#define FOR( i , a , b ) for ( int i = a ; i <= b ; ++ i )
#define FO( i , n ) for ( int i = 0 ; i < n ; ++ i )
#define lowbit(a) ((a)&-(a))
#define PII pair<ll ,ll >
#define ft first
#define sd second
#define endl "\n"
typedef unsigned long long ull;
const ll mod=10007;
const ll INF=0x3f3f3f3f3f3f3f3f;
const ll Max=1e5+10;
using namespace std;
ll t,n,m,l,k;
ll ans;
/*queue<ll> q; stack<ll> s; //升序队列 priority_queue <int,vector<int>,greater<int> > q; //降序队列 priority_queue <int,vector<int>,less<int> >q;*/
double solve(double w)
{
double w1=w;
for(ll i=1;i<=100;i++)
{
w1=w1-(w1*w1*w1-w)/(3*w1*w1);
}
return w1;
}
int main()
{
ios::sync_with_stdio(false);
double n;
cin>>n;
cout<<fixed<< setprecision(6)<<solve(n)<<endl;
return 0;
}
边栏推荐
猜你喜欢
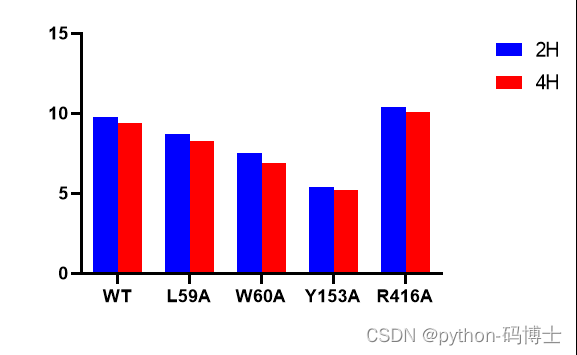
深度学习模型与湿实验的结合,有望用于代谢通量分析

Classification of plastic surgery: short in long long long
容易混淆的基本概念 成员变量 局部变量 全局变量
Use and programming method of ros-8 parameters

猜谜语啦(142)

Guess riddles (8)
Numpy pit: after the addition of dimension (n, 1) and dimension (n,) array, the dimension becomes (n, n)

Halcon blob analysis (ball.hdev)

猜谜语啦(6)

Guess riddles (2)
随机推荐
Business modeling of software model | vision
Run菜单解析
Halcon color recognition_ fuses. hdev:classify fuses by color
Solutions of ordinary differential equations (2) examples
Halcon shape_ trans
Search data in geo database
Illustration of eight classic pointer written test questions
使用arm Neon操作,提高内存拷贝速度
Meta标签详解
Guess riddles (10)
Oracle advanced (III) detailed explanation of data dictionary
It cold knowledge (updating ing~)
Xrosstools tool installation for X-Series
Guess riddles (2)
IT冷知识(更新ing~)
Meta tag details
Multiple linear regression (sklearn method)
皮尔森相关系数
golang 基础 ——map、数组、切片 存放不同类型的数据
kubeadm系列-01-preflight究竟有多少check
