当前位置:网站首页>P3250 [HNOI2016] 网络 + [NECPC2022] F.Tree Path 树剖+线段树维护堆
P3250 [HNOI2016] 网络 + [NECPC2022] F.Tree Path 树剖+线段树维护堆
2022-07-03 10:21:00 【HeartFireY】
两道题思路非常像,因此集中记录一下思路和做法
P3250 [HNOI2016] 网络
题目分析
给定一棵有 n n n个节点的树, 有 m m m次如下操作:
0 a b c 表示在 ( a , b ) (a, b) (a,b)的最短路径上增加一条重要度为 c c c的边.
1 t 表示删除第 t t t次操作所增加的边
2 x 表示节点 x x x出现故障. 此时需要回答, 所有不经过 x x x节点的边中最大的重要度.
首先将边权点权化,也就是树上问题序列化,然后利用用线段树维护待查点的补集。由于线段树节点维护序列最大值,因此将节点开成大根堆,然后每个节点记录不经过该节点的路径中的最大权,以及删除的权值。
对于每个增边操作,树剖LCA求出路径所占的全部区间,然后对其补集进行修改。补集可以先对树剖求出的区间排序,然后按顺序找间隔即可。
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e5 + 10;
struct edge {
int u, v, w; } edges[N << 1];
vector<int> g[N];
int pfa[N], dep[N], siz[N], son[N], top[N], dfn[N], rnk[N], ind;
int n, m;
void dfs1(int u, int fa){
pfa[u] = fa, dep[u] = dep[fa] + 1, siz[u] = 1;
for(auto &v : g[u]){
if(v == fa) continue;
dfs1(v, u);
siz[u] += siz[v];
if(siz[v] > siz[son[u]]) son[u] = v;
}
}
void dfs2(int u, int tp){
dfn[u] = ++ind, rnk[tp] = 0, top[u] = tp;
if(!son[u]) return;
dfs2(son[u], tp);
for(auto & v: g[u]){
if(v == pfa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
namespace SegmentTree{
struct node{
priority_queue<int> val, del;
int top(){
while(val.size() && del.size() && val.top() == del.top()) val.pop(), del.pop();
return val.empty() ? -1 : val.top();
}
}tree[N << 2];
#define ls rt << 1
#define rs rt << 1 | 1
#define lson ls, l , mid
#define rson rs, mid + 1, r
void update(int rt, int l, int r, int L, int R, int val){
if(l >= L && r <= R){
val > 0 ? tree[rt].val.emplace(val) : tree[rt].del.emplace(-val);
return ;
}
int mid = l + r >> 1;
if(mid >= L) update(lson, L, R, val);
if(mid < R) update(rson, L, R, val);
}
int query(int rt, int l, int r, int pos){
if(l == r) return tree[rt].top();
int mid = l + r >> 1, ans = tree[rt].top();
if(mid >= pos) ans = max(ans, query(lson, pos));
else ans = max(ans, query(rson, pos));
return ans;
}
}
#define pii pair<int,int>
#define fir first
#define sec second
void update(int u, int v, int w){
vector<pii> interval;
while(top[u] != top[v]){
if(dep[top[u]] < dep[top[v]]) swap(u, v);
interval.emplace_back(make_pair(dfn[top[u]], dfn[u]));
u = pfa[top[u]];
}
interval.emplace_back(make_pair(min(dfn[u], dfn[v]), max(dfn[u], dfn[v])));
sort(interval.begin(), interval.end());
int modl = 1;
for(auto & [l, r] : interval){
int modr = l - 1;
if(modl <= l - 1) SegmentTree::update(1, 1, n, modl, modr, w);
modl = r + 1;
}
if(modl <= n) SegmentTree::update(1, 1, n, modl, n, w);
}
inline void solve(){
cin >> n >> m;
for(int i = 1; i <= n - 1; i++){
int u, v; cin >> u >> v;
g[u].emplace_back(v);
g[v].emplace_back(u);
}
dfs1(1, 0);
dfs2(1, 1);
for(int i = 1; i <= m; i++){
int op; cin >> op;
if(op == 0){
cin >> edges[i].u >> edges[i].v >> edges[i].w;
update(edges[i].u, edges[i].v, edges[i].w);
}
else if(op == 1){
int t; cin >> t;
auto &[u ,v, w] = edges[t];
update(u, v, -w);
}
else{
int x; cin >> x;
cout << SegmentTree::query(1, 1, n, dfn[x]) << endl;
}
}
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
solve();
return 0;
}
[NECPC2022] F.Tree Path
给定一棵树,包含 n n n个节点和 k k k条带权路径,要求支持操作:
- 删除最小的带权路径
- 对于给定的节点 x x x,输出所有不经过 x x x的带权路径中的最小值
跟上道题思路类似,用线段树维护待查节点的补集,注意这里求得是最小值。
注意必须离散化,否则 m a p map map上多个 l o g log log炸常数过不去。
#include <bits/stdc++.h>
#pragma gcc optimize('O2')
//#define int long long
#define endl '\n'
using namespace std;
const int N = 1e5 + 10, INF = 0x3f3f3f3f;
struct edge {
int u, v, w; const bool operator< (const edge &x) {
return w < x.w; }} edges[N];
vector<int> g[N];
int n, k, m;
int pfa[N], dep[N], siz[N], son[N], top[N], dfn[N], rnk[N], ind;
bool del[N];
void dfs1(int u, int fa){
pfa[u] = fa, dep[u] = dep[fa] + 1, siz[u] = 1;
for(auto &v : g[u]){
if(v == fa) continue;
dfs1(v, u);
siz[u] += siz[v];
if(siz[v] > siz[son[u]]) son[u] = v;
}
}
void dfs2(int u, int tp){
dfn[u] = ++ind, rnk[tp] = 0, top[u] = tp;
if(!son[u]) return;
dfs2(son[u], tp);
for(auto & v: g[u]){
if(v == pfa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
namespace SegmentTree{
struct node{
priority_queue<int, vector<int>, greater<>> val;
int top(){
while(val.size() && del[val.top()]) val.pop();
return val.empty() ? INF : val.top();
}
}tree[N << 2];
#define lson rt << 1, l, mid
#define rson rt << 1 | 1, mid + 1, r
void update(int rt, int l, int r, int L, int R, int val){
if(l >= L && r <= R){
tree[rt].val.emplace(val);
return;
}
int mid = l + r >> 1;
if(mid >= L) update(lson, L, R, val);
if(mid < R) update(rson, L, R, val);
}
int query(int rt, int l, int r, int pos){
if(l == r) return tree[rt].top();
int mid = l + r >> 1, ans = tree[rt].top();
if(mid >= pos) ans = min(ans, query(lson, pos));
else ans = min(ans, query(rson, pos));
return ans;
}
}
#define pii pair<int,int>
#define fir first
#define sec second
void update(int u, int v, int w){
vector<pii> interval;
while(top[u] != top[v]){
if(dep[top[u]] < dep[top[v]]) swap(u, v);
interval.emplace_back(make_pair(dfn[top[u]], dfn[u]));
u = pfa[top[u]];
}
interval.emplace_back(make_pair(min(dfn[u], dfn[v]), max(dfn[u], dfn[v])));
sort(interval.begin(), interval.end());
int modl = 1;
for(auto & [l, r] : interval){
int modr = l - 1;
if(modl <= l - 1) SegmentTree::update(1, 1, n, modl, modr, w);
modl = r + 1;
}
if(modl <= n) SegmentTree::update(1, 1, n, modl, n, w);
}
vector<int> v(1, -0x3f3f3f3f);
inline void solve(){
cin >> n >> k >> m;
auto get = [&](int x) {
return lower_bound(v.begin(), v.end(), x) - v.begin(); };
auto dis = [&]() {
sort(v.begin(), v.end()); v.erase(unique(v.begin(), v.end()), v.end()); };
for(int i = 1; i <= n - 1; i++){
int u, v; cin >> u >> v;
g[u].emplace_back(v);
g[v].emplace_back(u);
}
dfs1(1, 0), dfs2(1, 1);
for(int i = 1; i <= k; i++){
cin >> edges[i].u >> edges[i].v >> edges[i].w;
v.emplace_back(edges[i].w);
}
dis();
for(int i = 1; i <= k; i++){
auto &[u, v, w] = edges[i];
update(u ,v, get(w));
}
int min_pos = 1, last = 0;
for(int i = 1; i <= m; i++){
int op = 0; cin >> op;
if(op == 1){
int x; cin >> x, x = x ^ last;
int ans = SegmentTree::query(1, 1, n, dfn[x]);
last = (ans == INF ? -1 : v[ans]);
cout << last << endl;
}
else{
//auto &[u, v, w] = edges[min_pos++];
del[min_pos++] = 1;
}
}
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
solve();
return 0;
}
边栏推荐
- 触摸与屏幕自动旋转调试
- 用了这么久线程池,你真的知道如何合理配置线程数吗?
- 表空间创建管理及控制文件管理
- 活动预告 | 直播行业“内卷”,以产品力拉动新的数据增长点
- Application of high-precision indoor positioning technology in safety management of smart factory
- Google Earth Engine(GEE)——GHSL 全球人口网格数据集250米分辨率
- 如何成为一名高级数字 IC 设计工程师(1-2)Verilog 编码语法篇:Verilog 1995、2001、2005 标准
- Kotlin's use of the no Arg compiler plug-in in gradle
- ConstraintLayout跟RelativeLayout嵌套出现的莫名奇妙的问题
- AMS Series 1 - AMS startup process
猜你喜欢

行业唯一!法大大电子合同上榜36氪硬核科技企业
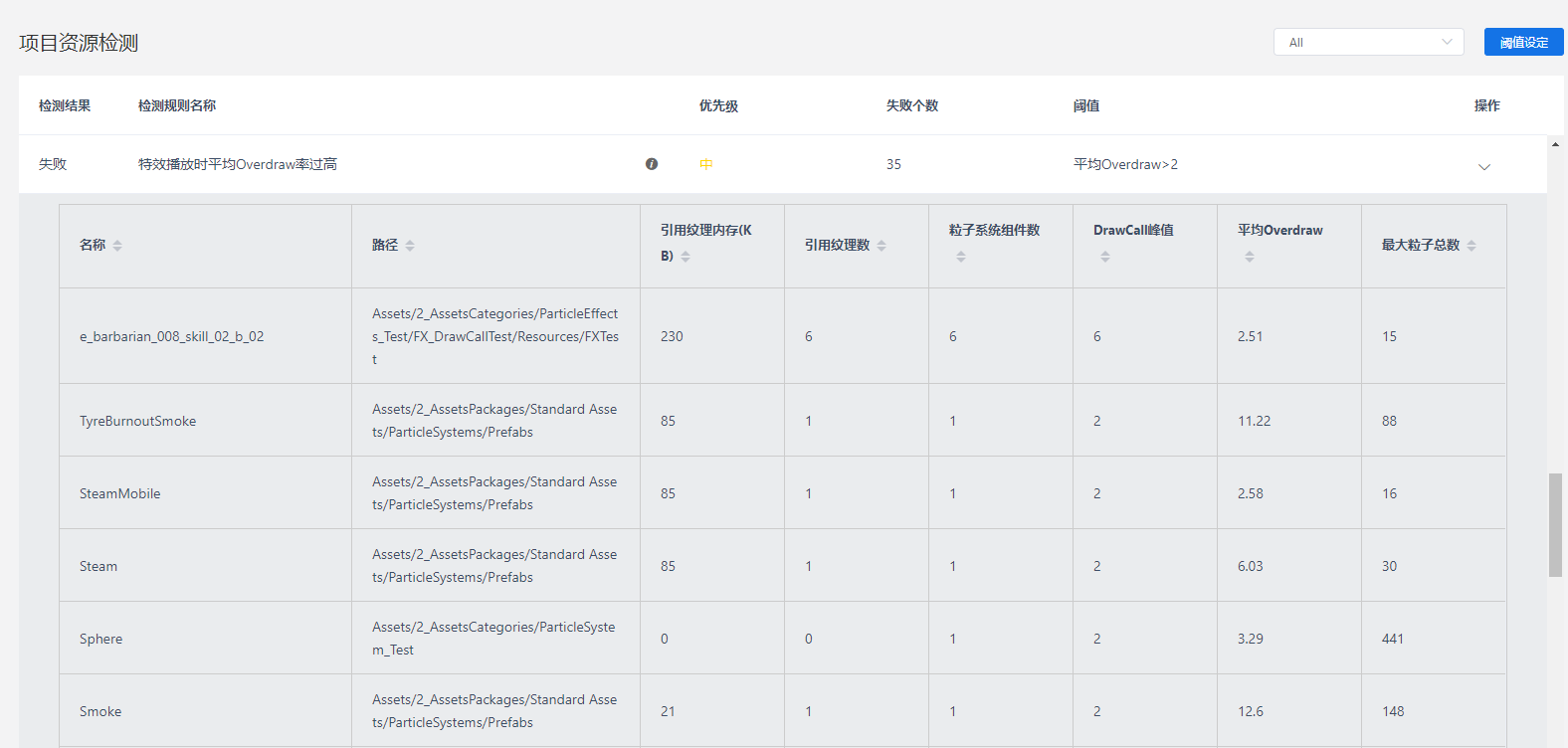
Balance between picture performance of unity mobile game performance optimization spectrum and GPU pressure

【obs】obs的ini格式的ConfigFile
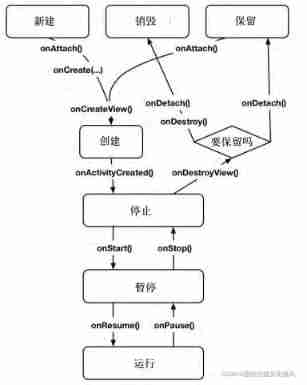
Activity and fragment lifecycle

How did I grow up in the past eight years as a test engineer of meituan? I hope technicians can gain something after reading it

Expandablelistview that can expand and shrink (imitating the list page of professional selection of Zhilian recruitment)
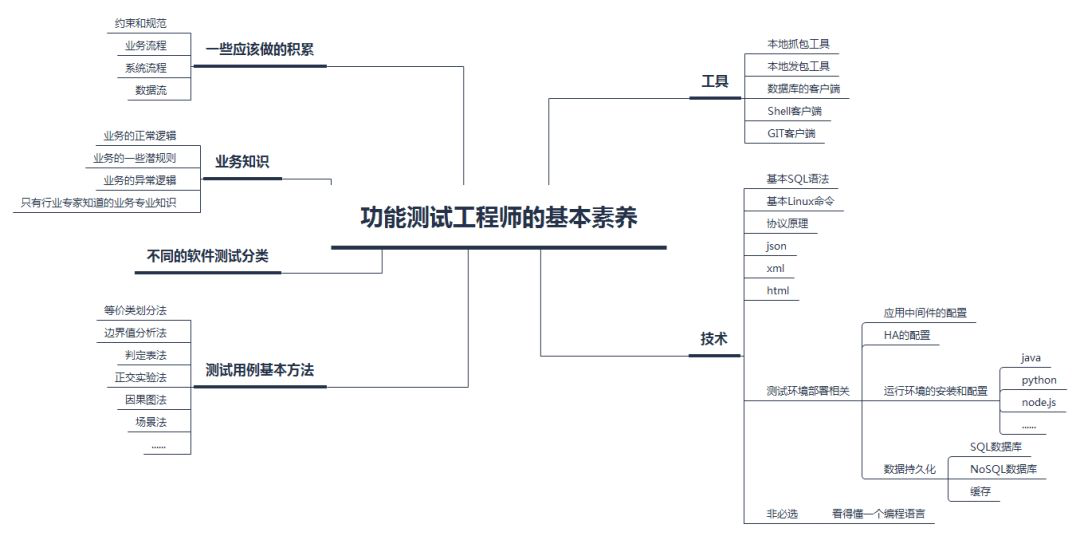
I have been doing software testing for three years, and my salary is less than 20K. Today, I put forward my resignation

高精度室内定位技术,在智慧工厂安全管理的应用
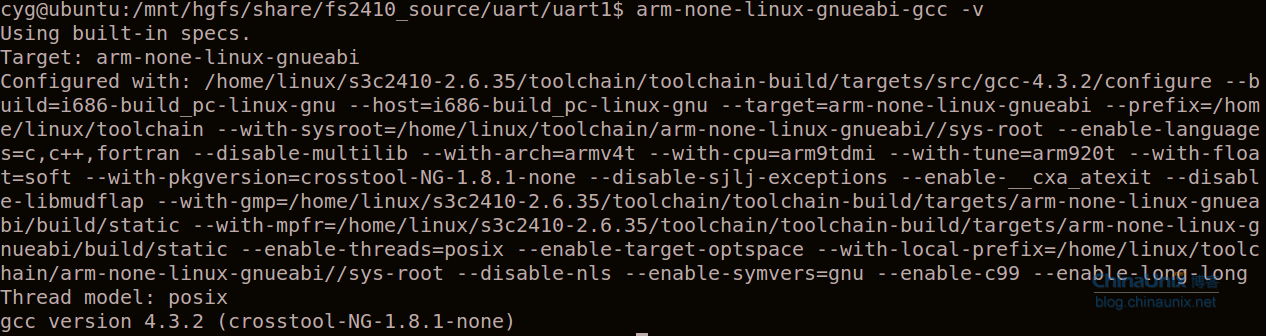
解决undefined reference to `__aeabi_uidivmod‘和undefined reference to `__aeabi_uidiv‘错误

MATLAB提取不规则txt文件中的数值数据(简单且实用)
随机推荐
触摸与屏幕自动旋转调试
在腾讯云容器服务Node上执行 kubectl
【obs】obs的ini格式的ConfigFile
Activity and fragment lifecycle
Cuiyusong, CTO of youzan: the core goal of Jarvis is to make products smarter and more reliable
Driver development based on I2C protocol
Technical experts from large factories: how can engineers improve their communication skills?
glassfish org. h2.server. Shutdownhandler classnotfoundexception exception exception handling
Ext file system mechanism principle
After a month, I finally got Kingdee offer! Share tetrahedral Sutra + review materials
程序进程管理工具-go supervisor
Touch and screen automatic rotation debugging
Encapsulation attempt of network request framework of retro + kotlin + MVVM
One hot code
C语言 AES加解密
Internet Socket (非)阻塞write/read n个字节
【obs】封装obs实现采集的基础流程
Definition and properties of summation symbols
如何成为一名高级数字 IC 设计工程师(1-5)Verilog 编码语法篇:操作数
asyncio 警告 DeprecationWarning: There is no current event loop