[200 opencv routines] 223 Polygon fitting for feature extraction (cv.approxpolydp)

『youcans Of OpenCV routine 200 piece - General catalogue 』

【youcans Of OpenCV routine 200 piece 】223. Polygon fitting for feature extraction

Basic concept of target characteristics

Multiple regions are obtained by image segmentation , Get the pixel set in the region or the pixel set at the boundary of the region . We call people or things we are interested in as goals , The area where the target is located is the target area .
The feature is usually aimed at a certain target in the image . After image segmentation , The target area should also be properly represented and described , For the next step .
“ Express ” It is to express the goal directly and concretely , To save storage space 、 Convenient feature calculation . Representation of goals , Chain code 、 Polygonal approximation （MPP）、 Slope marking diagram 、 Boundary segmentation 、 Area skeleton .
“ describe ” It is an abstract expression of the goal , On the basis of distinguishing different goals , Try to measure the target 、 translation 、 Rotation change insensitive .

Boundary feature descriptor

The boundary descriptor of the target （Boundary descriptors）, Also called boundary descriptor .
The outline is the description of the target boundary , The contour attribute is the basic boundary descriptor .

for example ：

• The length of the boundary , The number of pixels of the contour is an approximate estimate of the perimeter of the boundary ;
• The diameter of the boundary , The length of the long axis of the boundary , Equal to the length of the long side of the rectangular bounding box with the smallest contour ;
• Eccentricity of boundary , The ratio of the major axis to the minor axis of the boundary , Equal to the length width ratio of the smallest rectangular bounding box of the contour ;
• The curvature of the boundary , Slope difference of adjacent boundary segments ;
• Chain code , The boundary is represented by a straight line segment with a specified length and direction ;
• Fourier descriptor , Fourier coefficients obtained by discrete Fourier transform of two-dimensional boundary points , For rotation 、 translation 、 Scale and start point are insensitive ;
• Statistical moments , Treat the boundary as a histogram function , Describe the boundary features with image moments , With translation 、 Grayscale 、 scale 、 Rotation invariance .

### routine 12.12： Polygon fitting of contour

OpenCV The function in cv.approxPolyDP() It can be used for polygon fitting of image contour points .

Function description ：

	cv.approxPolyDP(curve, epsilon, closed[, approxCurve=None]) → approxCurve

function cv.approxPolyDP Use Douglas-Peucker The algorithm finds a polyline with fewer vertices / polygon , Approximate the input curve or polygon with the specified accuracy .（ Reference resources ： Fit a straight line , Fit ellipse ）

Parameter description ：

• curve： Input point set , Set of two-dimensional point vectors
• approxCurve： Output point set , Represents a fitting curve or polygon , Data and input parameters curve Agreement
• epsilon： Specified approximate accuracy , The maximum distance between the original curve and the approximate curve
• close： Closing sign ,True Represents a closed polygon ,False Indicates that the polygon is not closed

matters needing attention ：

Douglas-Peucker Algorithm ：
（1） At the beginning of the curve A And the end B Make a straight line between AB, Is the chord of the curve ;
（2） Find the point on the curve with the largest distance from the straight line C, Calculate its relation with AB Distance of d;
（3） Comparison distance d And the set threshold threshold, If it is less than the set threshold, the straight line segment is used as the approximation of the curve , The curve processing is completed .
（4） If distance d Greater than the set threshold , with C Point will curve AB It's divided into two parts AC and BC, And carry out the above steps for these two paragraphs .
（5） When all curves are processed , Connect the broken line formed by all the dividing points in turn , As an approximation of the curve .

    # 12.12  Polygon fitting of contour 
    img = cv2.imread("../images/Fig1105.tif", flags=1)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  #  Grayscale image 
    blur = cv2.boxFilter(gray, -1, (5, 5))  #  Box filter ,9*9  Smooth nucleus 
    _, binary = cv2.threshold(blur, 205, 255, cv2.THRESH_OTSU + cv2.THRESH_BINARY)

    #  Find the outline in the binary graph 
    contours, hierarchy = cv2.findContours(binary, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)  # OpenCV4~
    print('len:', len(contours))
    #  Draw all contours ,contourIdx=-1  Draw all contours 
    imgCnts = np.zeros(gray.shape[:2], np.uint8)  #  The draw contour function will modify the original image 
    imgCnts = cv2.drawContours(imgCnts, contours, -1, (255, 255, 255), thickness=2)  #  Draw all contours 

    plt.figure(figsize=(9, 6))
    plt.subplot(231), plt.axis('off'), plt.title("Origin")
    plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
    plt.subplot(232), plt.axis('off'), plt.title("Binary")
    plt.imshow(binary, 'gray')
    plt.subplot(233), plt.axis('off'), plt.title("Contour")
    plt.imshow(imgCnts, 'gray')

    cnts = sorted(contours, key=cv2.contourArea, reverse=True)  #  All profiles are sorted by area 
    cnt = cnts[0]  #  The first  0  A profile , The outline with the largest area ,(664, 1, 2)
    print("shape of max contour:", cnt.shape[0])

    eps = [50, 30, 10]
    for i in range(len(eps)):
        polyFit = cv2.approxPolyDP(cnt, eps[i], True)
        print("eps={}, shape of fitting polygon:{}".format(eps[i], polyFit.shape[0]))
        fitContour = np.zeros(gray.shape[:2], np.uint8)  #  Initialize the maximum contour image 
        cv2.polylines(fitContour, [cnt], True, 205, thickness=2)  #  Draw the maximum outline , Polygonal curve 
        cv2.polylines(fitContour, [polyFit], True, 255, 3)
        plt.subplot(2,3,i+4), plt.axis('off'), plt.title("approxPoly(eps={})".format(eps[i]))
        plt.imshow(fitContour, 'gray')

    plt.tight_layout()
    plt.show()

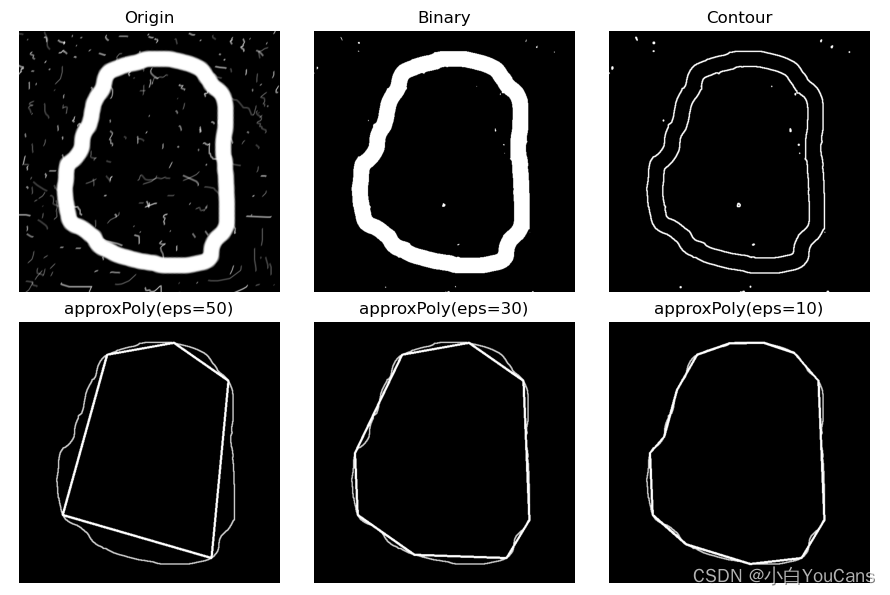
Running results ：
shape of max contour: 547
eps=50, shape of fitting polygon:5
eps=30, shape of fitting polygon:8
eps=10, shape of fitting polygon:13

The results show that , use 13 A polygon with vertices can well approach the boundary of the contour , Describe the boundary features of the contour , Significantly reduce the amount of data .

【 At the end of this section 】

Copyright notice ：
[email protected] Original works , Reprint must be marked with the original link ：(https://blog.csdn.net/youcans/article/details/125598167)
Copyright 2022 youcans, XUPT
Crated：2022-6-30

197. The basic features of the contour
200. Basic properties of the contour
223. Polygon fitting for feature extraction