Blue Bridge Cup 2022 13th provincial competition real topic - block painting

Write it at the front

I went online to search the solutions of other bloggers , Because I really can't understand d p [ i ] = d p [ i − 1 ] ⋅ 2 + d p [ i − 3 ] dp[i] = dp[i-1]\cdot2+dp[i-3] dp[i]=dp[i−1]⋅2+dp[i−3] How is this state transition equation obtained （ Maybe I'm too stupid ）, Most of their explanations are cursory, and the ending is a little vague , As a vegetable dog, I'm really hard to understand ！ After thinking for a long time, I came up with my own idea of solving this problem , It is different from the mainstream state transition equation on the Internet, but it can also solve problems .

Blue Bridge Cup 2022 True title of the 13th provincial competition in - Building block painting

The time limit : 1Sec Memory limit : 256MB Submit : 623 solve : 135

Title Description

Xiao Ming has recently become addicted to building block painting , There are two types of building blocks , Respectively I type （ The size is 2 Unit area ） and L type （ The size is 3 Unit area ）：

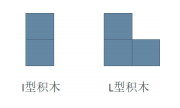
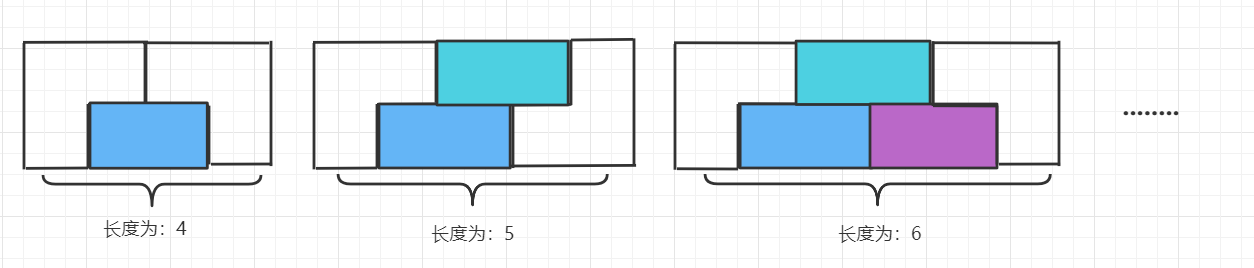
meanwhile , Xiao Ming has an area of 2 × N Canvas of , Canvas by 2 × N individual 1 × 1 Regional composition . Xiao Ming needs to fill the canvas with the above two kinds of building blocks , He wanted to know how many different ways there were ？ The building blocks can rotate freely , And the direction of the canvas is fixed .

Input

Enter an integer N, Represents the canvas size .

Output

Output an integer for the answer . Because the answer can be big , So output it to 1000000007 The value after taking the mold .

Sample input copy

3

Sample output copy

5

Tips

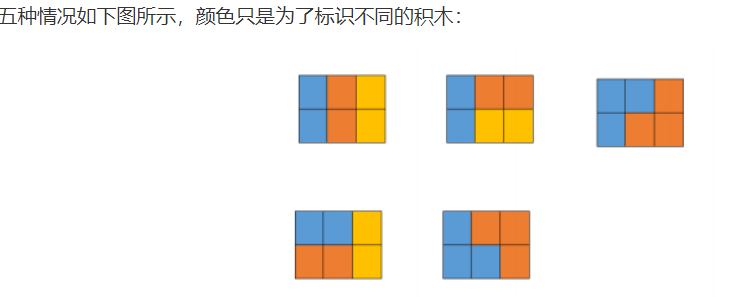
The five cases are shown in the figure below , The color is just to identify different building blocks ：

For all test cases ,1 ≤ N ≤ 10000000.

Their thinking 1️⃣:

Ah , However, when it is a game, it is impossible to measure another data , What a pity , But the idea is right when writing , unfortunately a[2][1] Write the wrong .

Ideas ：a[i][0]:i The stacking method of building blocks ,a[i][1]：i The stacking method of adding a small square .

Such as ：

perhaps

No matter how these three pieces are put , All call a[3][0].
If there is a small square on the right on this basis, it is called a[3][1], Note that the small square can be one row above the fourth column or one row below the fourth column （ If it's hard to find the picture, I won't give it , Imagine for yourself ）

The dynamic programming equation is given ：

 a[i][0]=(a[i-2][0]+a[i-2][1]+a[i-1][0])%mod; 
a[i][1]=(a[i-1][0]*2+a[i-1][1])%mod;

Canvas size is i The arrangement of , Both a[i][0] Value ：

1. Consider one less piece first I The arrangement of type a building blocks , Both a[i-1][0], Then add a piece I Type block is OK ,
2. Consider one less piece L The arrangement of type a building blocks , Both a[i-2][1], Then add a piece L Type block is OK ,
3. Consider two less I The arrangement of type a building blocks , Both a[i-2][0], Add two I Type building blocks , Be careful , Two pieces must be added horizontally , If it's vertical , It is equivalent to the first type of arrangement , repeated .
4. When it comes to missing more building blocks , You will find that no matter how you line up , The arrangement will repeat the above , in other words , The above three cases cover a[i][0] All the arrangements of .

So there is ：

a[i][0]=(a[i-2][0]+a[i-2][1]+a[i-1][0])%mod;

a[i][1] The arrangement of , You can draw and write by yourself .

Write the initial state ：

a[1][0]=1,a[2][0]=2,a[1][1]=2,a[2][1]=4;

Give the complete code ：

#include<stdio.h>
#define mod 1000000007
long int a[10000001][2];
int main()
{
    
     int n;
    a[1][0]=1,a[2][0]=2,a[1][1]=2,a[2][1]=4;
    scanf("%d",&n);
    if(n==1)printf("1");
    else if(n==2)printf("2");
    else {
    
        for(int i=3;i<=n;i++){
    
            a[i][0]=(a[i-2][0]+a[i-2][1]+a[i-1][0])%mod;
            a[i][1]=(a[i-1][0]*2+a[i-1][1])%mod;
        }
        printf("%ld",a[n][0]%mod);
    }
    return 0;
}

Disintegration thinking 2️⃣：

First of all, this problem must be done with dynamic programming , It is also in line with the idea of dynamic programming , No aftereffect is also satisfied, so we can do better with dynamic programming .
How do you think about this question , First, it is a two-dimensional matrix pattern , And there is arrangement or order , So if we want to use two dimensions dp It's really not easy to do it , Fortunately, we use one dimension to simplify the process of building blocks , But how to simplify it .
Let's first look at the case given by the topic :

First, let's look directly at the third order , The first and second we can find I There are ways to put the type-A building blocks together 2 Species , Or watch one or four , then L The splicing method of type a building blocks is 1 Look at three and five ( If you turn the two of them upside down, it's a kind of ), Then we might as well think simply, so the recursive formula is :dp[i]=dp[i-1]*2+dp[i-3];

The method of proof is the thought process we just had , We treat two-dimensional matrices as one-dimensional , therefore I Type a building block is equal to 1 A square , So we remember as i-1,L Type a building block is equal to 1.5 A square , however L Type a building block cannot appear alone , Must appear in pairs , So we remember as i-3, And because of I There are two ways for type a building blocks to appear in one position , So we multiply by two ,L The only way for a block to appear is to multiply it by 1, It's over .

But we still need to initialize the first three :

When i be equal to 1 When dp Namely 1, There's nothing to that , You can only put one I The type is the same no matter how you put it .
When i be equal to 2 When dp yes 2, Because you can put two I type , It can be placed horizontally or vertically 2 Kind of .
When i be equal to 3 It's the situation in the topic dp be equal to 5,

Reference code :

#include<stdio.h>
#include<string.h>
#define mod 1000000007
int dp[10000005];
int main()
{
    
    int n;
    scanf("%d",&n);
    memset(dp,0,sizeof(dp));
    dp[1]=1,dp[2]=2,dp[3]=5;
    for(int i=4;i<=n;i++)
    {
    
        dp[i]=(dp[i-1]*2%mod+dp[i-3]%mod)%mod;
    }
    printf("%d\n",dp[n]);
    return 0;
}

Their thinking 3️⃣：

State means

The key to solving this problem is to use dynamic programming , Define a one-dimensional array d p dp dp , d p [ i ] dp[i] dp[i] The size of the storage canvas is 2 × i 2\times i 2×i The number of filling methods of building blocks .

State initialization

It's not hard to find out ：

• When the canvas size is 2 × 1 2\times 1 2×1 when , Only one... Can be put down I Type building blocks , therefore d p [ 1 ] = 1 dp[1] =1 dp[1]=1.

• When the canvas size is 2 × 2 2\times 2 2×2 when , Only two... Can be put down I Type building blocks , But the building blocks can rotate , As shown in the figure below , therefore d p [ 2 ] = 2 dp[2] = 2 dp[2]=2

  

• When the canvas size is 2 × 3 2\times3 2×3 when , As shown in the title , There are five ways , therefore d p [ 3 ] = 5 dp[3] = 5 dp[3]=5

Situation combing

Before combing the state transition equation , Think about , There are only a few situations when the building block painting appears at the end and conforms to the meaning of the topic ？

• Situation 1 ： Use alone I Type building block splicing

  It is entirely possible to use a separate Splice in the tail of any building block painting that conforms to the meaning of the topic , Make the building blocks draw the total length + 1.

• Situation two ： Use two I Type building block splicing

  Use It can also be spliced to the tail of any building block painting that conforms to the meaning of the topic , Draw the total length of its building blocks + 2.

• Situation three ： Use two L Type building block splicing

  Use or Splice to the tail of any building block that conforms to the meaning of the topic , Draw the total length of its building blocks +3, But note that there are two kinds of L The splicing methods of type a building blocks belong to different ways , Therefore, it needs to be calculated separately ！

• Situation four ： Use two L Type building blocks and i ( 1 , 2 , 3 , . . . . n ) i(1,2,3,…n) i(1,2,3,…n) individual I Type building block splicing

  The most easily overlooked situation ！ Use I Type building blocks and Two L T-shaped building blocks can also complete splicing .

  

  Don't forget what happens after the flip ：

  

State transition equation

• Situation 1 ： Use alone I Type building block splicing , d p [ i ] + = d p [ i − 1 ] dp[i] += dp[i-1] dp[i]+=dp[i−1]

• Situation two ： Use two I Type building block splicing , d p [ i ] + = d p [ i − 2 ] dp[i]+=dp[i-2] dp[i]+=dp[i−2]

• Situation three ： Use two L Type building block splicing , d p [ i ] + = 2 ⋅ d p [ i − 3 ] dp[i]+=2\cdot dp[i-3] dp[i]+=2⋅dp[i−3]

• Situation four ： In case 4, there is only i > = 4 i>=4 i>=4 Only when , The specific discussion is as follows ：

• if i = = 4 i4 i4 , Only exist with a length of 4 The splicing of , hypothesis d p [ 0 ] = 1 dp[0]=1 dp[0]=1, in other words d p [ 4 ] + = d p [ 0 ] ⋅ 2 dp[4]+=dp[0]\cdot 2 dp[4]+=dp[0]⋅2

• if i = = 5 i5 i5, The length of existence is 4 , 5 4,5 4,5 The splicing of , namely d p [ 5 ] + = ( d p [ 0 ] + d p [ 1 ] ) ⋅ 2 dp[5] += (dp[0]+dp[1])\cdot 2 dp[5]+=(dp[0]+dp[1])⋅2

• if i = = 6 i 6 i6, Continue to deduce that there is ： d p [ 6 ] + = ( d p [ 0 ] + d p [ 1 ] + d p [ 2 ] ) ⋅ 2 dp[6]+=(dp[0]+dp[1]+dp[2])\cdot 2 dp[6]+=(dp[0]+dp[1]+dp[2])⋅2

• if i = = 7 i7 i7, Derivation has ： d p [ 7 ] + = ( d p [ 0 ] + d p [ 1 ] + d p [ 2 ] + d p [ 3 ] ) ⋅ 2 dp[7]+=(dp[0]+dp[1]+dp[2]+dp[3])\cdot 2 dp[7]+=(dp[0]+dp[1]+dp[2]+dp[3])⋅2

According to the above derivation , It's not hard to find out d p [ i ] + = ( d p [ 0 , 1 , 2 , . . . , i − 4 ] ) ⋅ 2 dp[i]+=(dp[0,1,2,…,i-4])\cdot 2 dp[i]+=(dp[0,1,2,…,i−4])⋅2, So you can define a variable s u m sum sum Storage d p [ 0 , 1 , 2 , . . i ] dp[0,1,2,…i] dp[0,1,2,…i] Value , stay i i i Update while increasing s u m sum sum Value , The initial conditions s u m = 0 sum=0 sum=0.
Return results

Final d p [ N ] dp[N] dp[N] Is the value of the title , The problem was solved in this way .

We need to pay attention to ： Only... Is used in the following code a 1 , a 2 , a 3 a1,a2,a3 a1,a2,a3 Represent the d p [ i − 1 ] , d p [ i − 2 ] , d p [ i − 3 ] dp[i-1],dp[i-2],dp[i-3] dp[i−1],dp[i−2],dp[i−3].

Code writing

#include <iostream>
#include <math.h>
#define ll long long
// #include <bits/stdc++.h>
using namespace std;
const int MOD = 1000000007;
int main() {
    
	ll n, a1, a2, a3;
	a1 = 5;
	a2 = 2;
	a3 = 1;
	cin >> n;
	ll sum = 0;
	for (ll i = 4; i <= n; ++i) {
    
		ll val = 0;
		val += a1;
		val += a2;
		val += (a3 * 2L);
		if (i >= 4) {
    
			val += sum * 2 + 2;
			sum += a3;
		}
		val %= MOD;
		a3 = a2;
		a2 = a1;
		a1 = val;
	}
	cout << a1;
	return 0;
}

At the end 🧐

If you don't understand anything , You can comment or send me a private message ,
If it works for you , Just give this konjaku a good comment .