当前位置:网站首页>雇佣收银员【差分约束】
雇佣收银员【差分约束】
2022-07-06 09:18:00 【小陈同学_】
题目:
一家超市要每天 24 24 24 小时营业,为了满足营业需求,需要雇佣一大批收银员。
已知不同时间段需要的收银员数量不同,为了能够雇佣尽可能少的人员,从而减少成本,这家超市的经理请你来帮忙出谋划策。
经理为你提供了一个各个时间段收银员最小需求数量的清单 R ( 0 ) , R ( 1 ) , R ( 2 ) , … , R ( 23 ) R(0),R(1),R(2),…,R(23) R(0),R(1),R(2),…,R(23)。
R ( 0 ) R(0) R(0) 表示午夜 00 : 00 00:00 00:00 到凌晨 01 : 00 01:00 01:00 的最小需求数量, R ( 1 ) R(1) R(1) 表示凌晨 01 : 00 01:00 01:00 到凌晨 02 : 00 02:00 02:00 的最小需求数量,以此类推。
一共有 N N N 个合格的申请人申请岗位,第 i 个申请人可以从 ti 时刻开始连续工作 8 8 8 小时。
收银员之间不存在替换,一定会完整地工作 8 8 8 小时,收银台的数量一定足够。
现在给定你收银员的需求清单,请你计算最少需要雇佣多少名收银员。
输入格式
第一行包含一个不超过 20 20 20 的整数,表示测试数据的组数。
对于每组测试数据,第一行包含 24 24 24 个整数,分别表示 R ( 0 ) , R ( 1 ) , R ( 2 ) , … , R ( 23 ) R(0),R(1),R(2),…,R(23) R(0),R(1),R(2),…,R(23)。
第二行包含整数 N。
接下来 N N N 行,每行包含一个整数 t i t_i ti。
输出格式
每组数据输出一个结果,每个结果占一行。
如果没有满足需求的安排,输出 No Solution。
数据范围
0 ≤ R ( 0 ) ≤ 1000 , 0≤R(0)≤1000, 0≤R(0)≤1000,
0 ≤ N ≤ 1000 , 0≤N≤1000, 0≤N≤1000,
0 ≤ t i ≤ 23 0≤t_i≤23 0≤ti≤23
输入样例:
1
1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
5
0
23
22
1
10
输出样例:
1
题目思路:
因为求最少,所以用最长路。
num[i]:第i时刻申请上岗的人数
x[i]:第i时刻实际上岗的人数
r[i]:第i时刻的最小需求
s[i]:从1到i中申请上岗的人数
第i个时刻可以由哪个时刻的人上岗: x [ i − 7 ] + x [ i − 6 ] + x [ i − 5 ] + . . . + x [ i ] x[i-7]+x[i-6]+x[i-5]+...+x[i] x[i−7]+x[i−6]+x[i−5]+...+x[i]
每个时刻申请上岗的人数肯定大于0: 0 < = x [ i ] < = n u m [ i ] 0<=x[i]<=num[i] 0<=x[i]<=num[i]
第i个时刻上岗的人数必须要大于等于r[i],所以 x [ i − 7 ] + x [ i − 6 ] + x [ i − 5 ] + . . . + x [ i ] > = r [ i ] x[i-7]+x[i-6]+x[i-5]+...+x[i]>=r[i] x[i−7]+x[i−6]+x[i−5]+...+x[i]>=r[i];
因为求的是一段的和,所以可以用前缀和求
转化为前缀和后: 0 < = x [ i ] < = n u m [ i ] 0<=x[i]<=num[i] 0<=x[i]<=num[i] -> 0 < = s [ i ] − s [ i − 1 ] < = n u m [ i ] 0<=s[i]-s[i-1]<=num[i] 0<=s[i]−s[i−1]<=num[i] ①
x [ i − 7 ] + x [ i − 6 ] + x [ i − 5 ] + . . . + x [ i ] > = r [ i ] x[i-7]+x[i-6]+x[i-5]+...+x[i]>=r[i] x[i−7]+x[i−6]+x[i−5]+...+x[i]>=r[i] -> s [ i ] − s [ i ] − 8 > = r [ i ] s[i]-s[i]-8>=r[i] s[i]−s[i]−8>=r[i] ②
因为时间是循环的24:00之后是1:00,所以要分情况讨论第二个公式i>=8 s [ i ] − s [ i − 8 ] > = r [ i ] s[i]-s[i-8]>=r[i] s[i]−s[i−8]>=r[i]i<8 s [ i ] + s [ 24 ] − s [ i + 16 ] > = r [ i ] s[i]+s[24]-s[i+16]>=r[i] s[i]+s[24]−s[i+16]>=r[i]
整理之后得
s [ i ] > = s [ i − 1 ] s[i]>=s[i-1] s[i]>=s[i−1] ①
s [ i − 1 ] > = s [ i ] − n u m [ i ] s[i-1]>=s[i]-num[i] s[i−1]>=s[i]−num[i] ②
s [ i ] > = s [ i − 8 ] + r [ i ] s[i]>=s[i-8]+r[i] s[i]>=s[i−8]+r[i] ③
s [ i ] = s [ i + 16 ] − s [ 24 ] + r [ i ] s[i]=s[i+16]-s[24]+r[i] s[i]=s[i+16]−s[24]+r[i] ④
因为差分约束的形式都是x[i]>=x[j]+c,在这里s[24]就是最终的答案,并且申请上岗人员为01000,所以我们可以枚举01000中的数来使s[24]变为常数
因为我们枚举的s[24],所以这个点已经固定了,然后可以利用这两个公式来固定这个点(c为枚举的答案)
s [ 24 ] > = c s[24]>=c s[24]>=c s [ 24 ] < = c s[24]<=c s[24]<=c -> s [ 24 ] > = s [ 0 ] + c s[24]>=s[0]+c s[24]>=s[0]+c s [ 24 ] < = s [ 0 ] + c s[24]<=s[0]+c s[24]<=s[0]+c
最终得出
s[i]>=s[i-1] ①
s[i-1]>=s[i]-num[i] ②
s[i]>=s[i-8]+r[i] ③
s[i]=s[i+16]-s[24]+r[i] ④
s[24]>=s[0]+c ⑤
s[0]>=s[24]-c ⑥
AC代码(C++):
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int N=30,M=100;
int n,t;
int h[N],e[M],ne[M],w[M],idx;
int dist[N];
int cnt[N];
bool st[N];
int num[N],r[N];
void add(int a,int b,int c){
w[idx]=c;
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
bool spfa(int c){
memset(h,-1,sizeof h);
idx=0;
memset(dist,-0x3f,sizeof dist);
memset(cnt,0,sizeof cnt);
memset(st,0,sizeof st);
for(int i=1;i<=24;i++){
add(i-1,i,0);
add(i,i-1,-num[i]);
if(i>=8) add(i-8,i,r[i]);
if(i<8) add(i+16,i,r[i]-c);
}
add(0,24,c),add(24,0,-c);
queue<int> q;
q.push(0);
dist[0]=0;
st[0]=true;
while(q.size()){
int t=q.front();
q.pop();
st[t]=false;
cnt[t]++;
if(cnt[t]>=N) return true;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(dist[j]<dist[t]+w[i]){
dist[j]=dist[t]+w[i];
if(!st[j]){
q.push(j);
st[j]=true;
}
}
}
}
return false;
}
int main(){
scanf("%d",&t);
while(t--){
memset(num,0,sizeof num);
for(int i=1;i<=24;i++) scanf("%d",&r[i]);
scanf("%d",&n);
for(int i=1;i<=n;i++){
int x;
scanf("%d",&x);
num[x+1]++;
}
bool f=true;
for(int i=0;i<=1000;i++){
if(!spfa(i)){
printf("%d\n",i);
f=false;
break;
}
}
if(f) printf("No Solution\n");
}
return 0;
}
边栏推荐
猜你喜欢

Theoretical derivation of support vector machine
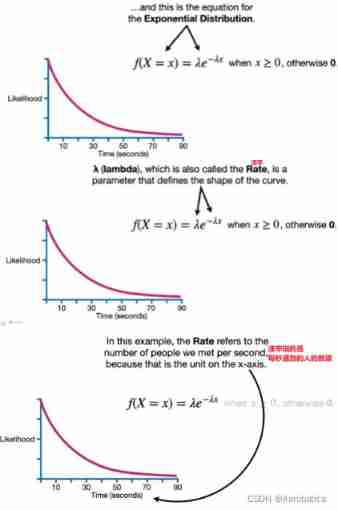
Expected value (EV)

服务未正常关闭导致端口被占用
Compilation principle: preprocessing of source program and design and implementation of lexical analysis program (including code)
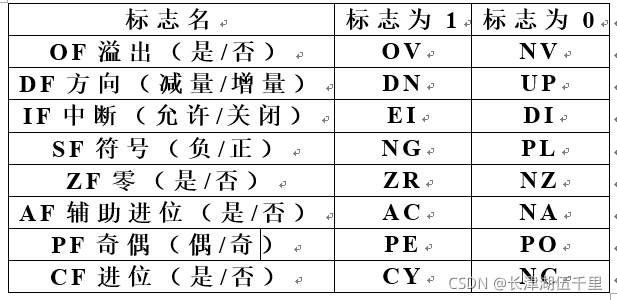
2021.11.10 compilation examination

341. Flatten nested list iterator
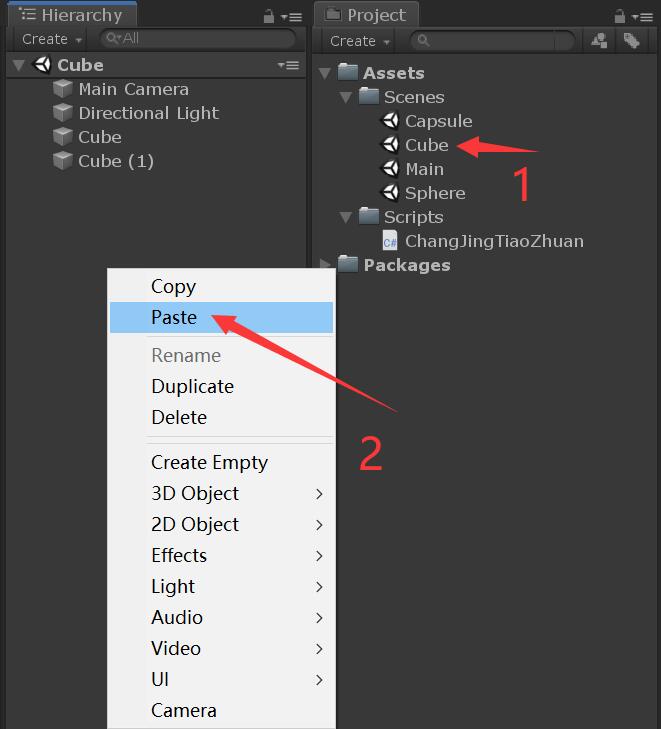
Unity场景跳转及退出
There is no red exclamation mark after SVN update
![[算法] 剑指offer2 golang 面试题10:和为k的子数组](/img/63/7422489d09a64ec9f0e79378761bf1.png)
[算法] 剑指offer2 golang 面试题10:和为k的子数组
The service robots that have been hyped by capital and the Winter Olympics are not just a flash in the pan
随机推荐
Minio file download problem - inputstream:closed
FairyGUI复选框与进度条的组合使用
Teach you to release a DeNO module hand in hand
The master of double non planning left the real estate company and became a programmer with an annual salary of 25W. There are too many life choices at the age of 25
What are the advantages of using SQL in Excel VBA
(1) Introduction Guide to R language - the first step of data analysis
Matlab读取GNSS 观测值o文件代码示例
【干货】提升RTK模糊度固定率的建议之周跳探测
單片機藍牙無線燒錄
(课设第一套)1-5 317号子任务 (100 分)(Dijkstra:重边自环)
Itext 7 生成PDF总结
[算法] 剑指offer2 golang 面试题9:乘积小于k的子数组
Theoretical derivation of support vector machine
Unity3D摄像机,键盘控制前后左右上下移动,鼠标控制旋转、放缩
地球围绕太阳转
RTKLIB: demo5 b34f.1 vs b33
[offer29] sorted circular linked list
SSD technical features
Combination of fairygui check box and progress bar
GPS高程拟合抗差中误差的求取代码实现