当前位置:网站首页>Expected value (EV)
Expected value (EV)
2022-07-06 12:22:00 【Aerobatics】
1. Expectations (Expected Value,EV)
Note source :StatQuest series :Expected Values, Main Ideas!!!
1.1 Expectation of discrete events
Start with a bet , The little man on the left of the picture below bets me , On the island StatLand Interview a resident of the island at random , If the resident has heard of movies Troll2, Then I lose to the villain 1dollar, If the resident has not heard of , Then I win 1dollar

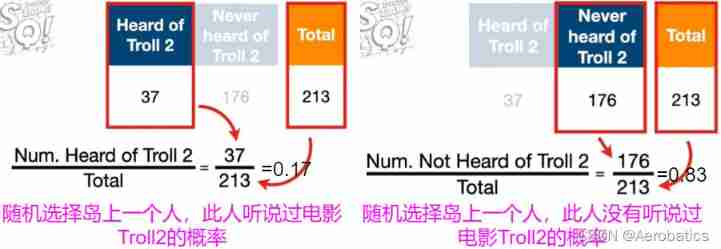
Let's count the movies we've heard of on the island Troll2 The number of people 、 I haven't heard of movies Troll2 The number of people 、 The total number of

Let's calculate that we have heard of movies Troll2 The proportion of the number of people in the total number of people on the island 、 I haven't heard of movies Troll2 The proportion of the number of people in the total number of people on the island
We will match the possible results of gambling with the statistical situation

No one wants to lose the bet , We fight with little people 100 Second gamble , We can predict how much money we can win or lose in the end
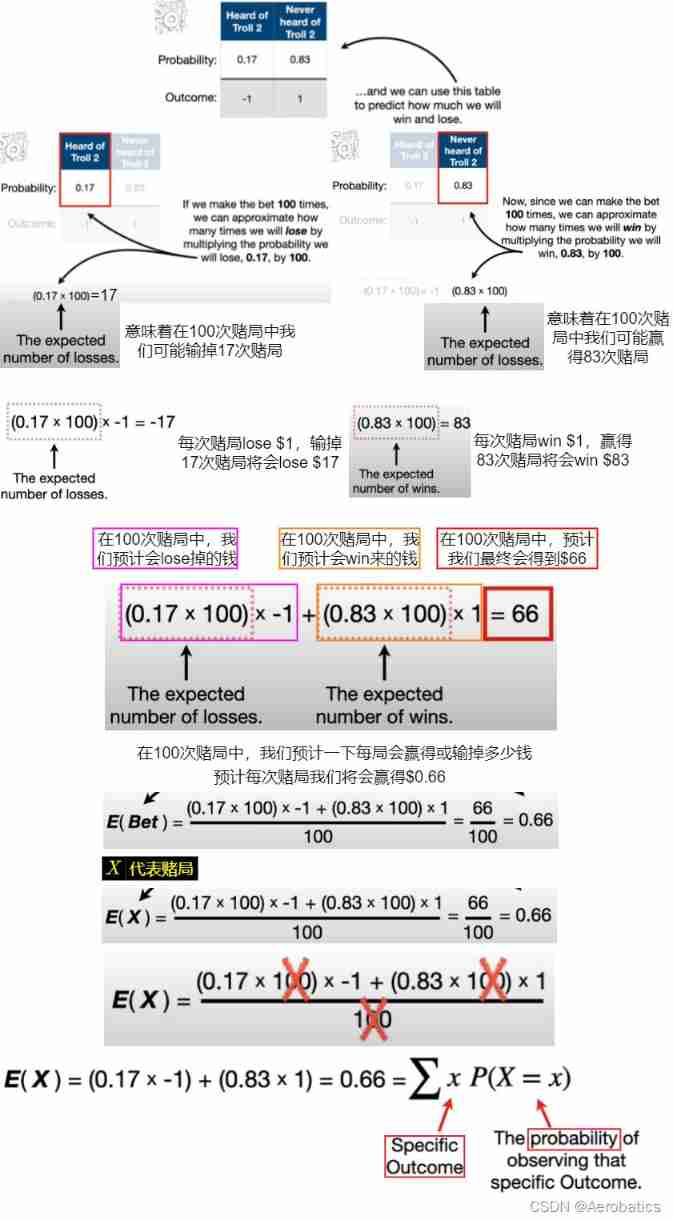
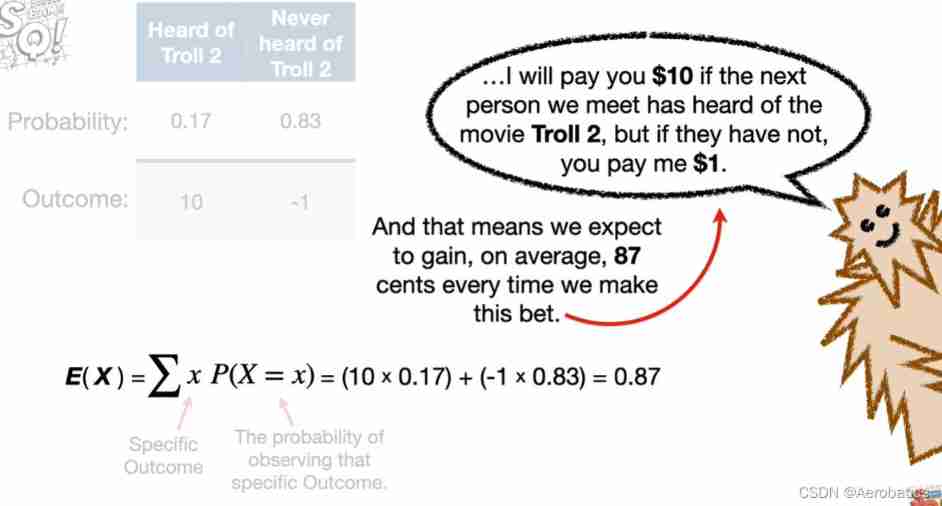
Suppose we bet more , Every time I win a bet, I will get 10dollar, If I lose, I will lose 1dollar
How much money can we win or lose in a lot of gambling ? Please calculate the expected value
1.2 Expectations for continuous events
Note source :Expected Values for Continuous Variables!!!
The little man walks on the road of the island , How long will it take to see someone ?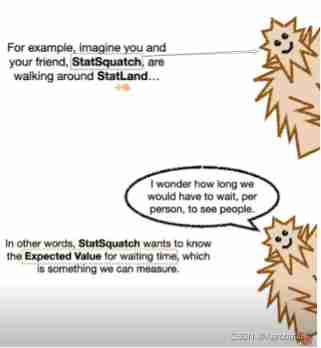
We use 10 Seconds as an interval , The results of an experiment are as follows :
At the beginning, I met 7 personal , After that 10 Seconds later, I encountered 4 personal , After that 20 Seconds later, I encountered 2 people , After that 30 Seconds later, I encountered 2 people , After that 50 Seconds later, I encountered 2 people , After that 70 Seconds later, I encountered 2 people
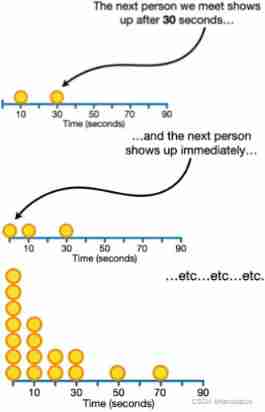
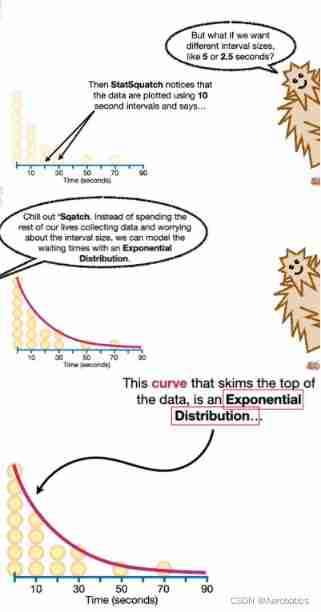
If you want to 5 Experiment at intervals of seconds ? If you want to 2.5 Experiment at intervals of seconds ? The smaller the time interval, the more comprehensive the experiment we get , Because you are at an interval of 10 Second experiment , If in the first place 5 Seconds met someone , You didn't count , Data loss , But we can't collect all the experimental data at intervals in our whole life , Because the time interval can be subdivided infinitely , From this we get continuous
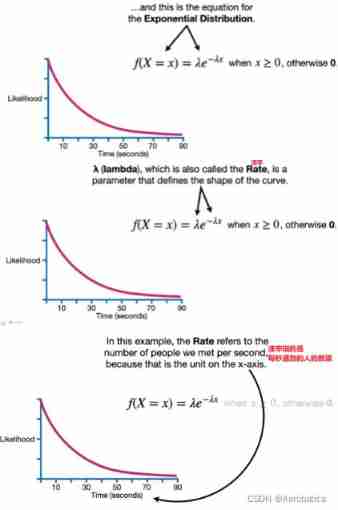
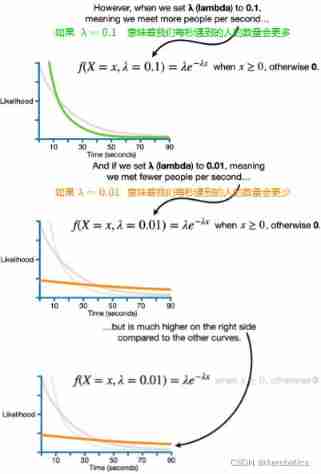
In this function of exponential distribution λ \lambda λ Represents the number of people encountered per second
In the above experiment , When λ = 0.05 \lambda=0.05 λ=0.05 when , The curve conforms to the current experimental data
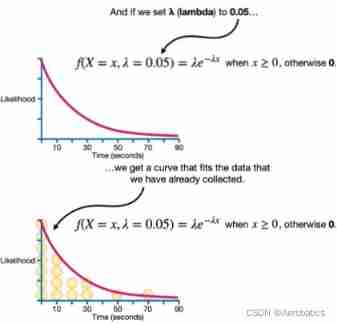
We try to change λ \lambda λ Value
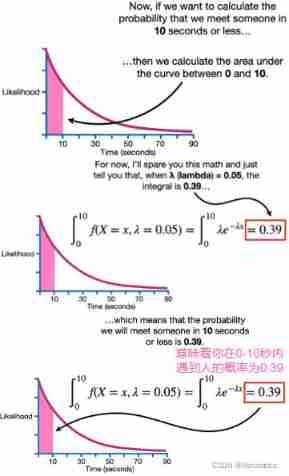
Let's calculate 0-10 The probability of meeting someone in seconds
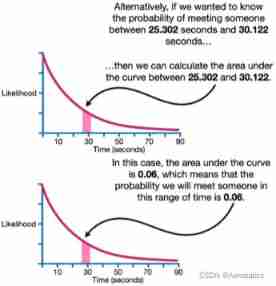
Allied , Let's calculate 25.302-30.122 The probability of meeting someone in seconds
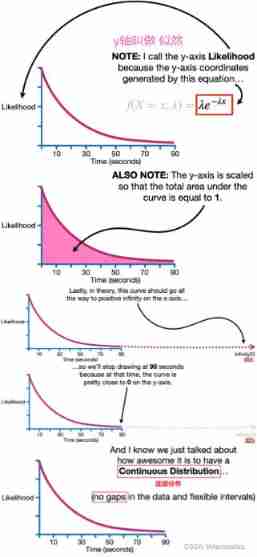
Notice about this exponential distribution
As mentioned below y Axis It's called likelihood (Likelihood)
The reasons are detailed in :Maximum Likelihood for the Exponential Distribution, Clearly Explained!!!
Compare the expected value of discrete variables with the expected value of continuous variables
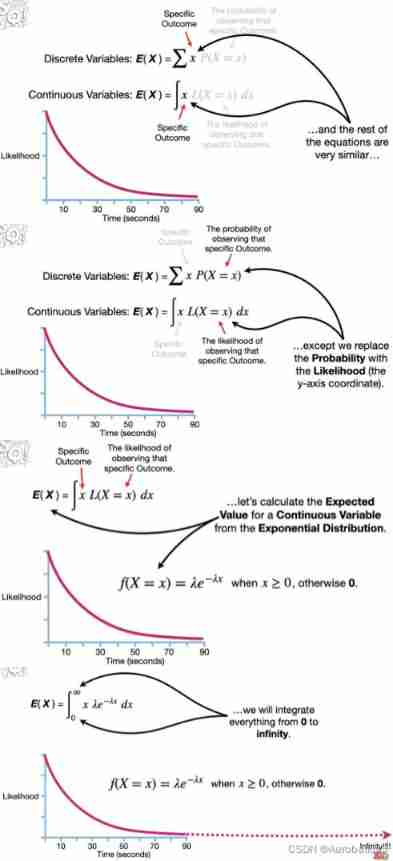
Next, we calculate the expected value of continuous variables

边栏推荐
- Gravure sans fil Bluetooth sur micro - ordinateur à puce unique
- Arduino gets the length of the array
- Esp8266 connects to onenet cloud platform (mqtt) through Arduino IDE
- 單片機藍牙無線燒錄
- Time slice polling scheduling of RT thread threads
- Stm32f1+bc20+mqtt+freertos system is connected to Alibaba cloud to transmit temperature and humidity and control LED lights
- Kconfig Kbuild
- Important methods of array and string
- Analysis of charging architecture of glory magic 3pro
- MySQL時間、時區、自動填充0的問題
猜你喜欢

Fashion Gen: the general fashion dataset and challenge paper interpretation & dataset introduction
ESP8266使用arduino连接阿里云物联网

Stm32f1+bc20+mqtt+freertos system is connected to Alibaba cloud to transmit temperature and humidity and control LED lights

Esp8266 uses Arduino to connect Alibaba cloud Internet of things

基於Redis的分布式ID生成器
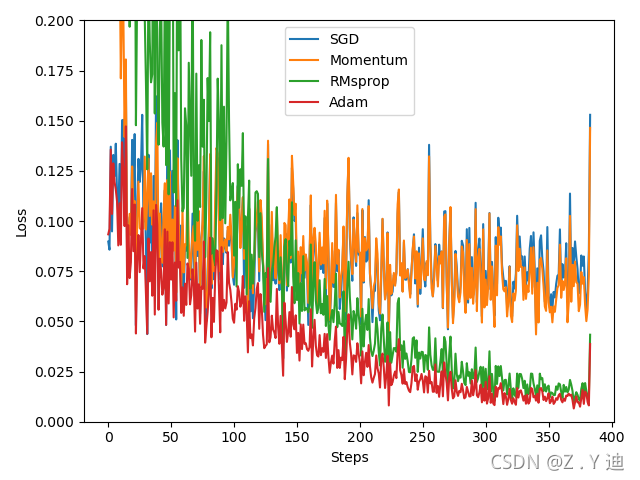
Pytorch four commonly used optimizer tests
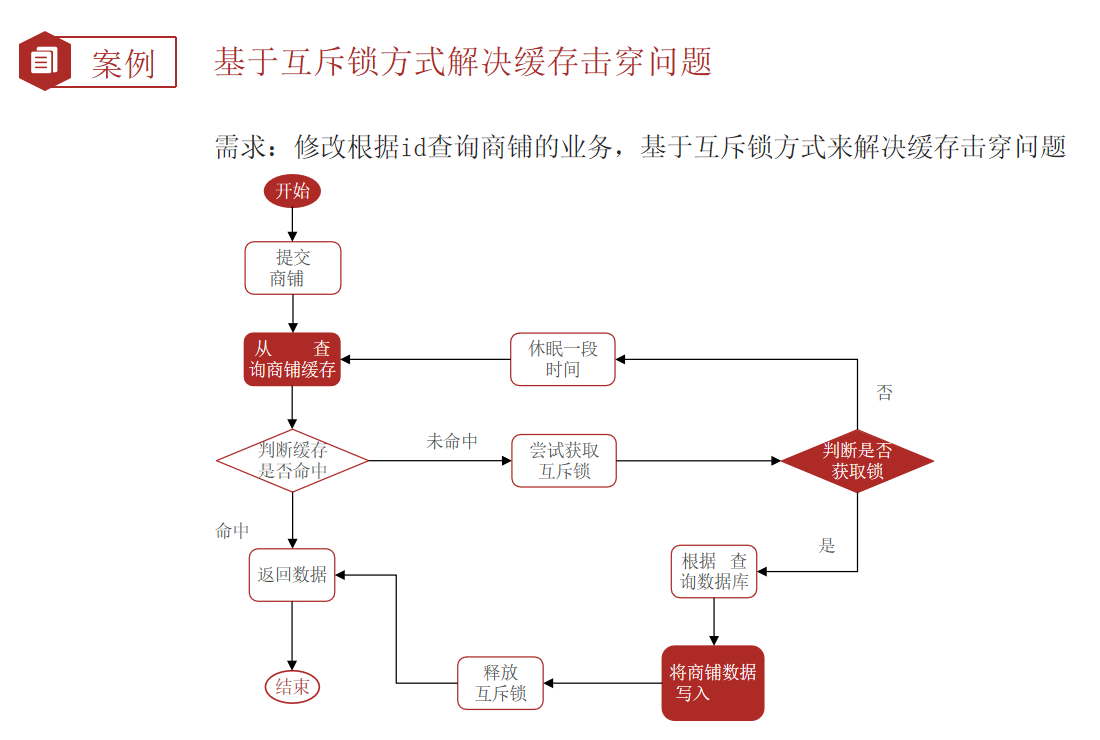
Redis 缓存更新策略,缓存穿透、雪崩、击穿问题

Basic operations of databases and tables ----- creating data tables
Redis based distributed locks and ultra detailed improvement ideas
JS regular expression basic knowledge learning
随机推荐
單片機藍牙無線燒錄
ESP8266使用arduino连接阿里云物联网
数据库课程设计:高校教务管理系统(含代码)
Common properties of location
RuntimeError: cuDNN error: CUDNN_ STATUS_ NOT_ INITIALIZED
I2C bus timing explanation
AMBA、AHB、APB、AXI的理解
Minio文件下载问题——inputstream:closed
程序设计大作业:教务管理系统(C语言)
Pat 1097 duplication on a linked list (25 points)
Basic operations of databases and tables ----- classification of data
MySQL time, time zone, auto fill 0
Walk into WPF's drawing Bing Dwen Dwen
Arduino JSON data information parsing
ESP learning problem record
Redis 缓存更新策略,缓存穿透、雪崩、击穿问题
Reno7 60W super flash charging architecture
Basic operations of databases and tables ----- modifying data tables
Analysis of charging architecture of glory magic 3pro
小天才电话手表 Z3工作原理