E-commerce data analysis -- salary prediction (linear regression)

E-commerce data analysis – Salary forecast （ Linear regression ）

Data analysis process ：

1. Clear purpose
2. get data
3. Data exploration and preprocessing
4. Analyze the data
5. Come to the conclusion
6. Verification conclusion
7. Result presentation

Linear regression ： Linear regression is to use regression analysis in mathematical statistics , A statistical analysis method to determine the quantitative relationship between two or more variables , It's widely used . It is expressed in the form of y = w’x+e,e The mean value of error is 0 Is a normal distribution . In regression analysis , Include only one independent variable and one dependent variable , And the relationship between them can be approximately expressed by a straight line , This kind of regression analysis is called univariate linear regression analysis . If the regression analysis includes two or more independent variables , And the relationship between dependent variable and independent variable is linear , It is called multiple linear regression analysis .（ Commonly used in demand forecasting 、 Sales forecast 、 Ranking forecast ）

Univariate linear regression equation ：$y=b+aX$
b Is the intercept ,a Is the slope of the regression line
Multiple linear regression equation ：$y=b0+b1X1+b2X2+...+bnXn$
$b0byoftenCountterm,b1,b2,b3,bnbyyYesShould\; beAndX1,X2,X3..XnOfpartialreturnreturnsystemCount.$

skearn library - Linear regression （LinearRegression）

Specific parameter interpretation and call method ：

from sklearn.linear_model import LinearRegression
LinearRegression(fit_intercept=True,normalize=False.copy_x=True,n_jobs=1)

Parameter meaning ：
1、fit_intercept: Boolean value , Specify whether to calculate the intercept in linear regression , namely b value . If False, Then don't count b value .
2、normalize： Boolean value . If False, Then the training samples will be normalized .
3、copy_x： Boolean value . If True, Will copy a copy of training data ,
4、n_jobs： An integer . Specified when tasks are parallel CPU Number . If the value is -1 Then use all available CPU.

attribute ：
1、coef_: The weight vector
2、intercept_: intercept b value

Method ：
1、fit(X,y): Training models
2、predict(X): Use the model of training number to predict , And return the predicted value .
3、score(X,y): Return the score of prediction performance . The formula is ：score=(1-u/v)
among u=((y_ture-y_pred)**2).sum(),v=((y_true-y_ture.mean())**2).sum()
score The maximum is 1, But it may be negative （ The prediction effect is too poor ）.score The bigger it is , The better the prediction performance .

Salary prediction case realization

Univariate linear regression （ Working years and salary ）, The data is shown in the figure .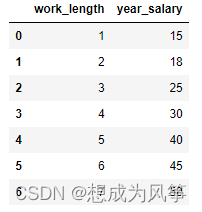

# Call the library necessary for data analysis 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model  # Linear model 
# Import data 
single_variable = pd.read_csv(r"E:\ Data analysis \ingle_variable.csv")
print(single_variable) # View the data 
print(single_variable.shape)
print(single_variable.isnull().any())  # Whether there are missing values 

# Prepare the data 
length = len(single_variable['work_length'])
X = np.array(single_variable['work_length']).reshape([length,1])
Y = np.array(single_variable['year_salary'])
# Plot observation data 
# Draw a scatter plot ,X,Y, Set the color , Mark parameters such as point style and transparency 
plt.scatter(X,Y,60,color='blue',marker='o',linewidth=3,alpha=0.8)
# add to x Axis title 
plt.xlabel('work years')
# add to y Axis title 
plt.ylabel('year salary')
# Add chart title 
plt.title('work years and year salary')
# Set the background grid line color , style , Size and transparency 
plt.grid(color='#95a5a6',linestyle='--', linewidth=1,axis='both',alpha=0.4)
# Show chart 
plt.show()

# Call the linear regression model 
linear=linear_model.LinearRegression()
linear.fit(X,Y)
# Check intercept and coefficient 
print(linear.coef_ )
print(linear.intercept_)
# Check the fitting effect score 
print(linear.score(X,Y))

# New data forecast 
x_new = np.array(8).reshape(1, -1)
y_pred =linear.predict(x_new)
print(y_pred)
# Finally it is concluded that  y = ax+b

Multiple linear regression （ Years of service 、 place 、 educational level 、 Grade and salary ）, The data is shown in the figure .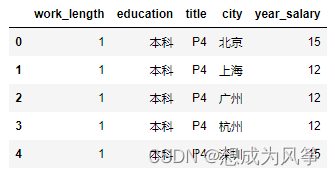

# Call the library necessary for data analysis 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model  # Linear model 
# Import data 
many_variable = pd.read_csv(r"E:\ Data analysis \many_variable.csv")
print(many_variable) # View the data 
print(many_variable.shape)
print(many_variable.isnull().any())  # Whether there are missing values 
# Data processing 
many_variable['education']=many_variable['education'].replace([' Undergraduate ',' Graduate student '],
                    [1,2])
many_variable['city']=many_variable['city'].replace([' Beijing ',' Shanghai ',' Guangzhou ',' Hangzhou ',' Shenzhen '],
                    [1,2,3,4,5])
many_variable['title']=many_variable['title'].replace(['P4','P5','P6','P7'],
                    [1,2,3,4])
# View the data 
print(many_variable)
# Prepare the data 
x = np.array(many_variable[['work_length','education','title','city']])
y = np.array(many_variable['year_salary'])
# Sharding data sets （ Training set and test set ）
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(x,y,test_size=0.4,random_state=1)
# Call the linear regression model 
linear2 = linear_model.LinearRegression()
linear2.fit(X_train,y_train)
# Check intercept and coefficient 
print(linear2.coef_ )
print(linear2.intercept_)
# Check the fitting effect score 
print(linear2.score(X,Y))

# New data forecast 
y_pred =list(linear2.predict(X_test))
print(y_pred)
# Finally it is concluded that  y=1.35+1.1*work_length+5.19*education+5.92*title+0.09*city