当前位置:网站首页>[combinatorics] exponential generating function (example 2 of solving multiple set permutation with exponential generating function)
[combinatorics] exponential generating function (example 2 of solving multiple set permutation with exponential generating function)
2022-07-03 18:20:00 【Programmer community】
List of articles
- One 、 Example of solving multiple set permutation with exponential generating function 2
Reference blog : Look in order
- 【 Combinatorial mathematics 】 Generating function Brief introduction ( Generating function definition | Newton's binomial coefficient | Common generating functions | Related to constants | Related to binomial coefficient | Related to polynomial coefficients )
- 【 Combinatorial mathematics 】 Generating function ( Linear properties | Product properties )
- 【 Combinatorial mathematics 】 Generating function ( Shift property )
- 【 Combinatorial mathematics 】 Generating function ( The nature of summation )
- 【 Combinatorial mathematics 】 Generating function ( Commutative properties | Derivative property | Integral properties )
- 【 Combinatorial mathematics 】 Generating function ( Summary of nature | Important generating functions ) *
- 【 Combinatorial mathematics 】 Generating function ( Generate function examples | Given the general term formula, find the generating function | Given the generating function, find the general term formula )
- 【 Combinatorial mathematics 】 Generating function ( Generate function application scenarios | Solving recursive equations using generating functions )
- 【 Combinatorial mathematics 】 Generating function ( Use the generating function to solve multiple sets r Combinatorial number )
- 【 Combinatorial mathematics 】 Generating function ( Use generating function to solve the number of solutions of indefinite equation )
- 【 Combinatorial mathematics 】 Generating function ( Examples of using generating functions to solve the number of solutions of indefinite equations )
- 【 Combinatorial mathematics 】 Generating function ( Examples of using generating functions to solve the number of solutions of indefinite equations 2 | Extended to integer solutions )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | disorder | Orderly | Allow repetition | No repetition | Unordered and unrepeated splitting | Unordered repeated split )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | Unordered non repeated split example )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | Basic model of positive integer splitting | Disorderly splitting with restrictions )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | Repeated ordered splitting | Do not repeat orderly splitting | Proof of the number of repeated ordered splitting schemes )
- 【 Combinatorial mathematics 】 Exponential generating function ( The concept of exponential generating function | Permutation number exponential generating function = General generating function of combinatorial number | Example of exponential generating function )
- 【 Combinatorial mathematics 】 Exponential generating function ( Properties of exponential generating function | The exponential generating function solves the arrangement of multiple sets )
- 【 Combinatorial mathematics 】 Exponential generating function ( Example of solving multiple set permutation with exponential generating function )
One 、 Example of solving multiple set permutation with exponential generating function 2
Use white Red Blue Coloring
n
n
n Lattice , The number of white colors is even , Find the number of coloring schemes
This is a The problem of permutation , When different squares are colored and exchanged , It becomes a different solution ,
Red , Blue Coloring , There is no limit to , The number of colors can be
0
,
1
,
2
,
3
,
4
,
⋯
0, 1,2,3,4,\cdots
0,1,2,3,4,⋯
white Coloring , The number of colors is even , The number of colors is
0
,
2
,
4
,
6
,
8
,
⋯
0, 2, 4, 6, 8 , \cdots
0,2,4,6,8,⋯
Red , Blue Number of colors
0
,
1
,
2
,
3
,
4
,
⋯
0, 1,2,3,4,\cdots
0,1,2,3,4,⋯ Sequence , The corresponding generating function item is :
x
0
0
!
+
x
1
1
!
+
x
2
2
!
⋯
=
1
+
x
+
x
2
2
!
+
⋯
\cfrac{x^0}{0!} + \cfrac{x^1}{1!} + \cfrac{x^2}{2!} \cdots = 1 + x + \cfrac{x^2}{2!} + \cdots
0!x0+1!x1+2!x2⋯=1+x+2!x2+⋯
white Number of colors
0
,
2
,
4
,
6
,
8
,
⋯
0, 2, 4, 6, 8 , \cdots
0,2,4,6,8,⋯ Sequence , The corresponding generating function item is :
x
0
0
!
+
x
2
2
!
+
x
4
4
!
⋯
=
1
+
x
2
2
!
+
x
4
4
!
+
⋯
\cfrac{x^0}{0!} + \cfrac{x^2}{2!} + \cfrac{x^4}{4!} \cdots = 1+ \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots
0!x0+2!x2+4!x4⋯=1+2!x2+4!x4+⋯
The exponential generating function of the number of the above coloring schemes is :
G
e
(
x
)
=
(
1
+
x
+
x
2
2
!
+
⋯
)
(
1
+
x
+
x
2
2
!
+
⋯
)
(
1
+
x
2
2
!
+
x
4
4
!
+
⋯
)
G_e(x) = (1 + x + \cfrac{x^2}{2!} + \cdots) (1 + x + \cfrac{x^2}{2!} + \cdots) (1+ \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots)
Ge(x)=(1+x+2!x2+⋯)(1+x+2!x2+⋯)(1+2!x2+4!x4+⋯)
among
1
+
x
+
x
2
2
!
+
⋯
1 + x + \cfrac{x^2}{2!} + \cdots
1+x+2!x2+⋯ Sure It's written in
e
x
e^x
ex form ;
among
1
+
x
2
2
!
+
x
4
4
!
+
⋯
1+ \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots
1+2!x2+4!x4+⋯ We can write it in the following form :
1
+
x
2
2
!
+
x
4
4
!
+
⋯
=
1
2
(
e
x
+
e
−
x
)
1+ \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots = \cfrac{1}{2}(e^x + e^{-x})
1+2!x2+4!x4+⋯=21(ex+e−x)
e
x
+
e
−
x
e^x + e^{-x}
ex+e−x Add up , The sign of odd power is opposite , Direct appointment , Even power Double the original , So multiply it outside
1
2
\cfrac{1}{2}
21 ;
Put the above
e
x
e^x
ex and
1
2
(
e
x
+
e
−
x
)
\cfrac{1}{2}(e^x + e^{-x})
21(ex+e−x) Replace the Exponential generating function ;
G
e
(
x
)
=
(
1
+
x
+
x
2
2
!
+
⋯
)
(
1
+
x
+
x
2
2
!
+
⋯
)
(
1
+
x
2
2
!
+
x
4
4
!
+
⋯
)
G_e(x) = (1 + x + \cfrac{x^2}{2!} + \cdots) (1 + x + \cfrac{x^2}{2!} + \cdots) (1+ \cfrac{x^2}{2!} + \cfrac{x^4}{4!} + \cdots)
Ge(x)=(1+x+2!x2+⋯)(1+x+2!x2+⋯)(1+2!x2+4!x4+⋯)
=
1
2
(
e
x
+
e
−
x
)
(
e
x
)
(
e
x
)
\ \ \ \ \ \ \ \ \ \ \ \, =\cfrac{1}{2}(e^x + e^{-x})(e^x )(e^x)
=21(ex+e−x)(ex)(ex)
=
1
2
e
3
x
+
1
2
e
x
\ \ \ \ \ \ \ \ \ \ \ \, =\cfrac{1}{2}e^{3x} + \cfrac{1}{2}e^{x}
=21e3x+21ex
take
1
2
e
x
\cfrac{1}{2}e^{x}
21ex Expand to
1
2
(
1
+
x
+
x
2
2
!
+
⋯
)
=
1
2
∑
n
=
0
∞
x
n
n
!
\cfrac{1}{2}(1 + x + \cfrac{x^2}{2!} + \cdots)=\cfrac{1}{2}\sum\limits_{n=0}^\infty \cfrac{x^n}{n!}
21(1+x+2!x2+⋯)=21n=0∑∞n!xn
take
1
2
e
3
x
\cfrac{1}{2}e^{3x}
21e3x Expand to
1
2
(
1
+
3
x
+
(
3
x
)
2
2
!
+
⋯
)
=
1
2
∑
n
=
0
∞
3
n
x
n
n
!
\cfrac{1}{2}(1 + 3x + \cfrac{(3x)^2}{2!} + \cdots)=\cfrac{1}{2}\sum\limits_{n=0}^\infty \cfrac{3^nx^n}{n!}
21(1+3x+2!(3x)2+⋯)=21n=0∑∞n!3nxn
=
1
2
∑
n
=
0
∞
3
n
x
n
n
!
+
1
2
∑
n
=
0
∞
x
n
n
!
\ \ \ \ \ \ \ \ \ \ \ \, =\cfrac{1}{2}\sum\limits_{n=0}^\infty \cfrac{3^nx^n}{n!} + \cfrac{1}{2}\sum\limits_{n=0}^\infty \cfrac{x^n}{n!}
=21n=0∑∞n!3nxn+21n=0∑∞n!xn
=
∑
n
=
0
∞
3
n
+
1
2
⋅
x
n
n
!
\ \ \ \ \ \ \ \ \ \ \ \, =\sum\limits_{n=0}^\infty \cfrac{3^n + 1}{2} \cdot \cfrac{x^n}{n!}
=n=0∑∞23n+1⋅n!xn
x
n
n
!
\cfrac{x^n}{n!}
n!xn The coefficient before is
3
n
+
1
2
\cfrac{3^n + 1}{2}
23n+1
therefore white Red Blue Coloring
n
n
n Lattice , White is even , The coloring scheme has
3
n
+
1
2
\cfrac{3^n + 1}{2}
23n+1 Kind of ;
边栏推荐
- How to draw non overlapping bubble chart in MATLAB
- 分布式的任务分发框架-Gearman
- Nodejs (01) - introductory tutorial
- An academic paper sharing and approval system based on PHP for computer graduation design
- Fedora 21 安装 LAMP 主机服务器
- OpenSSL的SSL/BIO_get_fd
- [tutorial] build your first application on coreos
- Codeforces Round #803 (Div. 2) C. 3SUM Closure
- Design limitations of structure type (struct)
- Mature port AI ceaspectus leads the world in the application of AI in terminals, CIMC Feitong advanced products go global, smart terminals, intelligent ports, intelligent terminals
猜你喜欢
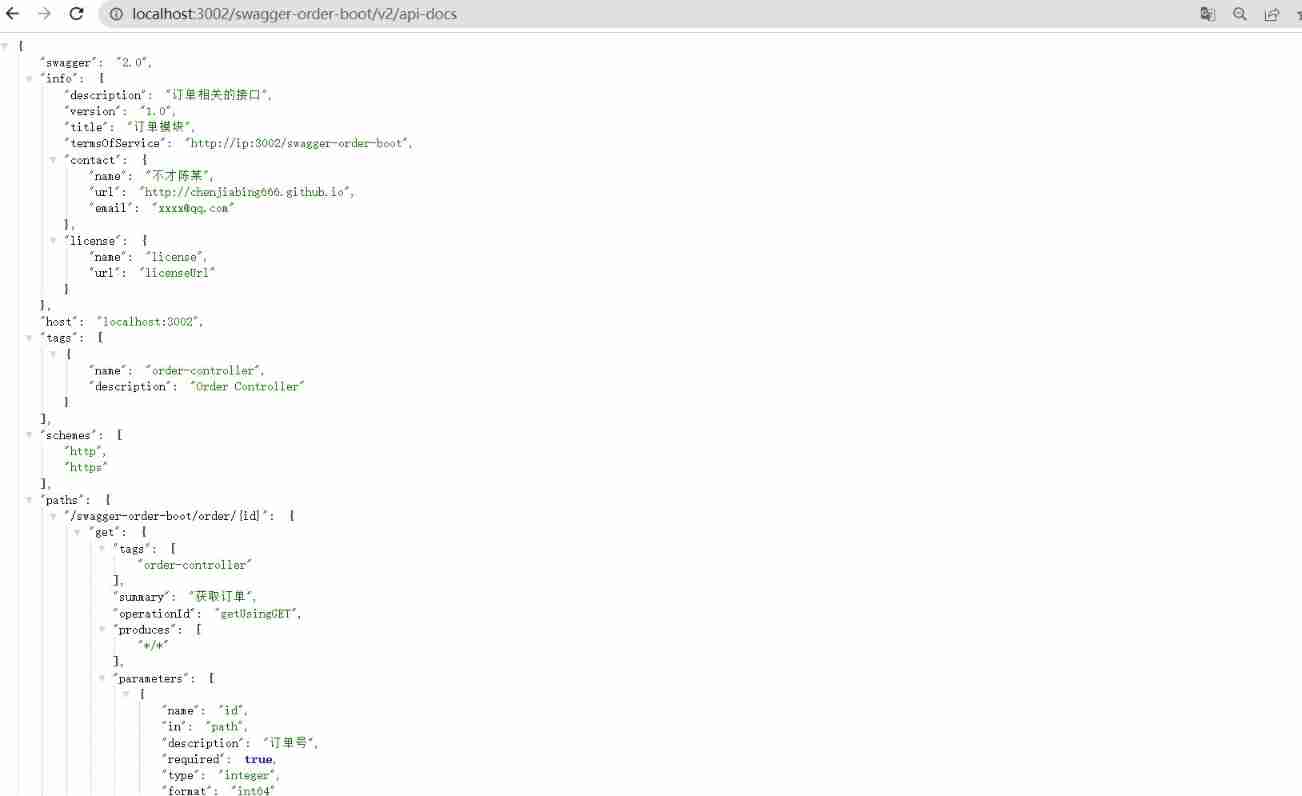
How do microservices aggregate API documents? This wave of operation is too good

Install apache+php+mysql+phpmyadmin xampp and its error resolution
On Data Mining
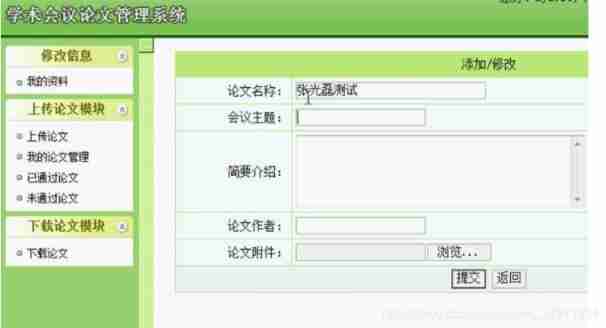
An academic paper sharing and approval system based on PHP for computer graduation design
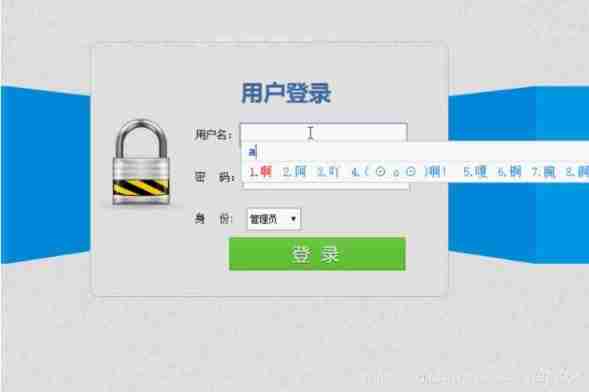
Computer graduation project PHP library book borrowing management system

Investigation on the operation prospect of the global and Chinese Anti enkephalinase market and analysis report on the investment strategy of the 14th five year plan 2022-2028
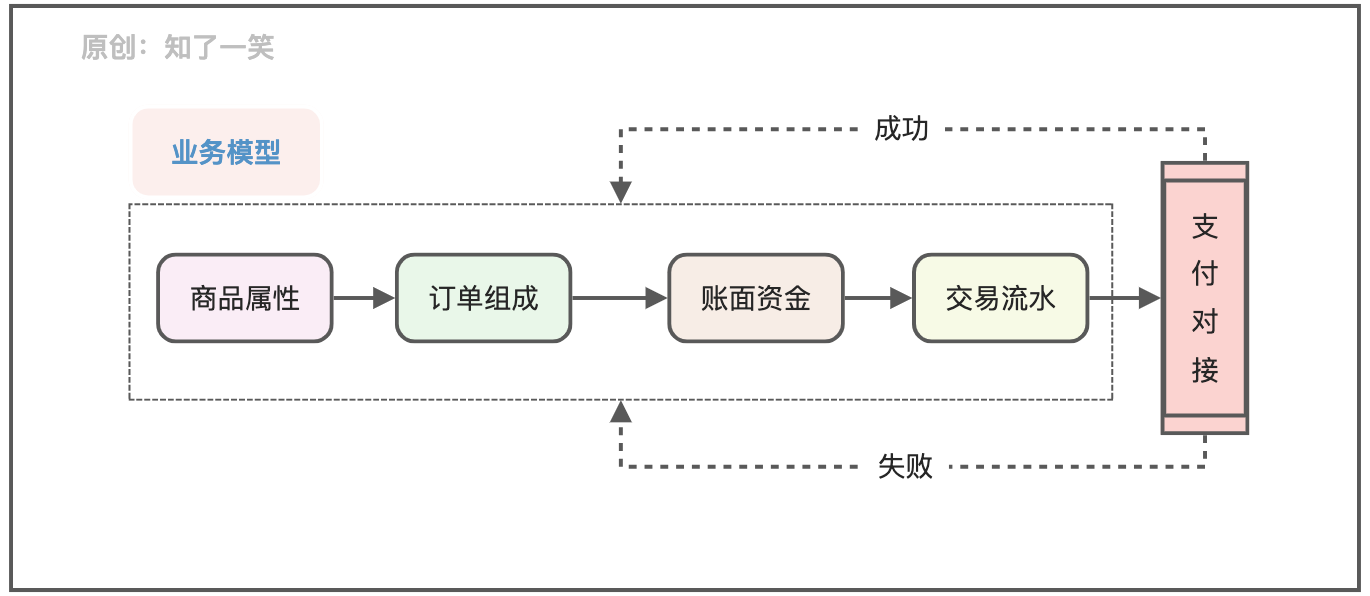
Talk about the design and implementation logic of payment process
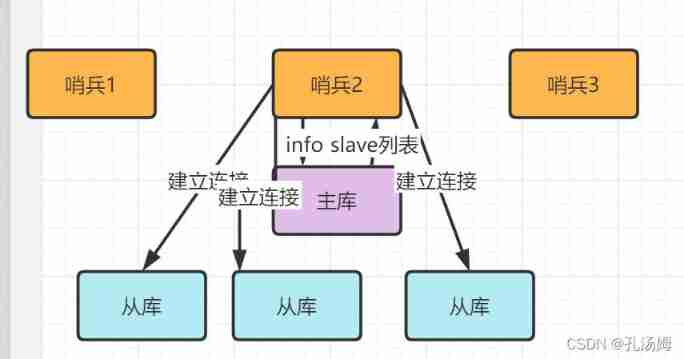
Redis core technology and practice - learning notes (VIII) sentinel cluster: sentinel hung up

2022-2028 global solid phase extraction column industry research and trend analysis report

Mature port AI ceaspectus leads the world in the application of AI in terminals, CIMC Feitong advanced products go global, smart terminals, intelligent ports, intelligent terminals
随机推荐
Redis core technology and practice - learning notes (IX): slicing cluster
一入“远程”终不悔,几人欢喜几人愁。| 社区征文
Closure and closure function
OpenSSL的SSL/BIO_get_fd
How do microservices aggregate API documents? This wave of operation is too good
企业级自定义表单引擎解决方案(十二)--表单规则引擎2
How to expand the capacity of golang slice slice
[linux]centos 7 reports an error when installing MySQL "no package MySQL server available" no package ZABBIX server MySQL available
Five problems of database operation in commodity supermarket system
Research Report on competitive strategy Outlook Analysis and investment strategic planning of China's smart home equipment industry, 2022-2028
[combinatorics] generating function (generating function application scenario | using generating function to solve recursive equation)
Market demand survey and marketing strategy analysis report of global and Chinese pet milk substitutes 2022-2028
PHP MySQL reads data
PHP MySQL Update
PHP MySQL inserts data
2022-2028 global plasmid DNA cdmo industry research and trend analysis report
Research Report on investment trends and development planning of China's thermal insulation material industry, 2022-2028
2022-2028 global sepsis treatment drug industry research and trend analysis report
聊聊支付流程的设计与实现逻辑
2022-2028 global lithium battery copper foil industry research and trend analysis report