当前位置：网站首页>Linear programming matlab

It refers to the proportion between quantity and quantity 、 In a straight line , Represent regular and smooth motion in space and time , The first derivative is constant

nonlinear (non-linear)：

It means not in proportion 、 A non-linear relationship , Represents irregular movement and mutation , The first derivative is not constant .

A linear example ：

data ： Salary and age （2 Features ）

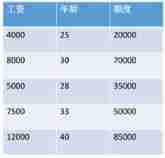
The goal is ： Predict how much the bank will lend me （ label ）

consider ： Both salary and age will affect the final result of bank loans , How much influence do they have respectively ？（ Parameters ）

Popular explanation ：

x1,x2 It's our two characteristics （ Age 、 Wages ）,y It's how much money the bank will eventually lend us

Find the most suitable line （ Imagine a high dimension ） To best fit our data points

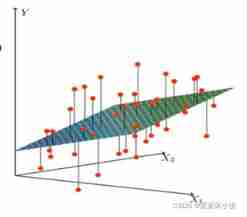
Here comes the mathematical form

Two 、 Mathematical form expression of concept

Given data set ：

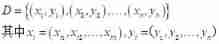
Matrix form of data ：

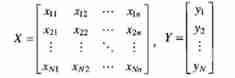
Linear model (linear model) Try to learn a function to predict through the linear combination of attribute combination , namely

use Vector form It's written in :

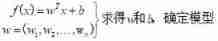
Linear regression (linear regression) Try to learn a linear model to predict the real value output mark as accurately as possible

3、 ... and 、 determine w and b

For discrete attributes ：

If between attributes There is “ order ” Relationship , It can be converted into continuous values by continuity .

If between attributes non-existent “ order ” Relationship , It's translated into k Dimension vector .

1. Read or input data

matlab No need to import libraries , Direct reference function csvread Read csv Data files

Let's first look at csv Data import

%  Reference function  csvread  Read csv Data files 

data = csvread(' route ',1,0) # From the second line , The first 0 Column read data

After reading the data, the sum is X, What is the Y

# matlab from 1 Start counting , As it is 
X = data[:,1:4]  # 1 To 4 List all the data, that is, the actual 1 To 4 Column 
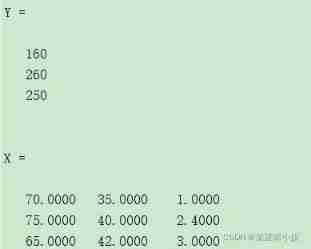
Y = data[:, 6]  #  The first 6 List all the data, that is, the actual number 6 Column

Next Let's see what we build matrix How to read data

Y=[160
   260
   250];

X=[70,35,1
 75,40,2.4
 65,42,3];

return ：

Speaking of matrices , By the way

Knowledge about creating matrices ：
(1) ones() function ： All are 1 Matrix ,ones(n)： produce n*n The whole of dimension 1 matrix ,ones(m,n)： produce m*n The whole of dimension 1 matrix ;
(2) zeros() function ： All are 0 Matrix ;
(3) rand() function ： Produced in （0,1） Interval uniformly distributed random matrix ;
(4) eye() function ： Generate unit matrix ;
(5) randn() function ： The average production is 0, The variance of 1 Standard normal distribution random matrix .

2. normalization 、 Standardization

2.1 mean value

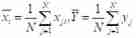
# MATLAB Direct reference mean() Function is good 
X_mean = mean(X)
Y_mean = mean(Y)

1. mean: Calculate the vector mean .mean(x,1) Column vector mean ,mean(x,2) Row vector mean . mean2(x) Matrix mean .
2. std： Calculate the mean square deviation of the vector ,std(x,0,1) Column vector mean square deviation ,std(x,0,2) Mean square deviation of row vector . std2(x) Matrix mean square deviation
3. var： Calculate vector variance ,var(x)
4. sse： The sum of the squares of the errors ,sse(x). The more close to 0, It shows that the better the fitting , The more successful the data prediction .
5. mse： Sum of squares of mean square deviation ,mse(x)=sse(x)/N. It means the same thing sse
6. R-square： Determine the coefficient . The coefficient of determination represents the quality of a fitting through the change of data . From the above expression, we can know “ Determine the coefficient ” The normal value range of is [0 1], The closer the 1, Show that the variables of the equation are y The better the ability to explain , This model fits the data well .

To be sure w and b, First, we should decide whether to normalize or standardize the data according to the situation

2.2 normalization

% normalization 

X=[70,35,1
 75,40,2.4
 65,42,3];
for X=X
    MappedX = (X-min(X))/(max(X)-min(X))
end

% Use functions mapminmax
% default map The scope is [-1, 1], So if you need to [0, 1], Then provide parameters in such a format :

MappedData = mapminmax(OriginalData, 0, 1);

%  Normalize by line only , If it's a matrix , Then each row is normalized , If you need to normalize the entire matrix 

FlattenedData = OriginalData(:)'; %  Expand the matrix into a column , Then transpose to one line .
MappedFlattened = mapminmax(FlattenedData, 0, 1); %  normalization .

%  Restore to the original matrix form . There is no need to transpose back here , because reshape It happens to be reordering by column 
MappedData = reshape(MappedFlattened, size(OriginalData));

2.3 Standardization

% z-score  Standardization 
%  The new data =（ The original data - mean value ）/ Standard deviation 
%  After standardization ,X The value range of the element in is a real number .

X=zscore(X)

3. solve w and b

1. Solve the equation directly

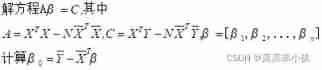
N = length(Y);

A = X'*X-(N*X_mean'*X_mean);
C=X'*Y - (N*X_mean'*Y_mean);
B = (A^-1*C).'

2. Least square method （least square method） solve ：

Put the data set D To express as a m*(d+1) Matrix of size X, Each line corresponds to an example , Change career d The elements correspond to the... Of the example d Attribute values , It is better to set an element to 1, namely

A=[1 2 3;4 5 6;7 8 9];
B = ones(3,1) % Generate 3 That's ok 1 Column 1 matrix 
% B=[1;1;1];  % Three lines in all , use “;” Separate 
A_column=[A B];
display(A_column);% Output results

When X^TX Is a full rank matrix (full-rank matrix) Or walking matrix (positive definite matrix) when , Make

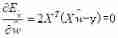
obtain

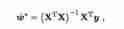
w = (X'*X)^-1*X'*Y % The coefficient of the variable 
w0 = Y_mean - X_mean*w % constant

among (X^TX)^-l It's a matrix (X^TX) The inverse matrix . Make xi = (xi ,l) , Then the final multiple linear regression model is

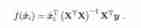
YY = X*w+w0 %Y The estimate of

4. Evaluating regression models

% Sum of squares of deviations 
S = var(Y);
fprintf(' Sum of squares of deviations S=：%d\n',S)
% Sum of regression squares 
U = var(YY);
fprintf(' Sum of regression squares U=：%d\n',U)
% The sum of the remaining squares 
Q=S-U;
fprintf(' The sum of the remaining squares Q=：%d\n',Q)
% Complex determinate coefficient 
R2 = U/S;
fprintf(' Complex determinate coefficient R2=：%d\n',R2)
% Negative correlation coefficient 
R = sqrt(U/S);
fprintf(' Complex correlation coefficient R=：%d\n',R)
% Regression mean square 
% n= X_mean  The number of 
UU = U/n;
fprintf(' Regression mean square =：%d\n',UU)
% Residual mean square 
% N= Y The number of 
QQ = Q/(N-n-1);
fprintf(' Residual mean square =：%d\n',QQ)
% Residual standard deviation 
s = sqrt(QQ);
fprintf(' Residual standard deviation s=：%d\n',s)
% Equation significance test value 
F = UU/QQ;
fprintf(' Variance significance test value F=：%d\n',F)

Four 、regress Linear regression command

For univariate and multivariate linear regression , It's essentially the least squares method . stay Matlab 2014a in , Input help regress , Will pop up and regress Information about

Invocation format ：
B = regress(Y,X)
[B,BINT] = regress(Y,X)
[B,BINT,R] = regress(Y,X)
[B,BINT,R,RINT] = regress(Y,X)
B,BINT,R,RINT,STATS] = regress(Y,X)
[...] = regress(Y,X,ALPHA)

Parameter interpretation ：
B： Regression coefficient , It's a vector （“the vector B of regression coefficients in the linear model Y = X*B”）.
BINT： Interval estimates of regression coefficients （“a matrix BINT of 95% confidence intervals for B”）.
R： residual （ “a vector R of residuals”）.
RINT： confidence interval （“a matrix RINT of intervals that can be used to diagnose outliers”）.
STATS： Statistics used to test the regression model . Yes 4 A numerical ： Determination factor R^2,F Statistics Observations , Tested p Value , Estimation of error variance .
ALPHA： Significance level （ Default value if missing 0.05）.

1. Adjust the function to solve the equation

%  Equation solving function uses 
[b,bint,r,rint,stats] = regress(Y,X);

2. Plot the original and predicted values

x = 1:1:N;
plot(x,Y,'-*b',x,YY,'-or'); % linear , Color , Mark 

% hold on; % It means to continue painting on the same picture 
% title('x'); % Named title 
% axis([0 1 0 10]) %  Set the coordinate axis in the specified interval 
% xlabel('t'); % name x Axis 
% ylabel('x'); % name y Axis 
% grid on % Show axis gridlines 
% legend('Y','YY'); %* Annotate ,2 What do the lines represent *

3. Draw residual diagram ：

figure % create a window 
rcoolot(r,rint) % Draw a residual diagram

5、 ... and 、matlab color table

Linetype	explain	Marker	explain	Color	explain
-	Solid line ( Default )	+	The plus sign	r	Red
--	Double line	o	The hollow circle	g	green
:	Dotted line	*	asterisk	b	Blue
:.	Point line	.	Solid round	c	Turquoise
		x	The cross sign	m	Magenta
		s(square)	Square	y	yellow
		d	The diamond	k	black
		^	Top triangle	w	white
		v	Lower triangle
		>	Right triangle
		<	Left triangle
		p(pentagram)	Five-pointed star
		h(hexagram)	hexagon
		square	Square
		pentagram	Pentagonal
		hexagram	hexagon