当前位置:网站首页>leetcode:105. Constructing binary trees from preorder and inorder traversal sequences
leetcode:105. Constructing binary trees from preorder and inorder traversal sequences
2022-07-07 07:39:00 【uncle_ ll】
105. Construction of binary trees from traversal sequences of preorder and middle order
source : Power button (LeetCode)
link : https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
Given two arrays of integers preorder and inorder , among preorder Is the prior traversal of a binary tree , inorder Is the middle order traversal of the same tree , Please construct a binary tree and return its root node .
Example 1:
Input : preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output : [3,9,20,null,null,15,7]

Example 2:
Input : preorder = [-1], inorder = [-1]
Output : [-1]
Tips :
- 1 <= preorder.length <= 3000
- inorder.length == preorder.length
- -3000 <= preorder[i], inorder[i] <= 3000
- preorder and inorder all No repetition Elements
- inorder All appear in preorder
- preorder Guarantee It is the preorder traversal sequence of binary tree
- inorder Guarantee It is the middle order traversal sequence of binary tree
solution
- recursive : Pre order traversal and middle order traversal are given , The first element of the preorder traversal is the root node location , Then, based on the value of the root node, go to the middle order traversal to find the location of the root node , Based on this, the middle order traversal is divided into left subtree traversal and right subtree traversal results ; Find the preorder traversal of left and right subtrees in the preorder traversal based on the length of left subtree ; Next, you can recursively traverse the pre order and middle order of the left subtree , Preorder traversal and inorder traversal of right subtree ; obtain root.left And root.right, Eventually return root that will do ; The key is to find root The subscript ; If using index Way to find words , Each search requires a traversal , The complexity is O ( n ) O(n) O(n), The total complexity is O ( n 2 ) O(n^2) O(n2), Here, a hash table is used to store the subscript of the middle order traversal , Find time changed to O ( 1 ) O(1) O(1), Space for time
Code implementation
recursive
python Realization
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
n = len(preorder)
if n == 0:
return None
indexs = {
element: i for i, element in enumerate(inorder)}
def helper(preorder_left, preorder_right, inorder_left, inorder_right):
if preorder_left > preorder_right:
return None
preorder_index = preorder_left
inorder_root = indexs[preorder[preorder_index]]
root = TreeNode(preorder[preorder_index])
left_preorder_size = inorder_root - inorder_left
root.left = helper(1+preorder_left, preorder_left+left_preorder_size, inorder_left, inorder_root-1)
root.right = helper(1+preorder_left+left_preorder_size, preorder_right, inorder_root+1, inorder_right)
return root
return helper(0, n-1, 0, n-1)
c++ Realization
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */
class Solution {
private:
unordered_map<int, int> index;
public:
TreeNode* helper(const vector<int>& preorder, const vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
if (preorder_left > preorder_right)
return nullptr;
int preorder_root = preorder_left;
int inorder_root = index[preorder[preorder_root]];
TreeNode* root = new TreeNode(preorder[preorder_root]);
int size_left_subtree = inorder_root - inorder_left;
root->left = helper(preorder, inorder, preorder_left+1, preorder_left+size_left_subtree, inorder_left, inorder_root-1);
root->right = helper(preorder, inorder, preorder_left+size_left_subtree+1, preorder_right, inorder_root+1, inorder_right);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n = preorder.size();
if (n == 0)
return nullptr;
for (int i=0; i<n; i++) {
index[inorder[i]] = i;
}
return helper(preorder, inorder, 0, n-1, 0, n-1);
}
};
Complexity analysis
- Time complexity : O ( N ) O(N) O(N)
- Spatial complexity : O ( N ) O(N) O(N)
边栏推荐
猜你喜欢

抽絲剝繭C語言(高階)數據的儲存+練習

Project practice five fitting straight lines to obtain the center line

Tencent's one-day life
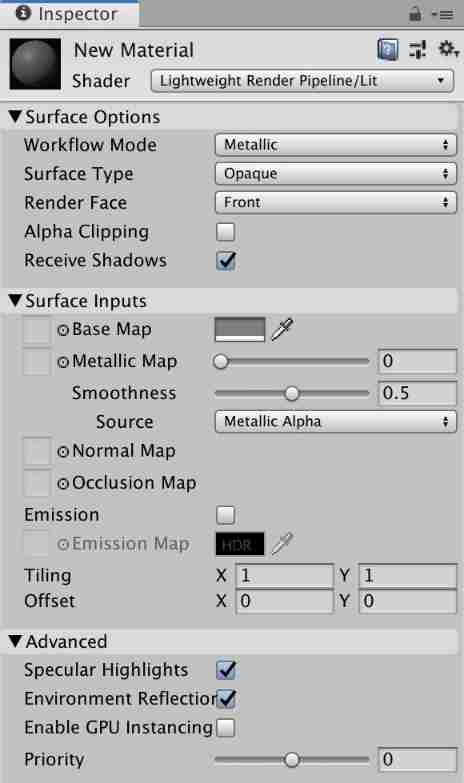
URP - shaders and materials - light shader lit
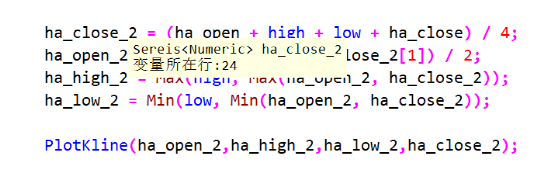
Lm11 reconstruction of K-line and construction of timing trading strategy
Bi she - college student part-time platform system based on SSM

Music | cat and mouse -- classic not only plot

Deep learning Flower Book + machine learning watermelon book electronic version I found

L'externalisation a duré trois ans.
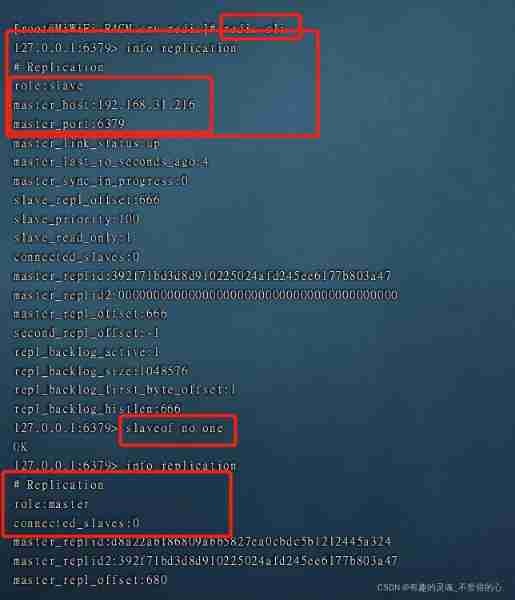
Redis data migration
随机推荐
vus. Precautions for SSR requesting data in asyndata function
Advanced level of C language (high level) pointer
IO流 file
KBU1510-ASEMI电源专用15A整流桥KBU1510
Hidden Markov model (HMM) learning notes
海思芯片(hi3516dv300)uboot镜像生成过程详解
The annual salary of general test is 15W, and the annual salary of test and development is 30w+. What is the difference between the two?
3、 High quality programming and performance tuning practical youth training camp notes
I failed in the postgraduate entrance examination and couldn't get into the big factory. I feel like it's over
深度学习花书+机器学习西瓜书电子版我找到了
After 95, Alibaba P7 published the payroll: it's really fragrant to make up this
普通测试年薪15w,测试开发年薪30w+,二者差距在哪?
毕设-基于SSM大学生兼职平台系统
Differences between H5 architecture and native architecture
Determining the full type of a variable
Leetcode-226. Invert Binary Tree
MySQL service is missing from computer service
Bindingexception exception (error reporting) processing
After 95, the CV engineer posted the payroll and made up this. It's really fragrant
按键精灵脚本学习-关于天猫抢红包