当前位置:网站首页>OFDM Lecture 16 5 -Discrete Convolution, ISI and ICI on DMT/OFDM Systems
OFDM Lecture 16 5 -Discrete Convolution, ISI and ICI on DMT/OFDM Systems
2022-08-05 05:12:00 【Ming Dynasty Bai Xiaosheng】
参考:

The point of this article is very fresh and intuitive,Mainly from the linear algebra to explain the relevant principles
目录:
1: 离散卷积
2: ISI & ICI
一 离散卷积
The convolution formula for continuous data was discussed earlier

In fact, there is no continuous data, we generally use discrete convolution,
![y(k)=\sum_{0}^{\infty} x[n] \bullet h[k-n]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_21.gif)
假设x的长度为n, h的长度为m, y的长度为n+m
1.1 例子
假设
![x=[x_0,x_1,x_2,x_3]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_19.gif)
![h=[h_0,h_1,h_2,h_3]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_15.gif)
![y_0=\sum_{n=0}^{3}x[n]\bullet h[0-n]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_0.gif)

![y_1=\sum_{n=0}^{3}x[n]\bullet h[1-n]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_6.gif)

![y_2=\sum_{n=0}^{3}x[n]\bullet h[2-n]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_23.gif)

![y_3=\sum_{n=0}^{3}x[n]\bullet h[3-n]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_28.gif)

It's essentially the multiplication of two matrices
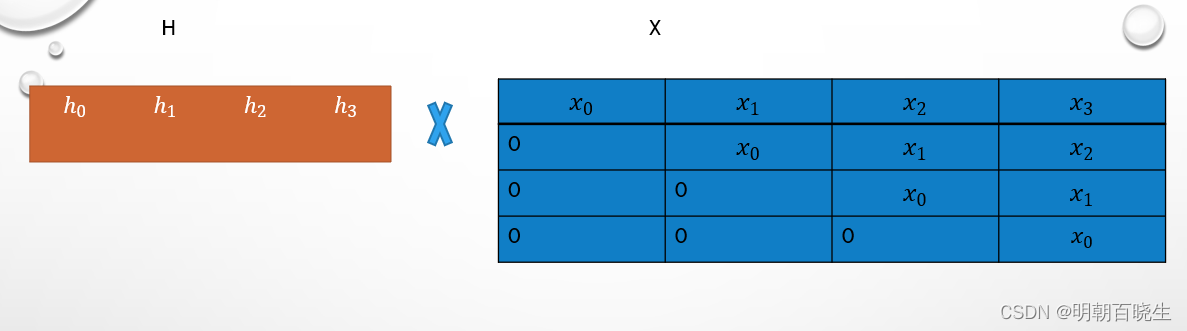
Further representation method,如下图,Multiply and sum the corresponding column elements

二 CP(Cyclic prefix) CS(Cyclic suffix)
2.1 循环前缀,Cyclic suffix structure

发送端
经过IDFT After inverse discrete Fourier transform,得到长度为Ntime domain data
Then insert a length of a 的cp, 以及长度为b 的 cs

假设原始数据为
![X=[x_0,x_1,x_2,x_3]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_18.gif)
a= b=2
![cp=[x_2,x_3], cs=[x_0,x_1]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_8.gif)
Finally the data becomes

2.2 ICI
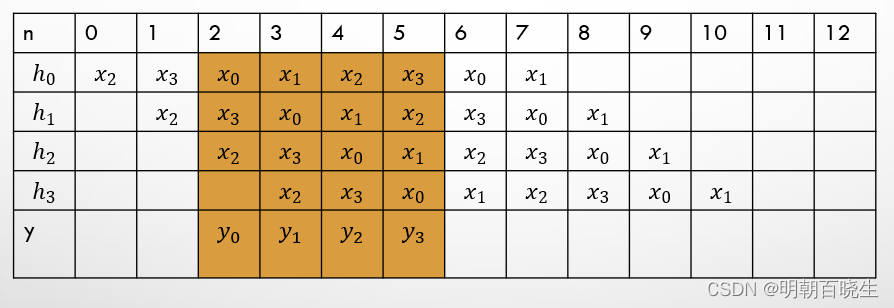
when decoding,We will Fourier transform it,对CP,CS 部分丢弃

如下

One more noise was found 

 ,interference between other channels
,interference between other channels
下面是草图

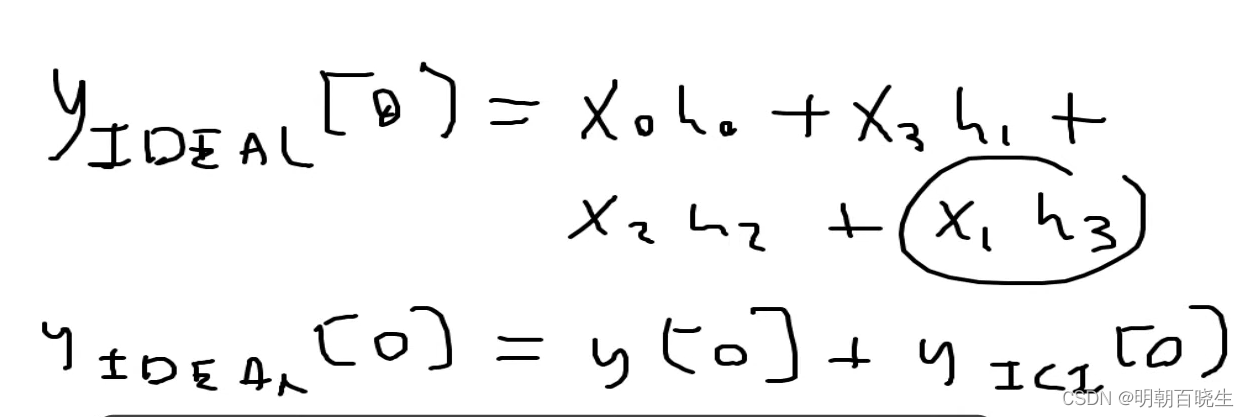
2.3 ISI 模型
跟上面差不多

,
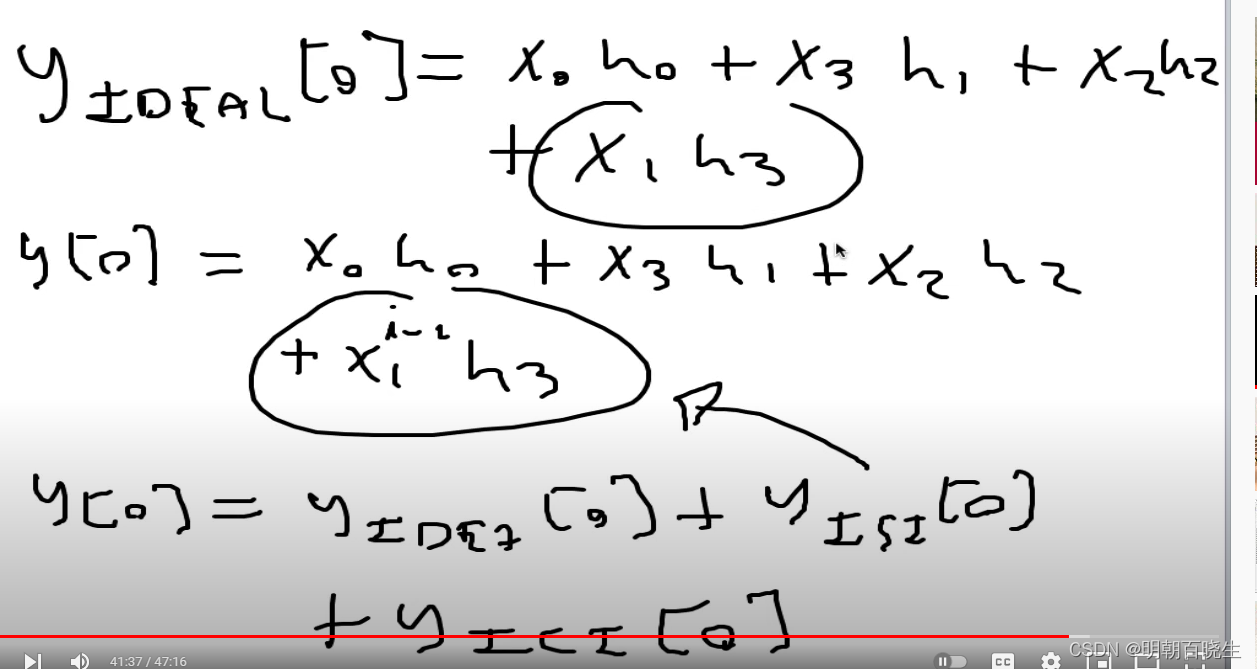
边栏推荐
- write the story about us
- 请写出SparkSQL语句
- LAB 信号量实现细节
- Redis - 13、开发规范
- 【无标题】
- Community Sharing|Tencent Overseas Games builds game security operation capabilities based on JumpServer
- 2022牛客多校第四场C.Easy Counting Problem(EGF+NTT)
- OFDM 十六讲 5 -Discrete Convolution, ISI and ICI on DMT/OFDM Systems
- [Surveying] Quick Summary - Excerpt from Gaoshu Gang
- server disk array
猜你喜欢
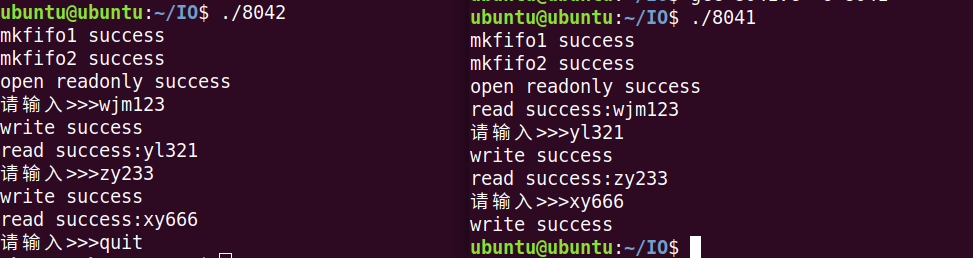
Homework 8.4 Interprocess Communication Pipes and Signals
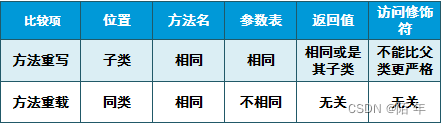
Day019 Method overriding and introduction of related classes

shell函数
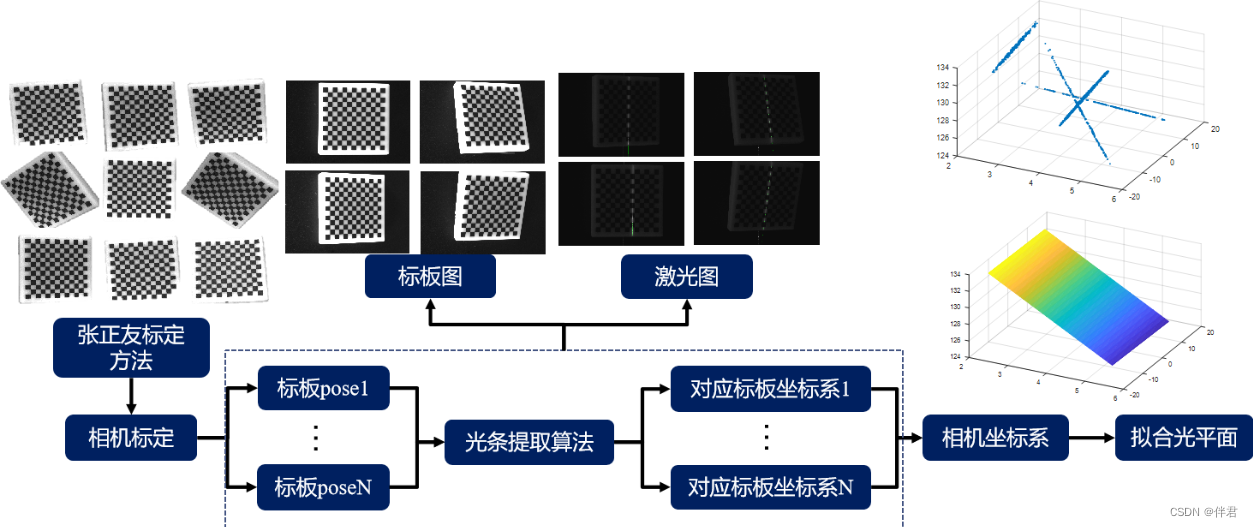
结构光三维重建(二)线结构光三维重建

雷克萨斯lm的安全性到底体现在哪里?一起来看看吧

The difference between span tag and p
Mini Program_Dynamic setting of tabBar theme skin

Reverse theory knowledge 4
![[cesium] 3D Tileset model is loaded and associated with the model tree](/img/03/50b7394f33118c9ca1fbf31b737b1a.png)
[cesium] 3D Tileset model is loaded and associated with the model tree

Basic properties of binary tree + oj problem analysis
随机推荐
开发一套高容错分布式系统
How does the Flutter TapGestureRecognizer work
2023年信息与通信工程国际会议(JCICE 2023)
结构光三维重建(二)线结构光三维重建
人性的弱点
C语言-大白话理解原码,反码和补码
数字孪生技术在电力系统中的应用现状
Day14 jenkins deployment
结构光三维重建(一)条纹结构光三维重建
作业8.4 进程间的通信 管道与信号
多线程查询结果,添加List集合
dedecms error The each() function is deprecated
uboot开启调试打印信息
入口点注入
Redis - 13、开发规范
The role of DataContext in WPF
u-boot debugging and positioning means
After controlling the export file in MySQL, it becomes \N. Is there any solution?
Qt produces 18 frames of Cupid to express his love, is it your Cupid!!!
Please write the SparkSQL statement