当前位置:网站首页>2022/7/1學習總結
2022/7/1學習總結
2022-07-05 04:57:00 【ls真的不會啊】
一、102. 二叉樹的層序遍曆 - 力扣(LeetCode)
題目描述
給你二叉樹的根節點 root ,返回其節點值的 層序遍曆 。 (即逐層地,從左到右訪問所有節點)。
示例 1:
輸入:root = [3,9,20,null,null,15,7]
輸出:[[3],[9,20],[15,7]]
示例 2:輸入:root = [1]
輸出:[[1]]
示例 3:輸入:root = []
輸出:[]
提示:
樹中節點數目在範圍 [0, 2000] 內
-1000 <= Node.val <= 1000
思路
層序遍曆過程,其實就是從上到下,從左到右依次將每個數放入到隊列中,然後按順序依次打印就是想要的結果。
代碼實現
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> a;
queue<TreeNode*> q;
if(root!=NULL)//根結點
{
q.push(root);
}
while(!q.empty())
{
vector<int> b;
int size=q.size();
while(size--)
{
//遍曆完該結點的左右子結點的時候,就將該結點出隊列
if(q.front()->left)
{
q.push(q.front()->left);
}
if(q.front()->right)
{
q.push(q.front()->right);
}
b.push_back(q.front()->val);
q.pop();
}
a.push_back(b);
}
return a;
}
};二、20. 有效的括號 - 力扣(LeetCode)
題目描述
給定一個只包括 '(',')','{','}','[',']' 的字符串 s ,判斷字符串是否有效。
有效字符串需滿足:
左括號必須用相同類型的右括號閉合。
左括號必須以正確的順序閉合。
示例 1:
輸入:s = "()"
輸出:true
示例 2:輸入:s = "()[]{}"
輸出:true
示例 3:輸入:s = "(]"
輸出:false
示例 4:輸入:s = "([)]"
輸出:false
示例 5:輸入:s = "{[]}"
輸出:true
提示:
1 <= s.length <= 104
s 僅由括號 '()[]{}' 組成
思路
這就是一個簡單的關於棧的題目。如果遇到左半邊括號,就入棧。如果遇到右半邊括號,就拿棧頂元素和它比較,如果兩者匹配的話,就出棧,否則,字符串無效。如果前面這一步沒有出問題,就最後檢查一下棧是否為空,如果非空,那字符串無效。
代碼實現
class Solution {
public:
bool isValid(string s) {
char a[10001];
int top=0;
for(int i=0;i<s.length();i++)
{
if(s[i]=='('||s[i]=='['||s[i]=='{')
{
a[top++]=s[i];
}
else
{
if(s[i]==')')
{
if(top>0&&a[top-1]=='(')
{
top--;
}
else
{
return false;
}
}
if(s[i]=='}')
{
if(top>0&&a[top-1]=='{')
{
top--;
}
else
{
return false;
}
}
if(s[i]==']')
{
if(top>0&&a[top-1]=='[')
{
top--;
}
else
{
return false;
}
}
}
}
if(top==0)
{
return true;
}
else
{
return false;
}
}
};三、121. 買賣股票的最佳時機 - 力扣(LeetCode)
題目描述
給定一個數組 prices ,它的第 i 個元素 prices[i] 錶示一支給定股票第 i 天的價格。
你只能選擇 某一天 買入這只股票,並選擇在 未來的某一個不同的日子 賣出該股票。設計一個算法來計算你所能獲取的最大利潤。
返回你可以從這筆交易中獲取的最大利潤。如果你不能獲取任何利潤,返回 0 。
示例 1:
輸入:[7,1,5,3,6,4]
輸出:5
解釋:在第 2 天(股票價格 = 1)的時候買入,在第 5 天(股票價格 = 6)的時候賣出,最大利潤 = 6-1 = 5 。
注意利潤不能是 7-1 = 6, 因為賣出價格需要大於買入價格;同時,你不能在買入前賣出股票。
示例 2:輸入:prices = [7,6,4,3,1]
輸出:0
解釋:在這種情况下, 沒有交易完成, 所以最大利潤為 0。
提示:
1 <= prices.length <= 105
0 <= prices[i] <= 104
思路
因為如果沒有合適的價格,則不進行交易,利潤為0,所以以賣出日期為准,找賣出日期之前的最小買入價格,從而找到每個賣出日期能獲得的最大利潤。
代碼實現
class Solution {
public:
int maxProfit(vector<int>& prices) {
int max,min=prices[0],dp[prices.size()];
dp[0]=0;
max=dp[0];
for(int i=1;i<prices.size();i++)
{
if(prices[i]<min)//該日之前的最小的買入價格
{
min=prices[i];
}
dp[i]=prices[i]-min;
if(max<dp[i])
{
max=dp[i];
}
}
return max;
}
};边栏推荐
- MySQL audit log Archive
- 中国针状焦行业发展研究与投资价值报告(2022版)
- Rip notes [rip message security authentication, increase of rip interface measurement]
- 54. Spiral matrix & 59 Spiral matrix II ●●
- Flutter tips: various fancy nesting of listview and pageview
- The difference between heap and stack
- django连接数据库报错,这是什么原因
- 中国聚氨酯硬泡市场调研与投资预测报告(2022版)
- Personal required code
- AutoCAD - Zoom previous
猜你喜欢
![[groovy] closure (closure parameter binding | curry function | rcurry function | ncurry function | code example)](/img/90/0cf08ae6fea61891e3e1fdf29d310c.jpg)
[groovy] closure (closure parameter binding | curry function | rcurry function | ncurry function | code example)
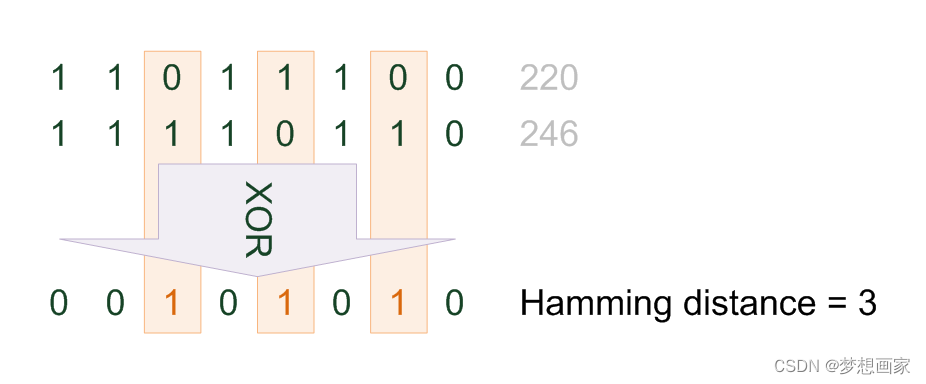
Introduce Hamming distance and calculation examples
3dsmax scanning function point connection drawing connection line
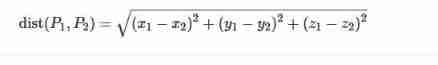
【acwing】528. cheese
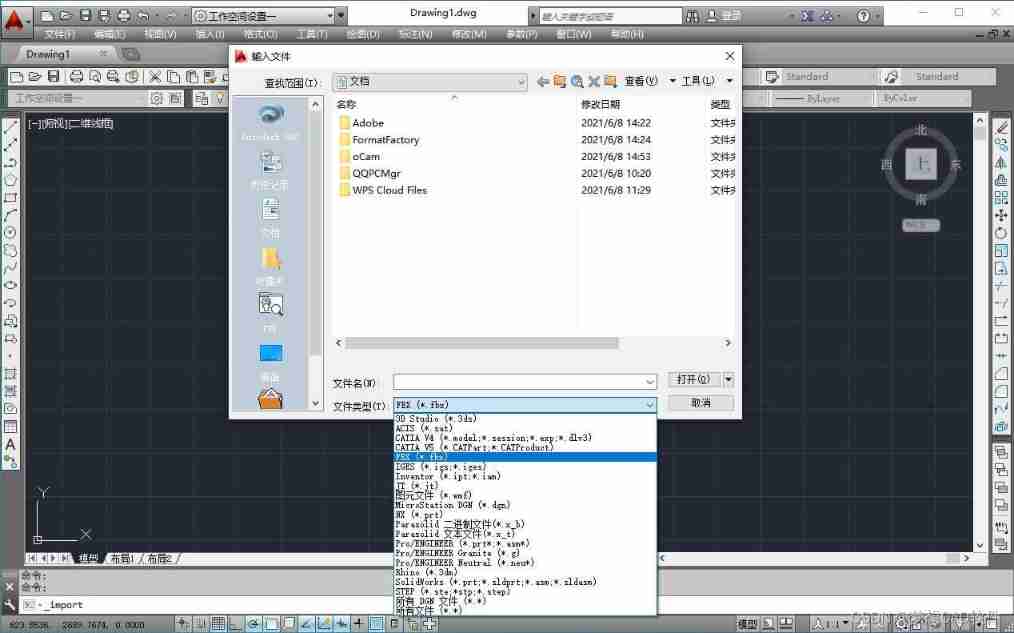
AutoCAD - graphic input and output

JVM 原理和流程简介

Redis 排查大 key 的4种方法,优化必备

UE4/UE5 虚幻引擎,材质篇(三),不同距离的材质优化

Special information | real estate and office buildings - 22.1.9
![[groovy] closure (closure parameter list rule | default parameter list | do not receive parameters | receive custom parameters)](/img/36/c4206a95c007e41df628d99e06ba18.jpg)
[groovy] closure (closure parameter list rule | default parameter list | do not receive parameters | receive custom parameters)
随机推荐
Fluent objects and lists
AutoCAD - workspace settings
Thematic information | carbon, carbon neutrality, low carbon, carbon emissions - 22.1.9
【acwing】528. cheese
Unity enables mobile phone vibration
Cocos create Jiugongge pictures
Redis 排查大 key 的4种方法,优化必备
AutoCAD - set layer
Unity synergy
数论函数及其求和 待更新
AutoCAD - graphic input and output
中国溶聚丁苯橡胶(SSBR)行业研究与预测报告(2022版)
AutoCAD - full screen display
中国聚氨酯硬泡市场调研与投资预测报告(2022版)
Research and forecast report on China's solution polymerized styrene butadiene rubber (SSBR) industry (2022 Edition)
Thinking of 2022 American College Students' mathematical modeling competition
Séparation et combinaison de la construction du système qualité
Establish cloth effect in 10 seconds
Use assimp library to read MTL file data
质量体系建设之路的分分合合