数论函数及其求和 待更新

主要记录一下相关的题目，略过知识讲解。

例题1 数论分块

P3935 Calculating

题目描述

若 $x$ 分解质因数结果为 $x=p_1^{k_1}{p}_2^{k_2}\cdots p_n^{k_n}$，令$f(x)=(k_1+1)(k_2+1)\cdots (k_n+1)$，求 ${\sum }_{i=l}^{r}f(i)$ 对 $998244353$ 取模的结果。
时间复杂度 $O(\sqrt{n})$。

思路

首先要知道 $f(x)$ 其实就是 $x$ 的约数个数。（每种素因子都有 $k_i$ 个那么可以取 $0,1,...,k_i$ 一共 $k_i+1$ 种取法排列组合，由唯一分解定理显然乘积都是不同的）因为题目要求的是区间和，于是正常地转化为前缀和形式 $ans={\sum }_{i=1}^{r}f(x)-{\sum }_{i=1}^{l-1}f(x)$ ，设 $S(n)={\sum }_{i=1}^{n}f(x)$，问题转化为了求 $S(n)$ ，也就是求 $1-n$ 这 $n$ 个数的因数个数之和。

$1-n$ 中含有因子 $i$ 的数一共有 $\lfloor \frac{n}{i}\rfloor$ ，直接用数论分块即可。

代码

int ll, rr, n;
int cal(int l, int r) {
    
	int ansr = 0, ansl = 0;
	n = rr;
    for(int l=1,r;l<=n;l=r+1){
    
        r=n/(n/l);
        ansr+=(n/l)*(r-l+1) % P;	
        ansr %= P;
    }
    n = ll;
    for(int l=1,r;l<=n;l=r+1){
    
        r=n/(n/l);
        ansl+=(n/l)*(r-l+1) % P;	
        ansl %= P;
    }
    ansr = (ansr - ansl + P) % P;
    return ansr;
}
void solve() {
    
    cin >> ll >> rr;
    ll--;
    cout << cal(ll, rr) << endl;
}

例题2 数论分块

P2303 [SDOI2012] Longge 的问题

题目描述

给定一个整数 $n$，你需要求出 $\sum _{i=1}^n\gcd (i,n)$，$n<10^9$

思路

注意到 $gcd(i,n)$ 的取值最多只有 $n$ 的约数个，所以考虑按取值分类，而且出现 $gcd$ 的题往往都需要想办法凑出 $gcd(i,j)=1$，于是我们把原式化为 $$\sum _{d|n}d\sum _{i=1}^n[gcd(i,n)=d]=\sum _{d|n}d\sum _{i=1}^{\frac{n}{d}}[gcd(i,\frac{n}{d})=1]=\sum _{d|n}d\varphi (\frac{n}{d})$$
可以通过枚举 $n$ 的约数直接求，时间复杂度 $O(\sqrt{n})$。

代码

void solve() {
    
    cin >> n;
    ll ans = 0;
    for(ll i = 1; i * i <= n; i++) {
    
    	if(n % i == 0) {
    
	    	ans += i * phi(n/i);
	    	if(n/i!=i) {
    
	    		ans += (n/i) * phi(i);
	    	}
    	}
    }
    cout << ans << endl;
}

莫比乌斯函数

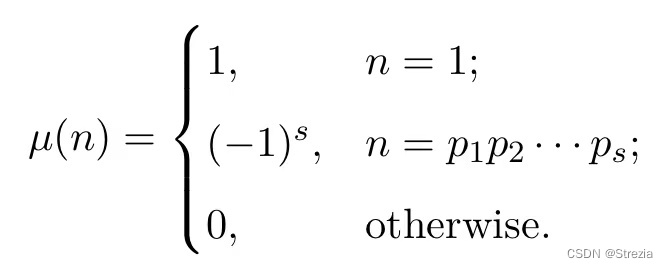
常用卷积

$ϵ=\mu \ast 1,Id=\varphi \ast 1$ 。
即 $ϵ(n)={\sum }_{d|n}\mu (d)$ 。其中 $ϵ(n)=1$ 当且仅当 $n=1$，否则 $=0$ 。

引例

给定 $n,m$，求二元组 $(x,y)$ 的个数，满足 $1\le x\le n$ ， $1\le y\le m$ ，且 $gcd(x,y)=1$ 。$n,m\le 10^7$ ，至多 $10^4$ 组数据。

思路

$$\sum _{x=1}^n\sum _{y=1}^m[gcd(x,y)=1]=\sum _{x=1}^n\sum _{y=1}^mϵ(gcd(x,y))=\sum _{x=1}^n\sum _{y=1}^m\sum _{d|gcd(x,y)}\mu (d)$$
$$=\sum _{x=1}^n\sum _{y=1}^m\sum _{d|x,d|y}\mu (d)==\sum _{d=1}^{min(n,m)}\mu (d)\lfloor \frac{n}{d}\rfloor \lfloor \frac{m}{d}\rfloor$$
对上式预处理 $\mu$ 及其前缀和，按 $\lfloor \frac{n}{d}\rfloor \lfloor \frac{m}{d}\rfloor$ 的取值分段，就可以每组询问 $O(\sqrt{n})$ 解决问题。

例题3 莫比乌斯反演

[SDOI2015]约数个数和

题目描述

设 $d(x)$ 为 $x$ 的约数个数，给定 $n,m$，求
$$\sum _{i=1}^n\sum _{j=1}^{m}d(ij)$$
【数据范围】
对于 $100\%$ 的数据，$1\le T,n,m\le 50000$。

思路

首先有结论：
$$d(ij)=\sum _{x|i}\sum _{y|j}[gcd(x,y)=1]$$

则原式：
$$\sum _{i=1}^n\sum _{j=1}^{m}d(ij)=\sum _{i=1}^n\sum _{j=1}^m\sum _{x|i}\sum _{y|j}[gcd(x,y)=1]=\sum _{x=1}^n\sum _{y=1}^m[gcd(x,y)=1]\lfloor \frac{n}{x}\rfloor \lfloor \frac{m}{y}\rfloor$$
将引例中结论带入：
$$=\sum _{d=1}^{min(n,m)}\mu (d)\sum _{x=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{y=1}^{\lfloor \frac{m}{d}\rfloor }\lfloor \frac{n}{xd}\rfloor \lfloor \frac{m}{yd}\rfloor =\sum _{d=1}^{min(n,m)}\mu (d)\sum _{x=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{y=1}^{\lfloor \frac{m}{d}\rfloor }\lfloor \frac{\lfloor \frac{n}{d}\rfloor }{x}\rfloor \lfloor \frac{\lfloor \frac{m}{d}\rfloor }{y}\rfloor$$
令 $f(n)={\sum }_{i=1}^n\lfloor \frac{n}{i}\rfloor$ ，则
$$=\sum _{d=1}^{min(n,m)}\mu (d)f(\lfloor \frac{n}{d}\rfloor )f(\lfloor \frac{m}{d}\rfloor )$$
又 $f(n)={\sum }_{i=1}^n\lfloor \frac{n}{i}\rfloor ={\sum }_{k=1}^{n}d(k)$
故可以通过欧拉筛 $O(n)$ 预处理出 $d(n)$，通过前缀和得到 $f(n)$，可以每次询问 $O(\sqrt{n})$ 回答。

代码

int mu[maxn], prim[maxn], sum[maxn], cnt;
int g[maxn];
bool vis[maxn];
void get_mu(int n)
{
    
    mu[1]=1;
    for(int i=2;i<=n;i++)
    {
    
        if(!vis[i]){
    prim[++cnt]=i;mu[i]=-1;}
        for(int j=1;j<=cnt&&prim[j]*i<=n;j++)
        {
    
            vis[prim[j]*i]=1;
            if(i%prim[j]==0)break;
            else mu[i*prim[j]]=-mu[i];
        }
    }
    for(int i=1;i<=n;i++)sum[i]=sum[i-1]+mu[i];
    for(int i=1;i<=n;i++)
    {
    
        long long ans=0;
        for(int l=1,r;l<=i;l=r+1)
        {
    
            r=(i/(i/l));
            ans+=1ll*(r-l+1)*1ll*(i/l);
        }
        g[i]=ans;
    }
}
void solve() {
    
    int n, m;
    cin >> n >> m;
    int ans = 0;
    int mn = min(n, m);
    for(int l = 1, r; l <= mn; l = r + 1){
    
    	r = min(n/(n/l), m/(m/l));
        ans += (sum[r] - sum[l-1]) * g[n/l] * g[m/l];
    }
    cout << ans << endl;
}