LIS longest ascending subsequence problem (dynamic programming, greed + dichotomy)

Refer to the problem-solving method learned in a boss blog ：LIS（ Longest ascending subsequence ） Three ways to solve the problem and some examples

Longest ascending subsequence

First, understand two concepts ：

1. Substring

A subsequence of any consecutive characters in a string is called a substring of the string

For a string variable , for example "abcde", Its substring is like "abc" In this way, you can find the continuous string . character string "abcde" It also belongs to its longest substring .

Calculation of the number of substrings ：
abc The string of ：a、 b、 c、 ab、 bc 、abc、/0 common （3+2+1+1） individual ,
if The length of the string is n, be The number of substrings is [n*(n+1)/2+1] individual , for example ："software" The number of neutron strings is 8+7+…+1+1=37 individual , That is to say 37 individual .
Special ！ For substrings that have the same continuity ( for example :AAABBBCCC) The calculation method of such a substring yes n(n+1)/2+1- Repeat substring
 

2. Subsequence

Subsequence is to find a part of the original sequence , Not necessarily continuous, but the sequence is consistent with the original sequence

Such as “abcdefg” in ,acd,bdf Its subsequence , and bac,dbfg It is not , Because they are inconsistent with the character order of the string .
 
difference ：
Longest common subsequence （LCS） It's one in a sequence set （ It's usually two sequences ） The problem of finding the longest subsequence in all sequences . The difference between this and the problem of finding the longest common substring is ： Subsequences do not need to occupy continuous positions in the original sequence ; And the longest common subsequence must be continuous .
 
 

LIC Definition

Longest ascending subsequence （Longest Increasing Subsequence）, abbreviation LIS, It's one in a sequence set （ It's usually two sequences ） The problem of finding the longest subsequence in all sequences . In some cases, the longest non descending subsequence , The difference between the two is whether there can be equal numbers in the sequence .
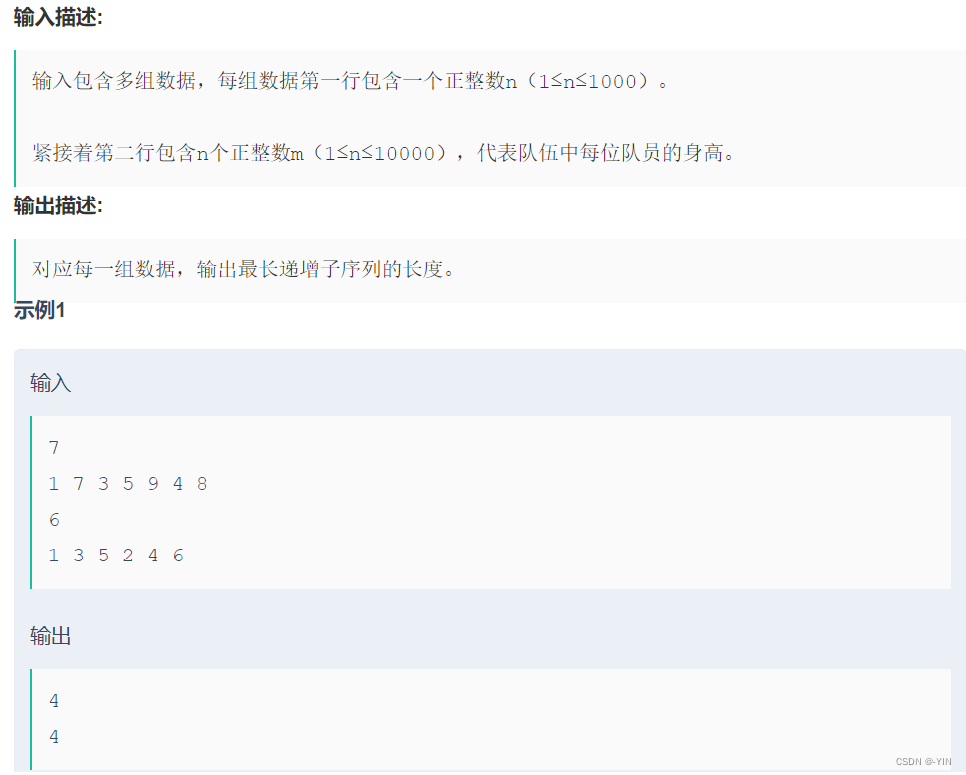
Suppose we have a sequence b i, When b1 < b2 < … < bn When , We call this sequence ascending . For a given sequence (a1, a2, …, aN), We can also get some ascending subsequences (ai1, ai2, …, aiK), here 1 <= i1 < i2 < … < iK <= N, But it must be in the order from front to back . such as , For the sequence (1, 7, 3, 5, 9, 4, 8), We'll get some ascending subsequences , Such as (1, 7, 9), (3, 4, 8), (1, 3, 5, 8) wait , And the longest of these subsequences （ Such as subsequence (1, 3, 5, 8) ）, Its length is 4, Therefore, the length of the longest ascending subsequence of the sequence is 4.

If you just look at the definition, you will find it difficult to understand , So let's look at an example first

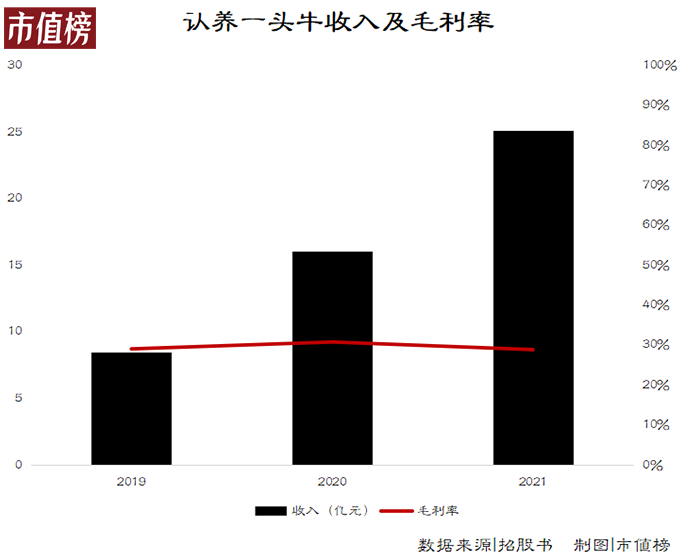
Example ： Square dance team

Topic link ：
source ： Cattle from
There is a team standing in the square , They are Yangko teams from all over the country , Now we have their height data , Please help find out the subsequence of increasing height . For example, the height data of the team is （1、7、3、5、9、4、8）, Among them, the increasing subsequences are （1、7）,（1、3、5、9）,（1、3、4、8） etc. , The longest length is 4.

analysis ： For fixed arrays , although LIS Sequence is not necessarily unique , but LIS The length of is unique .
From the example given in the title

Dynamic programming

Time complexity O(n²), Spatial complexity O(n)

Give a value equal to the length of the sequence dp Array , Subscript i Express With arr[ i ] At the end of the LIS The length of

State transition equation ：dp[i] = max( dp[i],dp[j] + 1)

d(i) Is to find A[ i ] The longest subsequence at the end , stay A[ i ] The longest ascending subsequence before +1, The former i The number of LIS length + 1. When A[ i ] There's nothing like A[ i ] Smaller numbers ,d(i) = 1. be-all d(i) The largest one is the longest ascending subsequence .
In fact, it's more popular , Namely Each time, look forward to the position of the smaller number and the larger number , Replace the first one larger than it , Although this operation LIS The specific number of the sequence may change , But obviously LIS The length remains the same

#include <iostream>
#include <vector>
using namespace std;

//  Dynamic programming 
size_t MostAddSub(vector<int>& v){
    
    vector<int> dp(v.size(), 1);
    size_t sum = 1;
    for(size_t i = 0; i < v.size(); ++i){
    
        for(size_t j = 0; j < i; ++j){
    
            if(v[i] > v[j])
                dp[i] = dp[i] > dp[j]+1 ? dp[i] : dp[j]+1;
        }
        sum = sum > dp[i] ? sum : dp[i];
    }
    return sum;
}

int main()
{
    
	int n;
	while (cin >> n){
    
		vector<int> v(n);
		for (int i = 0; i < n; ++i)
			cin >> v[i];
        cout << MostAddSub(v) << endl;
    }
	return 0;
}

 
 

greedy + Dichotomy

Time complexity O(nlogn), Spatial complexity O(n)

The explanation in the boss' article

Give a new one low Array ,low [ i ] The length is i Of LIS The smallest value at the end of the element . For a ascending subsequence , Obviously, the smaller the ending element , The more advantageous it is to be followed by other elements , The more likely it is to become longer . therefore , We just need to maintain low Array , For each of these a[ i ], If a[ i ] > low [ The longest at present LIS length ], Just put a [ i ] Receive the longest LIS Back , namely low [++ The longest at present LIS length ] = a [ i ].
 
For each of these a [ i ], If a [ i ] Can receive LIS Back , Just connect it ; otherwise , Just use a [ i ] Get updates low Array . The way to do it is , stay low Array Two points search find The first is greater than or equal to a [ i ] The elements of low [ j ], use a [ i ] To update low [ j ]. If you scan it from beginning to end low Array words , The time complexity is still O(n^2). We noticed that low The interior of the array must be monotonous , So we can split low Array , Find the first one greater than or equal to a[ i ] The elements of . Once in two low The time complexity of the array O(lgn), So the total time complexity is zero O(nlogn).

Have to say , Where there are two points, the boundary of two points is always the most disgusting and difficult , The overall thinking is not difficult .

1. Create a new length of n+1 Array of low , Array low[i] The length is i The minimum value of the end element of the longest ascending subsequence of .

It's an array 1,2,3,4,5,6 The middle length is 3 The ascending subsequence of can be 1,2,3 It can also be for 2,3,4 wait , however d[3]=3, That is, the minimum element at the end of the subsequence is 3（1,2,3）

2. low Arrays are monotonic , That is to say ：（1） You can use dichotomy ;（2） Array low The length of is the length of the longest subsequence ;

We then need to prove the array low Monotonicity , To prove i<j when ,low [i]<low [j], Use counter evidence , Suppose there is k<j when ,low [k]>low [j], But when the length is j, The last element is low [j] The subsequence A in , Will later j-i Subtract elements , You can get a length of i The subsequence B, Its last element t1 Must be less than low [j]（ Because in subsequence A in ,t1 The position of is d[j] Behind ）, And let's assume an array low Must conform to the length of i The minimum value of the end element of the longest ascending subsequence of , In this case, the length is i The last element of a subsequence of t1 < low [j] < low [k], namely t1<low [k], therefore low [k] It's not the smallest , Conflict with the design , Therefore, its monotonicity can be proved

//  Two points search v First of all >=num The element subscript of 
size_t Binary_search(vector<int>& low, int right, int num){
    
	int left = 1, mid;
	while (left <= right){
    
		mid = ((right-left)>>1)+left;
		if (low[mid] < num)
            left = mid + 1;
		else
			right = mid - 1;
	}
	return left;
}
//  Calculate the maximum ascending subsequence length 
size_t FIS(vector<int>& v){
    
    vector<int> low(v.size()+1, 0);
    size_t retLen = 1;
    low[retLen] = v[0];
    for(size_t i = 1; i < v.size(); ++i){
    
        if(low[retLen] < v[i])
            low[++retLen] = v[i];
        else
            low[Binary_search(low, retLen, v[i])] = v[i];// Two points search 
    }
    return retLen;
}

Use binary search interface ：
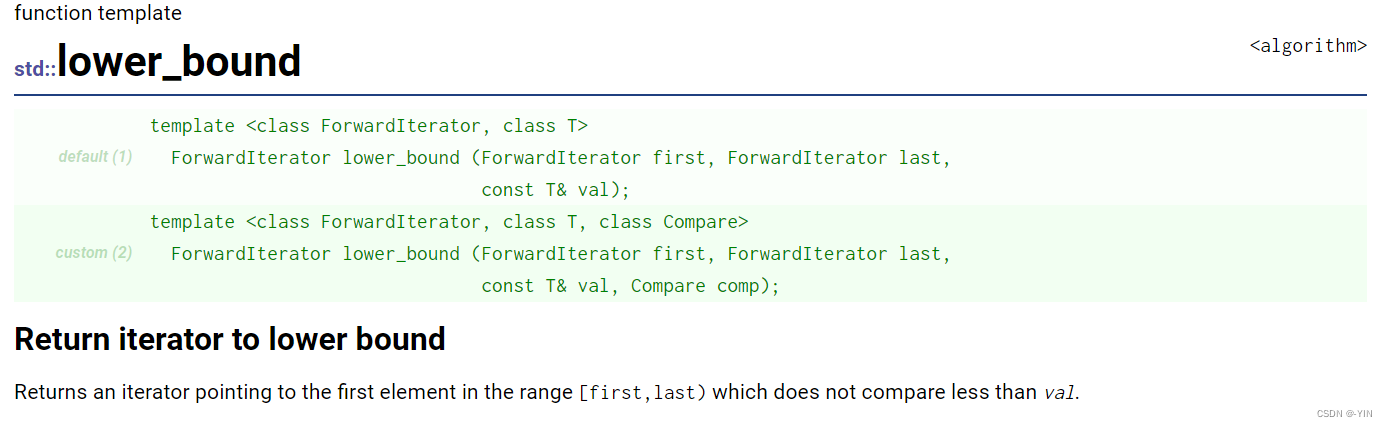
Or you can use STL In the library <algorithm> The binary lookup value location provided in (lower_bound()) Methods

STL There are three functions about binary search in lower_bound 、upper_bound 、binary_search . These three functions are applied to ordered intervals （ Of course, this is also the premise of using binary search ）.
If you are looking for val There is , that lower_bound Returns an iterator pointing to the first of these elements .upper_bound Returns an iterator pointing to the next position of the last element （ To be clear, return without breaking the order , Pluggable value Last position of ）. If you're looking for value non-existent , that lower_bound and upper_bound All back to “ Assuming that such elements exist, where they should appear ”.
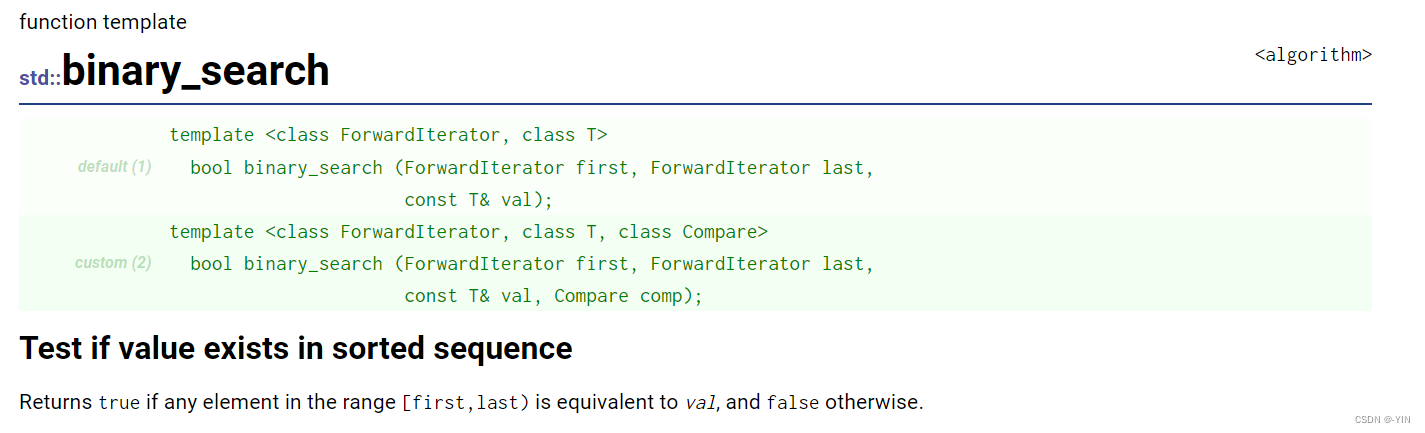
binary_search An attempt has been made to sort [first,last) Looking for elements val, If it exists, return true, If not, return false. Returning simple Boolean values may not meet the requirements , and lower_bound、upper_bound Can provide additional information . In fact, it can be seen from the source code binary_search Is to make use of lower_bound Find out where the element should appear , Then compare the position The value of is equal to value Value . There are two versions of this function. One is operator< , The other is to use the imitative function comp Compare .

binary_search This method is to judge val Whether in the sequence , The return is bool value , This question can't be used

See ：STL Two points search ——lower_bound 、upper_bound 、binary_search

    int lengthOfLIS(vector<int>& nums) {
    
        vector<int> low;
        low.push_back(nums[0]);
        for(int i = 1; i < nums.size(); ++i){
    
            if(low.back() < nums[i])
                low.push_back(nums[i]);
            else{
    
                // lower_bound  Returns the iterator that found the location 
                *(lower_bound(low.begin(), low.end(), nums[i]))=nums[i];
            }
        }
        return low.size();
    }