当前位置:网站首页>I-BERT
I-BERT
2022-07-06 08:51:00 【cyz0202】
背景
本文介绍ICML2021 I-BERT: Integer-only BERT Quantization
文章目的是对BERT进行更彻底的量化和整型计算;
作者认为之前的量化方案没有对gelu、softmax这些非线性操作进行量化计算(如下图1),即保持了float类型的计算,不仅影响计算效率,而且不能部署到某些只支持整型计算的芯片上;
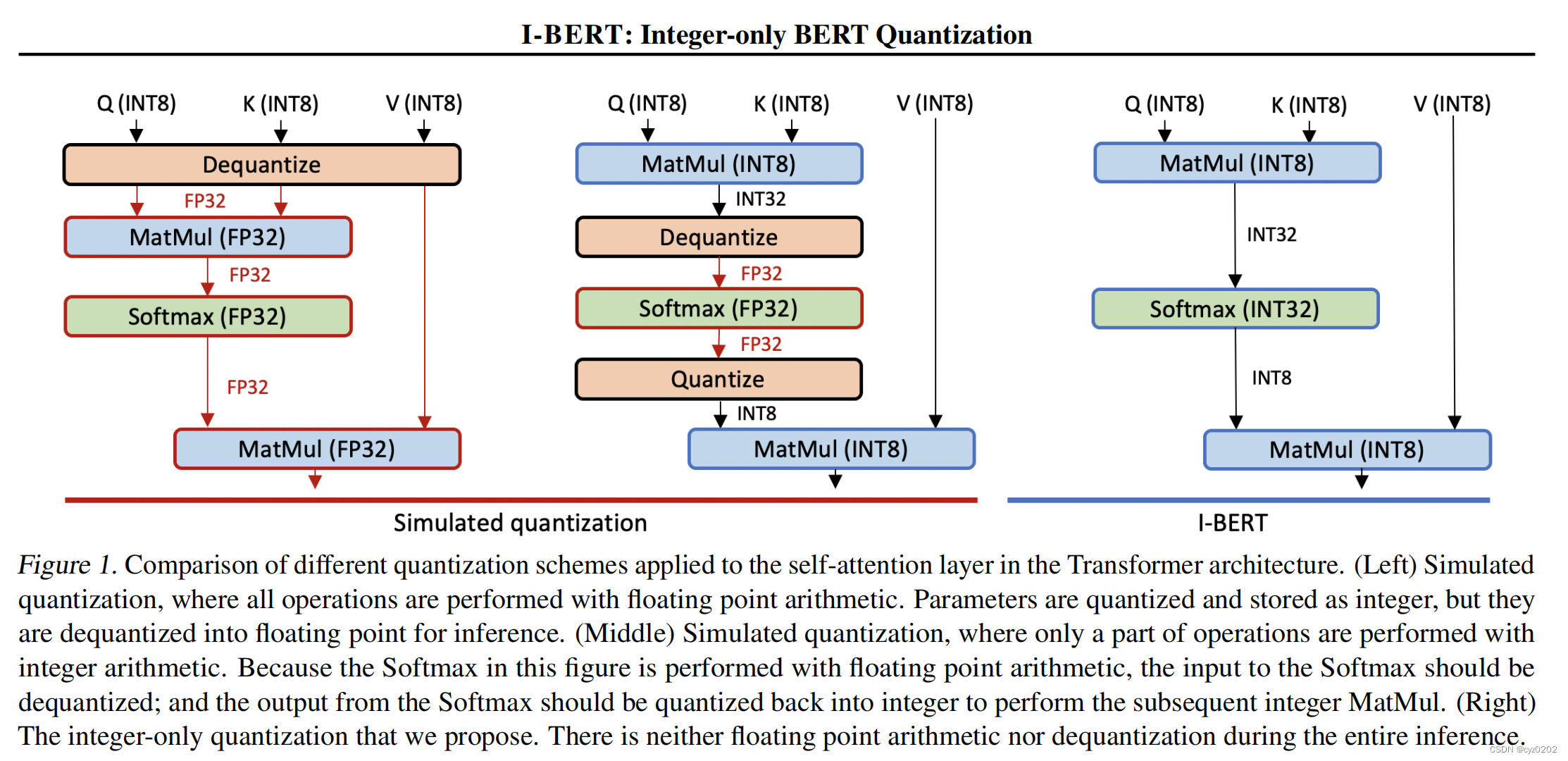
作者采用的量化方案是 8bits 对称量化;
已有方案和不足
作者主要解决GELU、softmax这两类非线性层的量化问题;
先来看看GELU的表达式,如下,erf被称为error function
![\\GELU(x) = x*\frac{1}{2}[1+erf(\frac{x}{\sqrt2})]](http://img.inotgo.com/imagesLocal/202207/06/202207060850360827_31.gif)
其中 ![\\ erf=\frac{2}{\sqrt\pi}\int^x_0e^{-t^2}dt \in [-1, 1] \\](http://img.inotgo.com/imagesLocal/202207/06/202207060850360827_19.gif)
且 
GELU本身难以直接实现量化,强行量化会导致较大精度损失;
不像线性层(如矩阵乘积、分段线性的RELU等),利用线性性质可以较好地反量化到float计算结果( 作者举例 MatMul(Sq) = S*MatMul(q),其中x=Sq,S为scale,q为x的量化值 );
已有的一些近似GELU的方案,包括:
- sigmoid近似,如下,引入非线性sigmoid,仍然不好整型计算

- ReLU6近似,如下,使用ReLU6,虽然可以整型化,但是效果不佳;该方案也被称为h-GELU

下图2左图展示了h-GELU的缺点
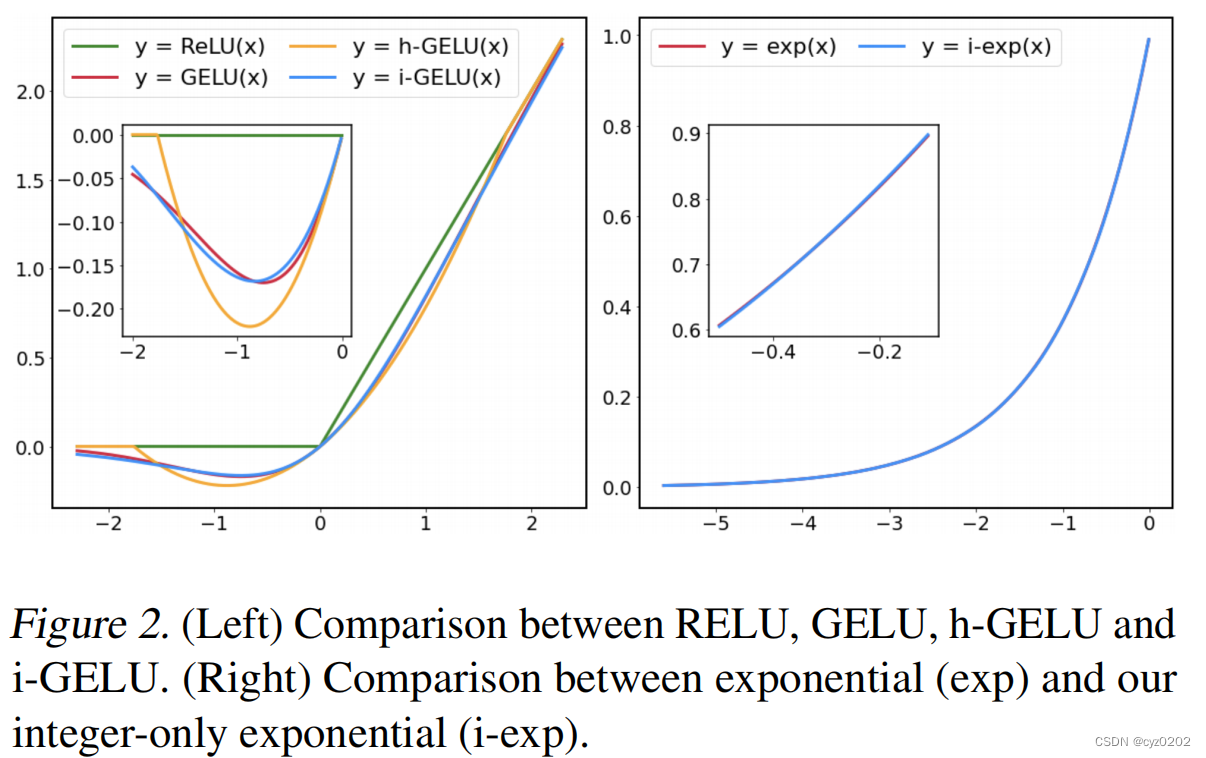
GELU的解决方案
作者通过分析,认为可以引入二阶多项式对erf进行近似,进一步对GELU进行近似,计算方式如下
![\\\underset{a,b,c}{min}\frac{1}{2}||GELU(x) - x*\frac{1}{2}[1+L(\frac{x}{\sqrt2})]||^2_2\\ s.t. \space\ \space\ \space\ L(x) = a(x+b)^2 + c](http://img.inotgo.com/imagesLocal/202207/06/202207060850360827_7.gif)
这个想法来自于任意函数可由多项式函数拟合的理论,将该类型多项式称为interpolating polynomials(插值多项式);详情请移步原文;
直接优化上式得到的结果并不理想,原因是erf的定义域是实域范围;
考虑到erf的值域在[-1, 1],且erf是个奇函数,即

因此作者通过设计正实数域部分,并推广到负实数域,得到如下L(x),
![\\L(x) = sgn(x)*\{a*[clip(|x|, max=-b) + b]^2 + 1\}](http://img.inotgo.com/imagesLocal/202207/06/202207060850360827_29.gif) ,其中
,其中

clip中的max表示|x|最大取值为-b;
因此![L(x) \in [-1, 1]](http://img.inotgo.com/imagesLocal/202207/06/202207060850360827_14.gif) ,且为奇函数;
,且为奇函数;
a、b是通过找一些GELU上的点来进行拟合求解的;
如上可得,
![i-GELU(x) := x*\frac{1}{2}[1 + L(\frac{x}{\sqrt2})]](http://img.inotgo.com/imagesLocal/202207/06/202207060850360827_18.gif)
i-GELU的量化方案
有了GELU的多项式表达形式,就可以开始设计量化方案了;
L(x)是个多项式,因此得先知道怎么对多项式量化;
作者给出了多项式量化算法 I-POLY,如下

可以验证  ,
,
因此任意2阶多项式的量化、反量化都可以采用上述算法;
(注:个人感觉这里的量化属于一种为了计算量化而量化;计算过程没问题,就是感觉是故意构造出来的那种,q_out和S_out都未必是多项式结果的真实量化值和scale)
------
有了多项式量化方法,就可以继续实现I-GELU的量化方案了,计算过程如下

调用栈为 I-GELU -> I-ERF -> I-POLY
注意图4算法中的一些实现小技巧,如
 ,
,

注意到上式 max=-b/S,可能得改成 max=round(-b/S),不然q’没法保证是整型。。。
------
以上即为I-GELU的实现过程,效果如下
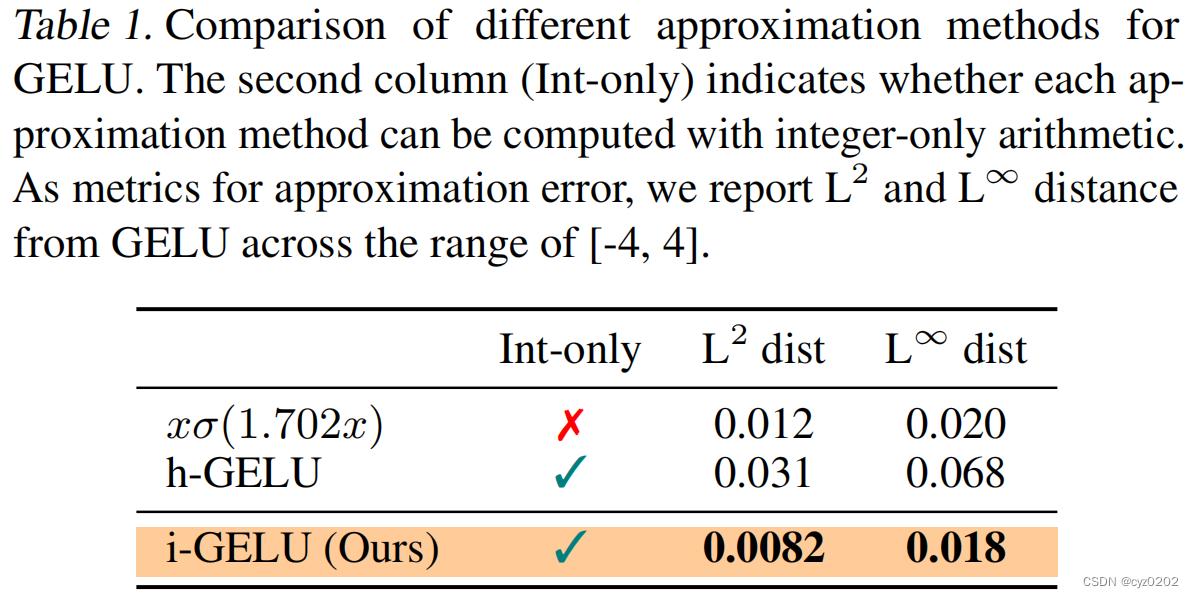
SOFTMAX的解决方案
- 利用高阶多项式进行近似,可用场景很有限;
SOFTMAX的量化方案
为了数值稳定性,作者首先对softmax进行处理,如下


值得一提的是,
对于一个非正实数 ,可以通过下式对其进行近似
,可以通过下式对其进行近似

其中z(商)是一个非负整数,p(余数)取值范围 ![(-ln2, 0]](http://img.inotgo.com/imagesLocal/202207/06/202207060850360827_22.gif) ;
;
则有

上式 >> 表示右移操作;
进一步,如果能将 表示为整型计算,那么就能对所有
表示为整型计算,那么就能对所有 以及Softmax进行整型计算了;
以及Softmax进行整型计算了;
而且  中 p的取值范围 相对x或者
中 p的取值范围 相对x或者 缩小了很多,可以更好地做近似;
缩小了很多,可以更好地做近似;
回想GELU,作者提出通过 2阶多项式近似非线性函数;这里也可以这样做;
作者寻找 的近似二阶多项式的方法,是通过在
的近似二阶多项式的方法,是通过在![(-ln2, 0]](http://img.inotgo.com/imagesLocal/202207/06/202207060850360827_22.gif) 范围内计算下式最优解:
范围内计算下式最优解:

最终得到

则

其中  ,
,
图2右图展示了上述近似有着很好的效果;
多项式的量化计算方法 I-POLY 在上面已经介绍过了,所以整个Softmax的量化计算方法为

基本思想和I-GELU差不多
#TODO#:最后一步  好像有点问题。。。
好像有点问题。。。
LayerNorm的量化方案
- 待续
I-BERT的实现解析
- 将放在另一篇文章中讨论
总结
- 本文介绍了I-BERT的改进点及 GELU/SOFTMAX 的整型化计算 实现方法;
- 主要思想是通过2阶多项式进行近似,再对2阶多项式进行量化计算;
边栏推荐
- The network model established by torch is displayed by torch viz
- Hutool gracefully parses URL links and obtains parameters
- 【嵌入式】使用JLINK RTT打印log
- Mongodb installation and basic operation
- C语言双指针——经典题型
- Deep analysis of C language pointer
- marathon-envs项目环境配置(强化学习模仿参考动作)
- How to effectively conduct automated testing?
- 多元聚类分析
- Computer cleaning, deleted system files
猜你喜欢
Promise 在uniapp的简单使用

Deep analysis of C language pointer
Image, CV2 read the conversion and size resize change of numpy array of pictures

Mobile phones and computers on the same LAN access each other, IIS settings
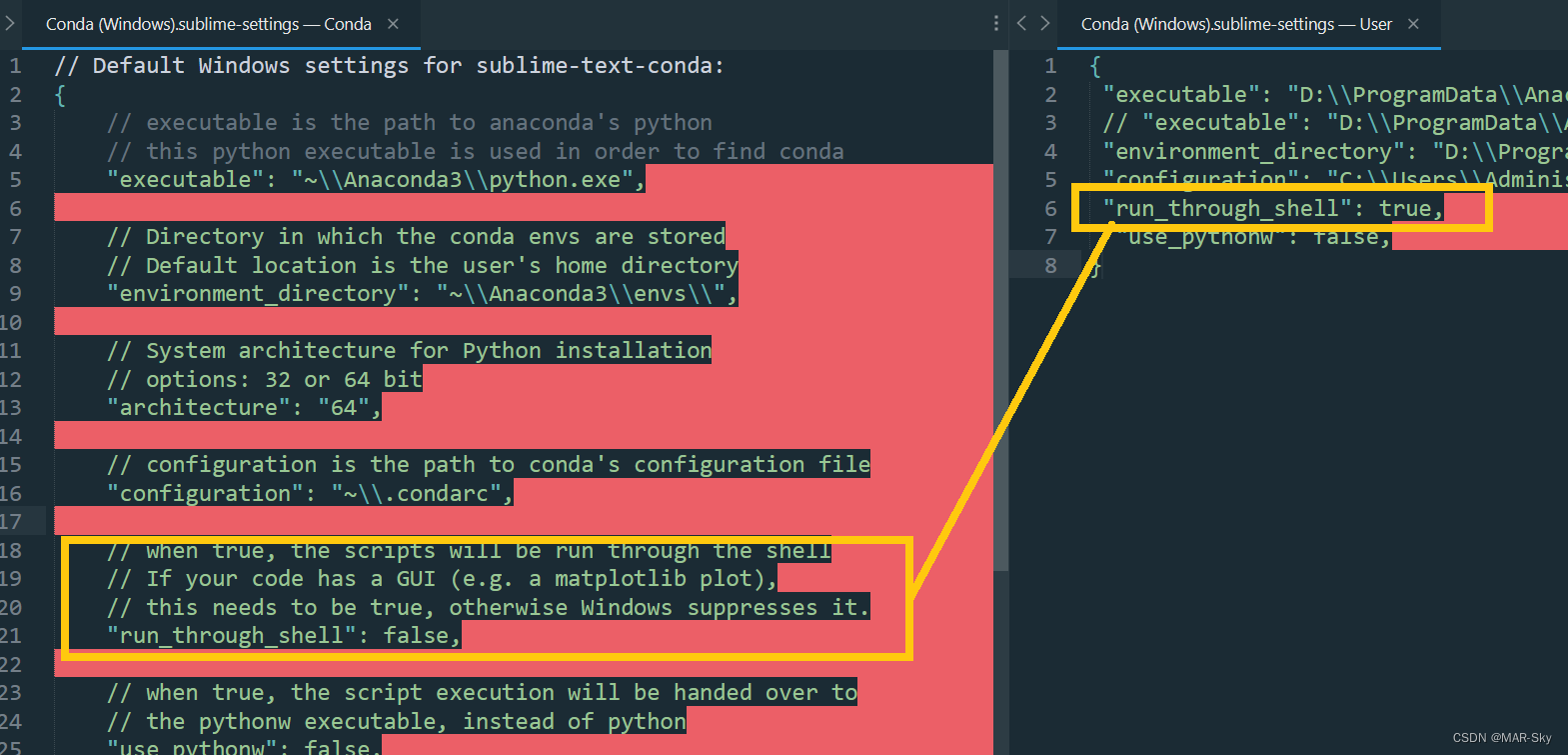
Sublime text in CONDA environment plt Show cannot pop up the problem of displaying pictures
Problems encountered in connecting the database of the project and their solutions
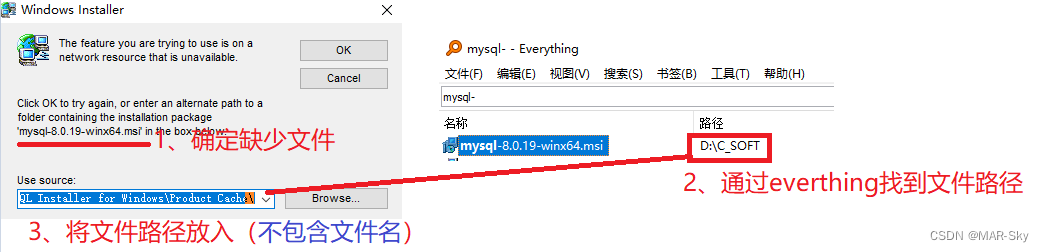
软件卸载时遇到trying to use is on a network resource that is unavailable
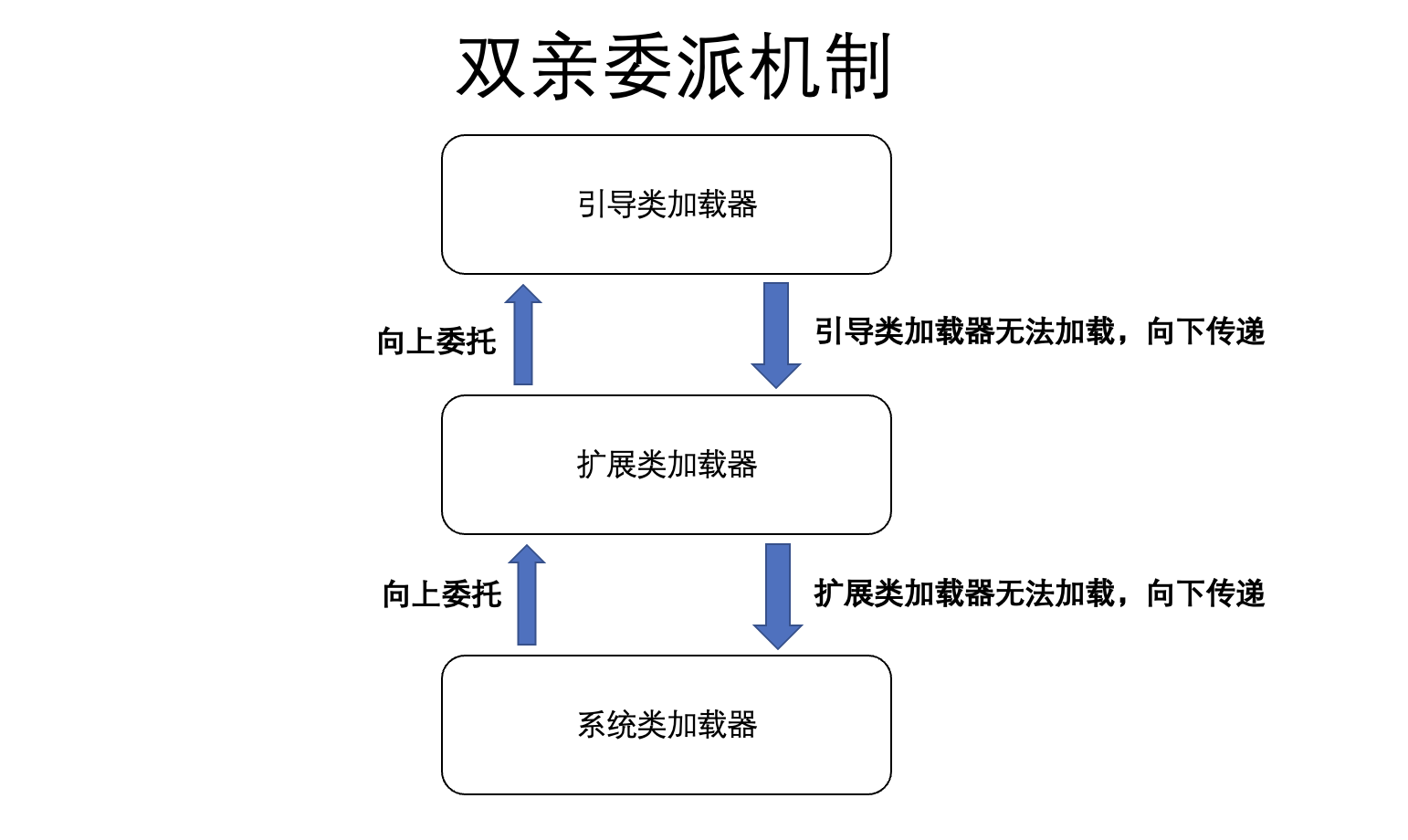
JVM quick start
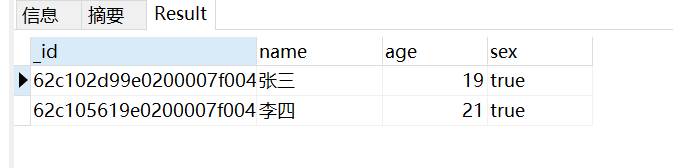
Mongodb installation and basic operation
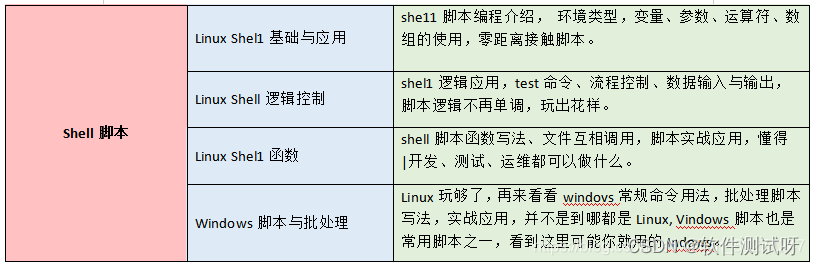
Excellent software testers have these abilities
随机推荐
目标检测——Pytorch 利用mobilenet系列(v1,v2,v3)搭建yolov4目标检测平台
同一局域网的手机和电脑相互访问,IIS设置
Problems encountered in connecting the database of the project and their solutions
Computer graduation design PHP Zhiduo online learning platform
Leetcode刷题题解2.1.1
使用latex导出IEEE文献格式
MYSQL卸载方法与安装方法
C语言双指针——经典题型
[MySQL] limit implements paging
704 binary search
【嵌入式】Cortex M4F DSP库
LeetCode:41. Missing first positive number
View computer devices in LAN
Visual implementation and inspection of visdom
Trying to use is on a network resource that is unavailable
vb.net 随窗口改变,缩放控件大小以及保持相对位置
LeetCode:124. 二叉树中的最大路径和
C language double pointer -- classic question type
Chapter 1 :Application of Artificial intelligence in Drug Design:Opportunity and Challenges
Variable length parameter