704 binary search

704. Two points search

Force button topic link

Given a n The elements are ordered （ Ascending ） integer array nums And a target value target , Write a function search nums Medium target, If the target value has a return subscript , Otherwise return to -1.

Example 1:

 Input : nums = [-1,0,3,5,9,12], target = 9     
 Output : 4       
 explain : 9  Appear in the  nums  And the subscript is  4     

Example 2:

 Input : nums = [-1,0,3,5,9,12], target = 2     
 Output : -1        
 explain : 2  non-existent  nums  So back to  -1        

Tips ：

• You can assume nums All elements in are not repeated .
• n Will be in [1, 10000] Between .
• nums Each element of will be in [-9999, 9999] Between .

Ideas

For in Ordered non repeating array Find the problem of target value in , You can consider binary search to achieve .

The title says ,nums All elements in are No repetition Of , And nums Press Ascending order , So you can consider using binary search .

The logic of binary search is relatively simple , But it is easy to make mistakes in the treatment of boundary conditions . for example , We write while(left < right) and while(left <= right) The corresponding processing method is completely different .

Let's take a simple example , Suppose there is only one element in the array 5, The target target Also equal to 5. If you use while(left < right) Writing , that right Should be initialized to 1,left Initialize to 0. And if you use while(left <= right) How to write it ,left and right Should be initialized to 0. So the difference between the two ways of writing lies in Treatment of boundary conditions .

So according to the treatment of boundary conditions , There are two ways to write binary search .

The first way to write it

Suppose the array element is [1,2,3,4,5,6,7],target = 3, We use while(left < right) Writing to achieve binary sorting .

In this way ,left = 0,right = 7, The operation process is shown in the figure

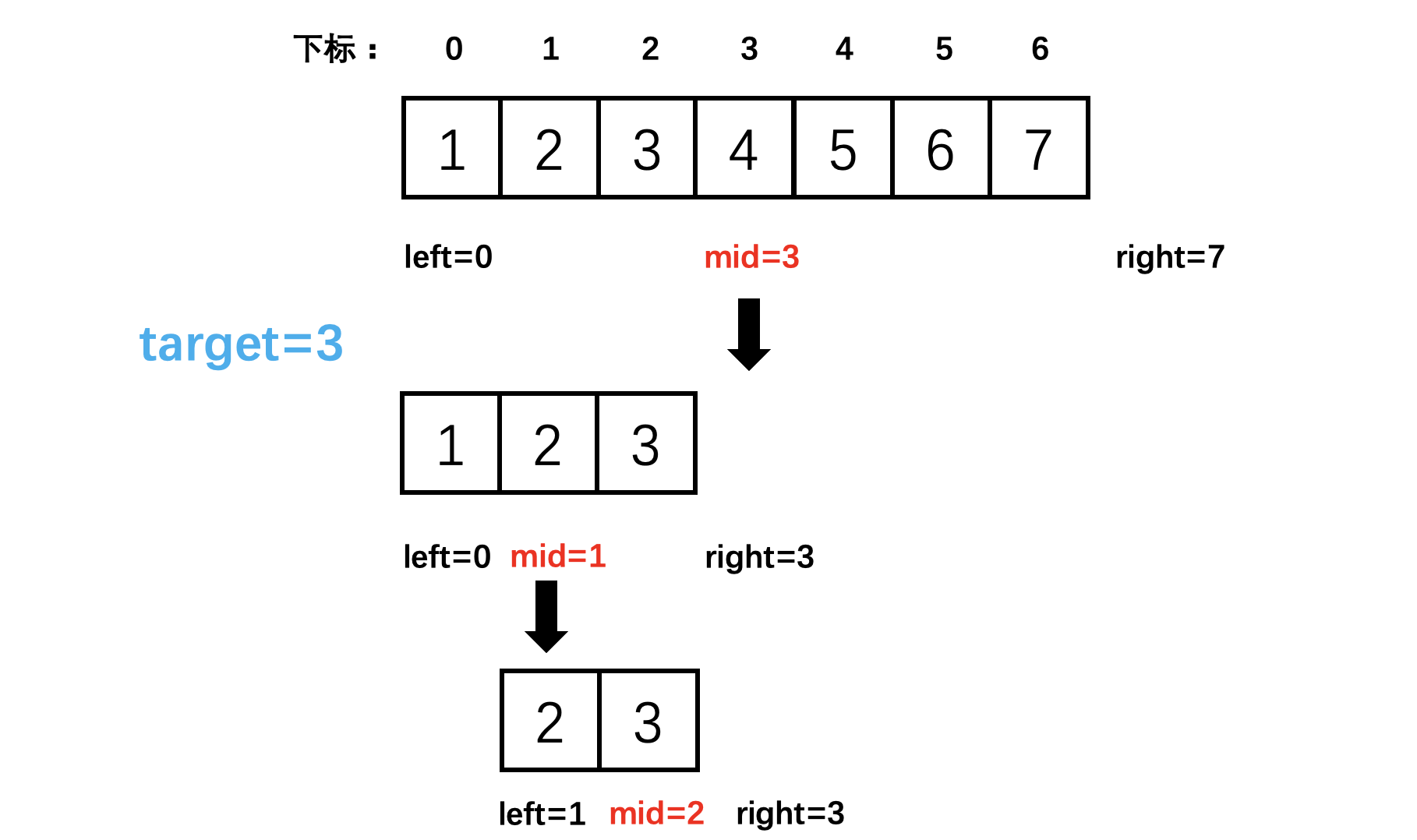
The key to the code is , When nums[mid] < nums[right] when ,right = mid. In circulation right It's open range , This should also be an open interval , bring into correspondence with .

The corresponding code is as follows :（Kotlin）

class Solution {
    fun search(nums: IntArray, target: Int): Int {
        var left = 0
        var right = nums.size // [left,right)  On the right is the open section ,right  Set to  nums.size
        while (left < right) {
            val mid = (left + right) / 2
            if (nums[mid] < target) left = mid + 1
            else if (nums[mid] > target) right = mid //  The core of the code , In circulation  right  It's open range , This should also be an open interval 
            else return mid
        }
        return -1 //  Can't find  target , return  -1
    }
}

The second way

Suppose the array element is [1,2,3,4,5,6,7],target = 3, We use while(left <= right) Writing to achieve binary sorting .

In this way ,`left = 0,right = 76, The operation process is shown in the figure

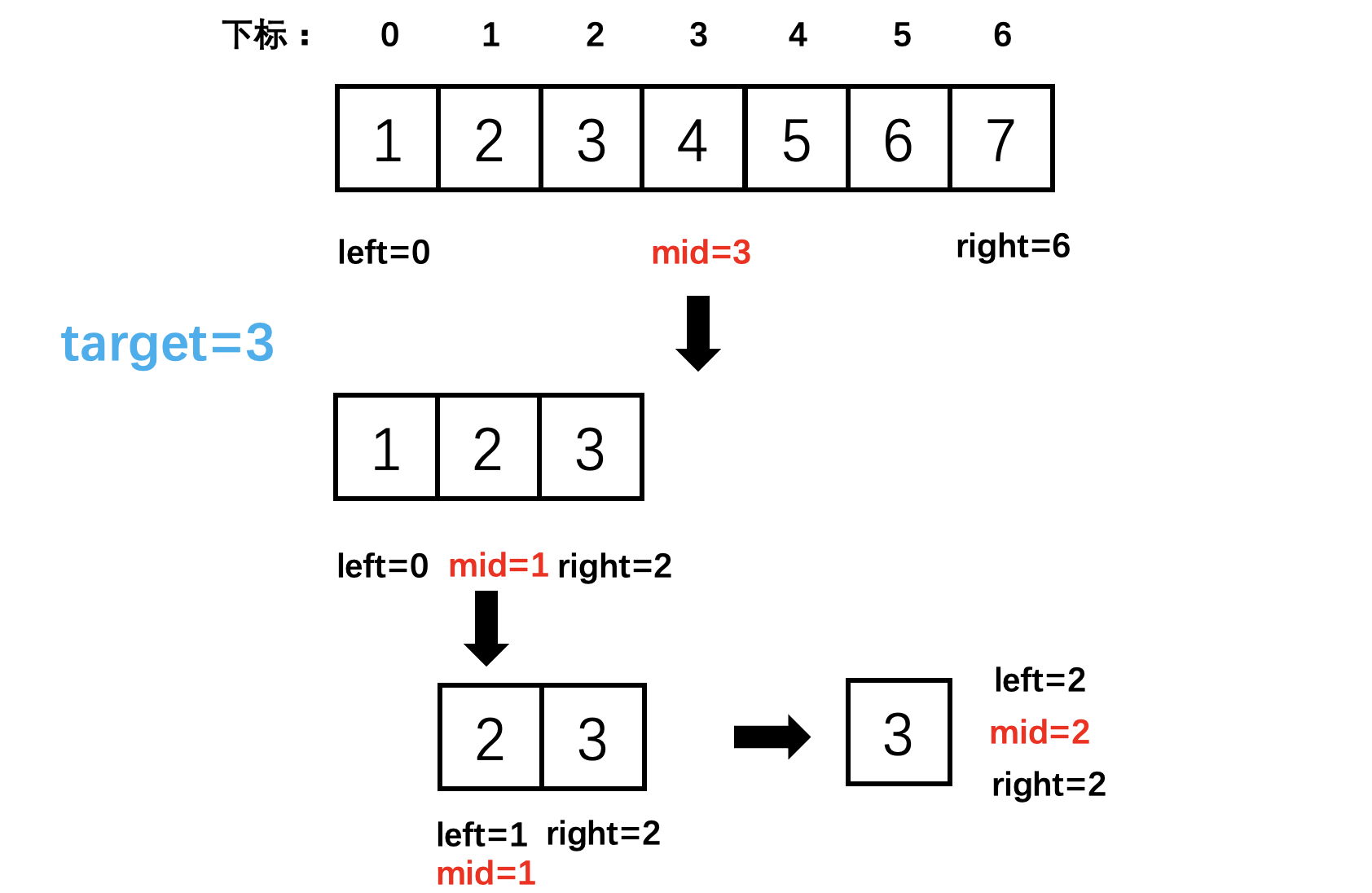
The key to the code is , When nums[mid] < nums[right] when ,right = mid - 1. In circulation right It's a closed interval , This should also be a closed interval , bring into correspondence with .

The corresponding code is as follows :（Kotlin）

class Solution {
    
    fun search(nums: IntArray, target: Int): Int {
    
        var left = 0
        var right = nums.size - 1 // [left,right]  The right side is the closed section ,right  Set to  nums.size - 1
        while (left <= right) {
    
            val mid = (left + right) / 2
            if (nums[mid] < target) left = mid + 1
            else if (nums[mid] > target) right = mid - 1 //  The core of the code , In circulation  right  It's a closed interval , This should also be a closed interval 
            else return mid
        }
        return -1 //  Can't find  target , return  -1
    }
}