当前位置:网站首页>Line segment tree blue book explanation + classic example acwing 1275 Maximum number
Line segment tree blue book explanation + classic example acwing 1275 Maximum number
2022-07-03 20:19:00 【Jacob* ̄▽ ̄*】
Introduction to segment tree
Segment tree is a kind of tree based on Divide and conquer thoughts Of Binary tree structure , It is used for information statistics on the interval .
And in accordance with “2 Power of power ” Divided Tree array comparison , Segment tree is a kind of More general Data structure of :
- ① Line segment tree Each node represents an interval
- ② Of the line segment tree The root node is unique , The interval represented is The whole statistical range , Such as :
[1, N] - ③ Segment tree each Leaf node Both represent a length of
1Of Unit interval[x, x] - ④ about Every internal node
[l, r], Its Left son yes[l, mid], Right son yes[mid+1, r], amongmid=l+r>>1( namely(l+r)/2Rounding down )
Interval Perspective Line segment tree under :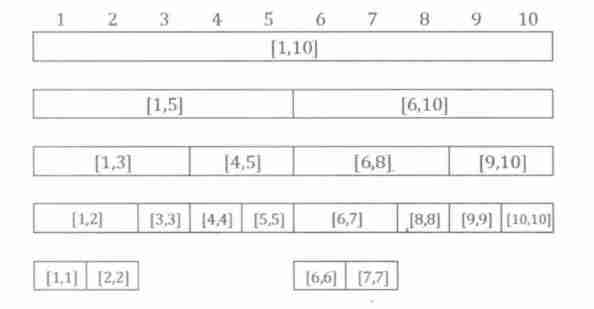
Binary tree view Line segment tree under :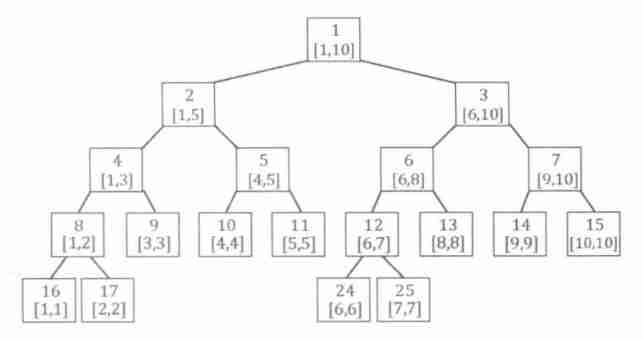
As shown in the figure above Line segment tree , If Remove the last layer , The whole tree must be a Perfect binary tree , And the depth is O(logN). So we can follow what we learned before , And Binary heap Allied Father and son 2 times Node number Method :
- ① The root node number is
1 - ② The number is
xThe left son of the node is numberedx<<1, The right son isx<<1|1
So we can use one Array of structs To store the entire segment tree .
Of course , Treelike The last layer The storage location of the node in the structure array is Discontinuous Of , Just empty the redundant position of the array .
In an ideal situation ,N A leaf node Full binary tree Yes N + N/2 + N/4 + ... + 2 + 1 = 2N - 1 Nodes .
Because under the above storage mode , The last layer produces redundancy ( At most 2N Nodes ), Therefore, the length of the array storing the segment tree should not be less than 4N(2N - 1 + 2N = 4N - 1) Only in this way can we ensure that we don't cross the line !
One 、 The construction of line segment tree :build
The basic purpose of segment tree is to A sequence a For maintenance , Support Inquire about ask and modify modify Instructions .
Given a length of N Of a Sequence , We can be in the interval [1, N] Build a segment tree on . Every leaf node [i, i] preservation a[i] Value .
Of the line segment tree Binary tree structure It's very convenient to From bottom to top Transmit information , about “ From bottom to top ”, namely The son node calculates the father node information , We can write a pushup function , We use Interval maximum As an example :
Recording interval [l, r] The maximum value is dat(l, r) = max{a[l], a[l+1], ..., a[r]},
obviously dat(l, r) = max(dat(l, mid), dat(mid+1, r))(mid = l+r>>1).
If the sequence used to build the heap a = {3, 6, 4, 8, 1, 2, 9, 5, 7, 0}, We can use build(1, 1, 10), From the root node "1" Start , In the sequence a Of [1, 10] A segment tree is established in this interval, as shown in the figure below :
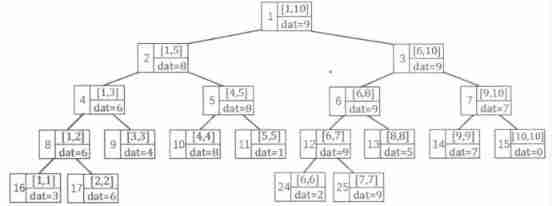
Let's first write a for storing segment trees Array of structs :
struct node
{
int l, r;// The left side of the interval 、 Right border
int dat;// Section [l, r] Maximum
} t[4*N];// The structure array stores the line segment tree , The size is at least the original sequence a Of 4 times
pushup function :
// The son node calculates the father node information
void pushup(int u) {t[u].dat = max(t[u<<1].dat, t[u<<1|1].dat);}
build function :
void build(int u, int l, int r)// Establish a segment tree and save the maximum value of the corresponding interval on each node max
{
t[u].l = l, t[u].r = r;// node u Represents the interval [l, r]
if(l==r) {t[p].dat = a[l]; return ;}// If the current leaf node is directly return
int mid = l+r>>1;// The midpoint of the current interval
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
// Recursively establish the left section respectively [l, mid], Number u<<1 Right section [mid+1, r], Number u<<1|1
pushup(u);
}
call build Function entrance :
build(1, 1, n);// From the root node "`1`" Start , In the sequence `a` Of `[1, n]` This section establishes a segment tree
Two 、 Line tree single point modification :modify
The single point modification instruction is shown in “C x v”, Express hold a[x] It is amended as follows v.
In the line tree , The root node ( The number is 1 The node of ) It is the entrance to execute various instructions .
from The root node set out , recursive Find the representative interval [x, x] Leaf node of , Then update from bottom to top [x, x] And the information stored on all its ancestor nodes . Here's the picture , show modify(1, 7, 1), The shaded part is the node that needs to be changed .
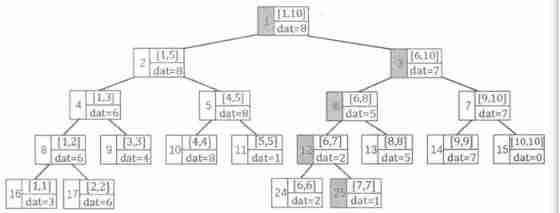
modify function : Time complexity :O(logN)
// Starting from the root node , Recursively find the representative interval [x, x] Leaf node of , Then update from bottom to top [x, x]
// And the information stored on all its ancestor nodes .
void modify(int u, int x, int v)// Single point modification hold a[x] Is changed to v
{
if(t[u].l==x&&t[u].r==x) {t[u].dat = v; return ;}// If you find a leaf node, modify it directly
// Otherwise, judge whether to recurse to the left or to the right
int mid = t[u].l+t[u].r>>1;// Take the midpoint
if(x<=mid) modify(u<<1, x, v);//x Belongs to the left
else modify(u<<1|1, x, v);//x Belongs to the right
// When the recursion is complete , Remember to update the maximum value information of the current node
pushup(u);// Go back and update information from bottom to top
}
call modify Function entrance :
modify(1, x, v);// Starting from the root node , take a[x] Is changed to v
3、 ... and 、 Interval query of line segment tree :ask
The interval query instruction is shaped like “Q l r”, Express Query sequence a In the interval [l, r] Maximum on , namely max{a[l], a[l+1], ..., a[r]}.
We Start at the root node , Execute the procedure recursively :
- ① if
[l, r]Completely cover the representative interval of the current node , Go back now , And this nodedatValue is the candidate answer . - ② If left son and
[l, r]There is intersection , Recursive access to the left son .
③ If the right son and[l, r]There is intersection , Recursive access to right son .
Pictured : perform ask(1, 2, 8) = max{6, 4, 8, 5} = 8, Section [2, 8] It contains exactly four shadow nodes .

ask function : Time complexity :O(logN)
int ask(int u, int l, int r)// Maximum value of interval query max
{
if(l<=t[u].l&&r>=t[u].r) return t[u].dat;// Nodes in the tree , It has been completely included in [l, r] It's in
int mid = t[u].l+t[u].r>>1;
int val = -(1<<30);// Negative infinity
if(l<=mid) val = max(val, ask(u<<1, l, r));// There is intersection with the left
if(r>=mid+1) val = max(val, ask(u<<1|1, l, r));// There is an intersection with the right
return val;
}
call ask Function entrance :
cout<<ask(1, l, r)<<endl;// From the root node "1" Start , Inquire about [l, r] Max in
Can prove that , The above query process will ask the interval [l, r] It is divided into O(logN) Nodes , Take their maximum As the answer .
above , It is about the explanation of line segment tree .
Example :AcWing 1275. The maximum number


The question :

Ideas :
Use the line segment tree to realize two operations :
Q L: Ask the last in the sequence L What is the maximum number of numbers A t: To add a number to the sequence , What's the number (t+a) mod p. among ,t Is the input parameter ,a It's the last one to ask for the answer before the add operation ( If you didn't ask about the operation before , be a=0)
Due to input instructions “A t” At the time of revision The value used t And the value of the last query a It matters , So this question is Dynamic problems , We cannot use static methods , Read them all first, preprocess them again, and then deal with them , Only by knowing the answer to the previous question can we know how many people are currently ready to join .
There is no sequence in this question a To initialize the segment tree , Therefore, the initial direct first build One is all 0 Line segment tree of .
After that, it is basically the basic operation of the line segment tree mentioned above .
Time complexity :
O(mlogm)
Blank code :
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5+10;
int m, p;
struct node
{
int l, r;
int dat;
} t[4*N];
void pushup(int u) {t[u].dat = max(t[u<<1].dat, t[u<<1|1].dat);}
void build(int u, int l, int r)
{
t[u].l = l, t[u].r = r;
if(l==r) return ;
int mid = l+r>>1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
}
void modify(int u, int x, int v)
{
if(t[u].l==x&&t[u].r==x) {t[u].dat = v; return ;}
int mid = t[u].l+t[u].r>>1;
if(x<=mid) modify(u<<1, x, v);
else modify(u<<1|1, x, v);
pushup(u);
}
int ask(int u, int l, int r)
{
if(l<=t[u].l&&r>=t[u].r) return t[u].dat;
int mid = t[u].l+t[u].r>>1;
int val = -(1<<30);
if(l<=mid) val = max(val, ask(u<<1, l, r));
if(r>=mid+1) val = max(val, ask(u<<1|1, l, r));
return val;
}
signed main()
{
int now = 0;
int last = 0;
cin>>m>>p;
build(1, 1, m);
int x;
char op[2];
while(m--)
{
scanf("%s%d", op, &x);
if(*op=='Q')
{
last = ask(1, now-x+1, now);
printf("%d\n", last);
}
else
{
modify(1, now+1, (last+x)%p);
++now;
}
}
return 0;
}
Comment code :
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5+10;
int m, p;// Operands and modulo numbers
//node Structure
struct node
{
int l, r;
int dat;// Section [l, r] Maximum
} t[4*N];// The structure array stores the line segment tree
//pushup function
// The son node calculates the father node information
void pushup(int u) {t[u].dat = max(t[u<<1].dat, t[u<<1|1].dat);}
//build function
void build(int u, int l, int r)// Establish a segment tree and save the maximum value of the corresponding interval on each node max
{
t[u].l = l, t[u].r = r;// node u Represents the interval [l, r]
if(l==r)
{
//t[p].dat = a[l];// There is no initial array for building a segment tree a, So don't use this sentence
return ;// If the current leaf node is directly return
}
int mid = l+r>>1;// The midpoint of the current interval
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
// Recursively establish the left interval [l, mid], Number u<<1 Recursively establish the right interval [mid+1, r], Number u<<1|1
//pushup(u);// When initializing the line segment tree, this problem does not give dat assignment , So there is no need for pushup
}
//modify function
// Starting from the root node , Recursively find the representative interval [x, x] Leaf node of , Then update from bottom to top [x, x]
// And the information stored on all its ancestor nodes .
void modify(int u, int x, int v)// Single point modification hold a[x] Is changed to v
{
if(t[u].l==x&&t[u].r==x) {t[u].dat = v; return ;}// If you find a leaf node, modify it directly
// Otherwise, judge whether to recurse to the left or to the right
int mid = t[u].l+t[u].r>>1;// Take the midpoint
if(x<=mid) modify(u<<1, x, v);//x Belongs to the left
else modify(u<<1|1, x, v);//x Belongs to the right
// When the recursion is complete , Remember to update the maximum value information of the current node
pushup(u);// Go back and update information from bottom to top
}
//ask function
// Start at the root node , Execute the procedure recursively :
//1. if [l, r] Completely cover the interval represented by the current node , Go back now , And the node's dat Value is the candidate answer
//2. If the left child node and [l, r] There is intersection , Then recursively access the left child node
//3. If the right child node and [l, r] There is intersection , Then recursively access the right child node
int ask(int u, int l, int r)// Maximum value of interval query max
{
if(l<=t[u].l&&r>=t[u].r) return t[u].dat;// Nodes in the tree , It has been completely included in [l, r] It's in
int mid = t[u].l+t[u].r>>1;
int val = -(1<<30);// Negative infinity
if(l<=mid) val = max(val, ask(u<<1, l, r));// There is intersection with the left
if(r>=mid+1) val = max(val, ask(u<<1|1, l, r));// There is an intersection with the right
return val;
}
signed main()
{
int now = 0;// Number of current data
int last = 0;// Store the answer to the last question
cin>>m>>p;
build(1, 1, m);// Create a line tree , The operands are m So the maximum length is m
int x;
char op[2];
while(m--)
{
scanf("%s%d", op, &x);
if(*op=='Q')
{
last = ask(1, now-x+1, now);// Start the query from the root node , The current query interval is after x Number ,n-x+1 That is, the leftmost position of the query interval , On the far right is n
printf("%d\n", last);
}
else// Take the next position n+1 The number of changes
{
modify(1, now+1, (last+x)%p);// Start with the first number , Amendment No n+1 A place , It is amended as follows (last+x)%p
++now;
}
}
return 0;
}
边栏推荐
- Kubernetes cluster builds efk log collection platform
- IPv6 experiment
- How to check the permission to write to a directory or file- How do you check for permissions to write to a directory or file?
- unittest框架基本使用
- Instructions for common methods of regular expressions
- Global and Chinese market of charity software 2022-2028: Research Report on technology, participants, trends, market size and share
- 6006. Take out the minimum number of magic beans
- 44. Concurrent programming theory
- Xctf attack and defense world crypto advanced area best_ rsa
- Fingerprint password lock based on Hal Library
猜你喜欢

Example of peanut shell inner net penetration

Node MySQL serialize cannot rollback transactions
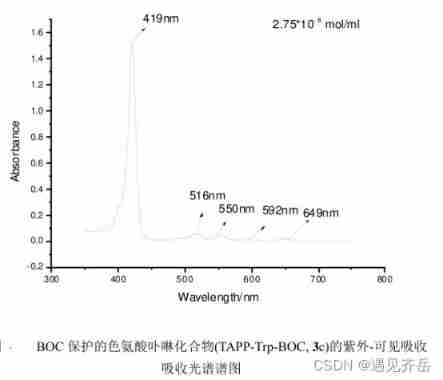
BOC protected tryptophan porphyrin compound (TAPP Trp BOC) Pink Solid 162.8mg supply - Qiyue supply
![AI enhanced safety monitoring project [with detailed code]](/img/a9/cb93f349229e86cbb05ad196ae9553.jpg)
AI enhanced safety monitoring project [with detailed code]
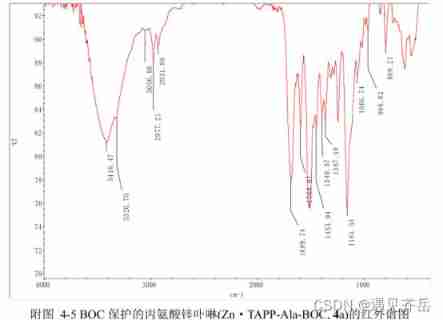
BOC protected alanine zinc porphyrin Zn · TAPP ala BOC / alanine zinc porphyrin Zn · TAPP ala BOC / alanine zinc porphyrin Zn · TAPP ala BOC / alanine zinc porphyrin Zn · TAPP ala BOC supplied by Qiyu

BOC protected tryptophan zinc porphyrin (Zn · TAPP Trp BOC) / copper porphyrin (Cu · TAPP Trp BOC) / cobalt porphyrin (cobalt · TAPP Trp BOC) / iron porphyrin (Fe · TAPP Trp BOC) / Qiyue supply

Xctf attack and defense world crypto advanced area best_ rsa

Kubernetes cluster builds efk log collection platform
2.6 formula calculation
thrift go
随机推荐
Golang type assertion and conversion (and strconv package)
Blue Bridge Cup: the fourth preliminary - "simulated intelligent irrigation system"
Network security Kali penetration learning how to get started with web penetration how to scan based on nmap
About callback function and hook function
Rd file name conflict when extending a S4 method of some other package
Meso tetra [P - (p-n-carbazole benzylidene imino)] phenylporphyrin (tcipp) /eu (tcipp) [pc( α- 2-oc8h17) 4] and euh (tcipp) [pc (a-2-oc8h17) 4] supplied by Qiyue
Deep search DFS + wide search BFS + traversal of trees and graphs + topological sequence (template article acwing)
unittest框架基本使用
Instructions for common methods of regular expressions
2.1 use of variables
Introduction to golang garbage collection
2022 Xinjiang latest road transportation safety officer simulation examination questions and answers
BOC protected amino acid porphyrins TAPP ala BOC, TAPP Phe BOC, TAPP Trp BOC, Zn · TAPP ala BOC, Zn · TAPP Phe BOC, Zn · TAPP Trp BOC Qiyue
Professional interpretation | how to become an SQL developer
原生表格-滚动-合并功能
[raid] [simple DP] mine excavation
MySQL learning notes - single table query
Wechat applet quick start (including NPM package use and mobx status management)
Recommendation of books related to strong foundation program mathematics
Use of CMD command