当前位置：网站首页>Detailed explanation of balanced binary tree is easy to understand
Detailed explanation of balanced binary tree is easy to understand
2022-07-06 12:52:00 【Deng Jiawen jarvan】
Balanced binary trees （AVL）
Please understand before reading Binary search tree
Golang The communication group pays attention to official account Deng Jiawen Jarvan
Balanced binary tree definition ： The height difference of any node's subtree is less than or equal to 1
1. Why use 「 Balanced binary trees 」
Binary tree can improve the efficiency of query O(logn), But when you insert {1,2,3,4,5,6} This kind of data , Your binary tree is like a 「 Linked list 」 equally , Search efficiency becomes O(n)
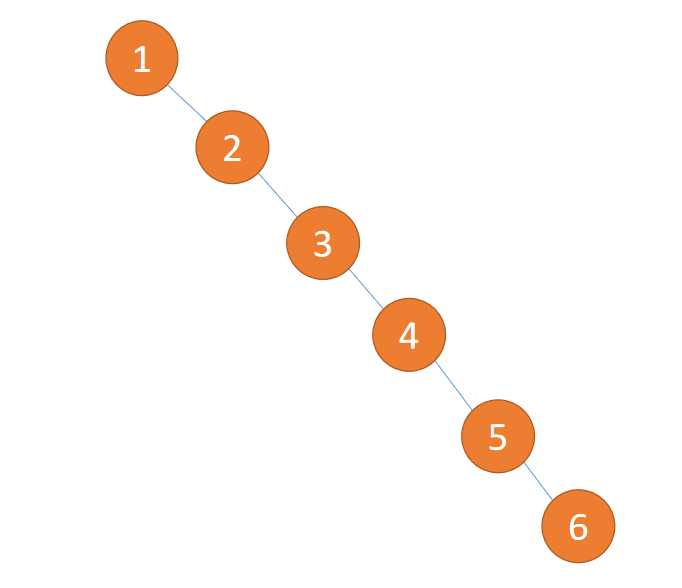
So in 1962 year , A family name AV Big guy （G. M. Adelson-Velsky） And a last name L Big guy （ Evgenii Landis） Put forward 「 Balanced binary trees 」（AVL） .
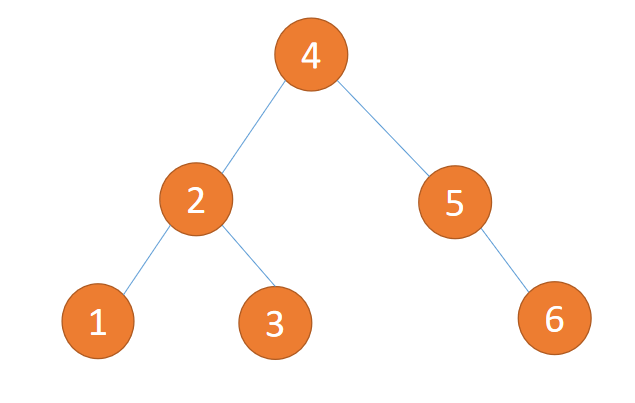
So insert {1,2,3,4,5,6} The results of this data are shown in the figure below ：
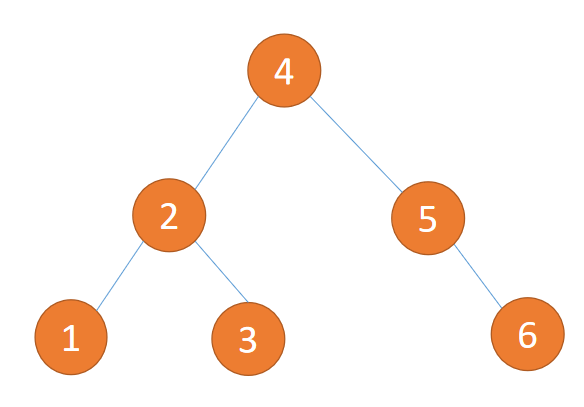
2. Judge 「 Balanced binary trees 」
Judge 「 Balanced binary trees 」 Of 2 Conditions ：
- 1. yes 「 Binary sort tree 」
- 2. The left or right subtree of any node is 「 Balanced binary trees 」（ The height difference between left and right is less than or equal to 1）
（1） The picture below is not 「 Balanced binary trees 」 Because it's not 「 Binary sort tree 」 In violation of 1 Conditions
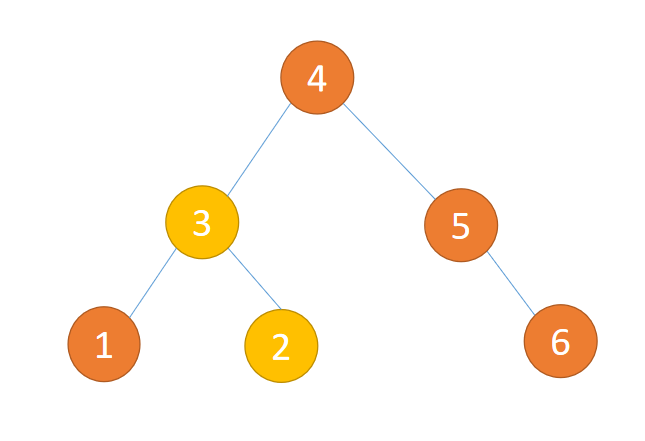
（2） The picture below is not 「 Balanced binary trees 」 Because the height difference of node subtree is greater than 1 Illegal article 2 Conditions
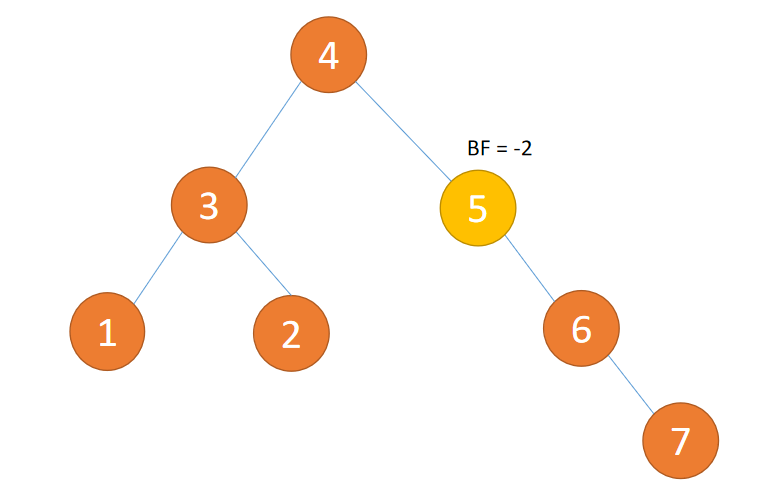
（3） The picture below is 「 Balanced binary trees 」 Because it conforms to 1、2 Conditions
3. Relevant concepts
3.1 Balance factor BF
Definition ： Height difference between left subtree and right subtree
Calculation ： Height of left subtree - The value of the height of the right subtree
Alias ： abbreviation BF（Balance Factor instead of Boy Friend）
Generally speaking BF The absolute value of is greater than 1,, A balanced tree is a binary tree , need 「 rotate 」 correct
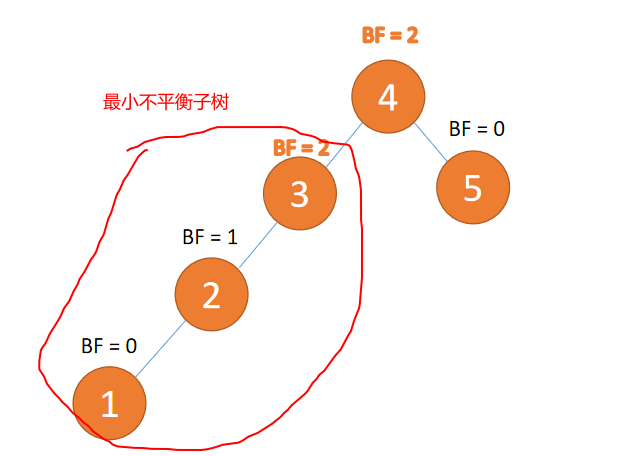
3.2 Minimum unbalanced subtree
The closest... To the insertion node , also BF The absolute value of is greater than 1 The node of is the subtree of the root node .
「 rotate 」 Correction only needs correction 「 Minimum unbalanced subtree 」 that will do
An example is shown in the figure below ：
4. Two rotation modes
2 Kind of 「 rotate 」 The way ：
- left-handed
- The old root node is the left subtree of the new root node
- The left subtree of the new root node （ If there is ） Is the right subtree of the old root node
- Right hand ：
- The old root node is the right subtree of the new root node
- The right subtree of the new root node （ If there is ） Is the left subtree of the old root node
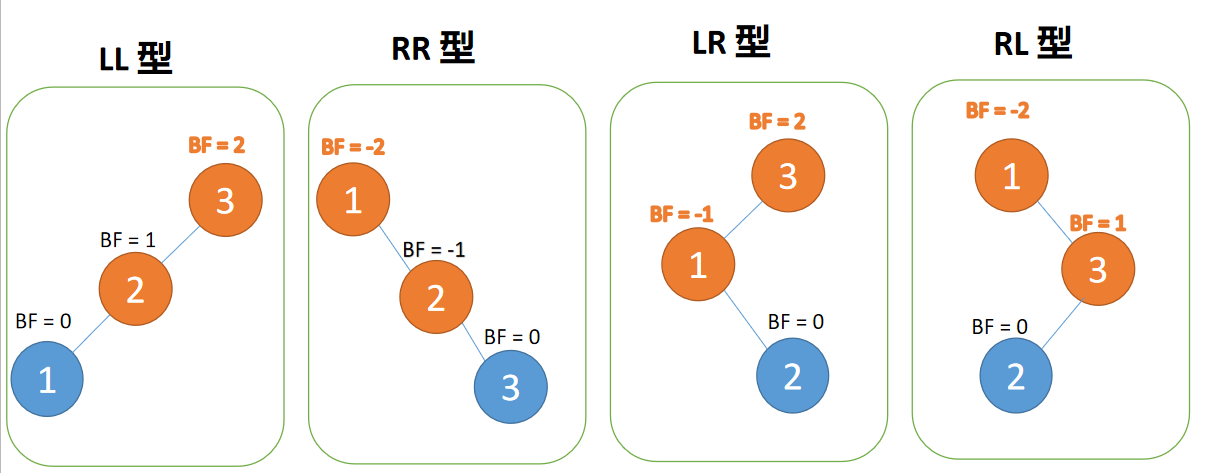
4 Kind of 「 rotate 」 Correction type ：
- LL type ： Insert the left subtree of the left child , Right hand
- RR type ： Insert the right subtree of the right child , left-handed
- LR type ： Insert the right subtree of the left child , First left , Turn right again
- RL type ： Insert the left subtree of the right child , First right , Turn left again
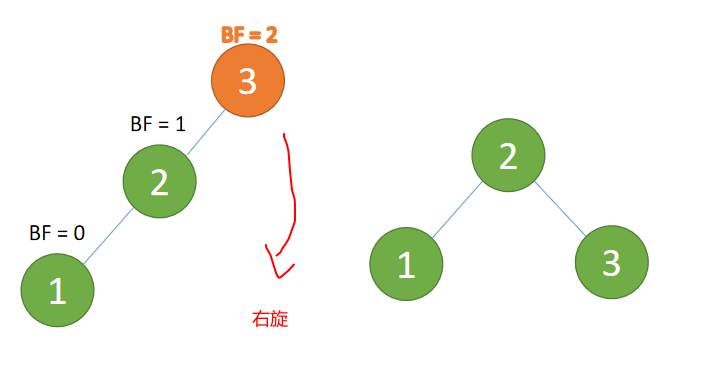
4.1 LL Type imbalance 「 Right hand 」
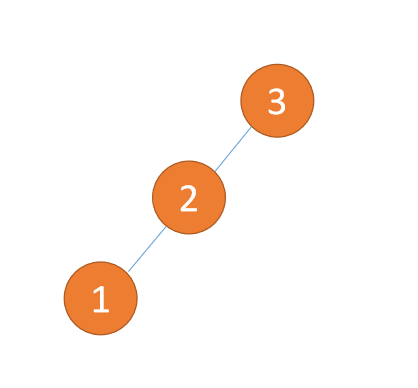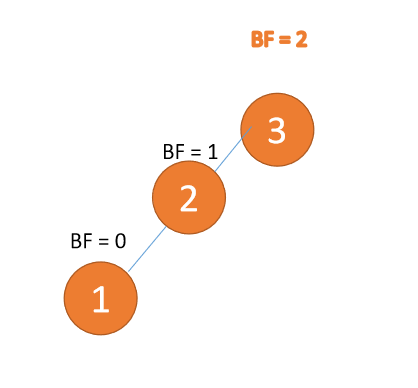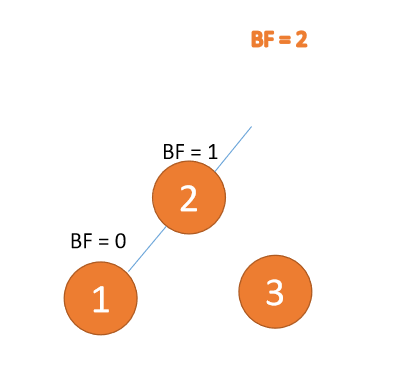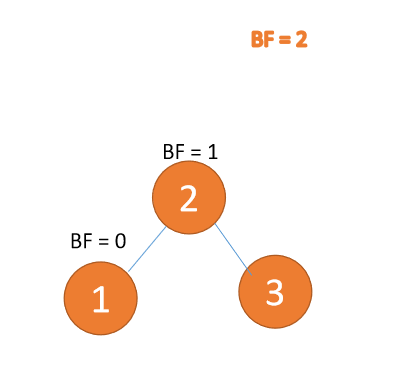
Third node 「1」 Inserted When ,BF(3) = 2,BF(2) = 1LL Type imbalance , Right hand , The root node rotates clockwise
（1） Minimum unbalanced subtree 「 Right hand 」
Right hand
- Old root node （ node 3） For the new root node （ node 2） The right subtree
- Of the new root node Right subtree （ If there is ） Is the left subtree of the old root node
4.2 RR Type imbalance 「 left-handed 」
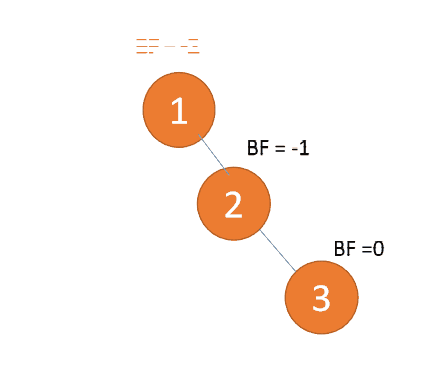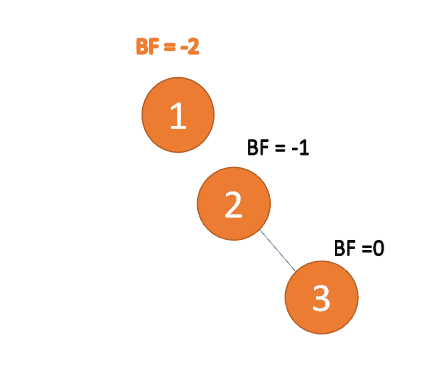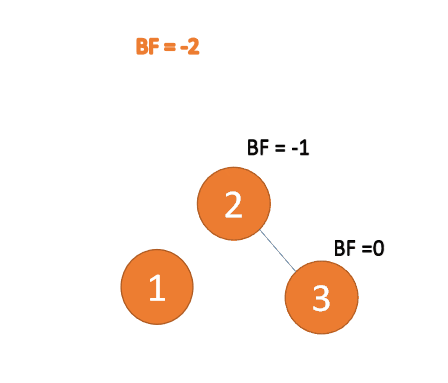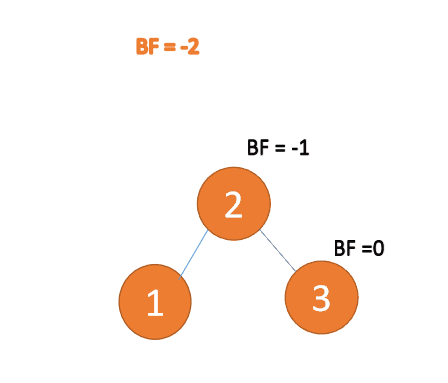
Third node 「3」 Inserted When ,BF(1)=-2 BF(2)=-1,RR Type imbalance , left-handed , The root node rotates counterclockwise
（1） The minimum unbalanced subtree is left-handed
left-handed
- Old root node （ node 1） For the new root node （ node 2） The left subtree
- The left subtree of the new root node （ If there is ） Is the right subtree of the old root node
4.3 LR type
Third node 「3」 Inserted When ,BF(3)=2 BF(1)=-1LR Type imbalance , First 「 left-handed 」 Again 「 Right hand 」
（1） Minimum unbalanced subtree left subtree {2,1} First left
left-handed
- Old root node （ node 1） For the new root node （ node 2） The left subtree
- The left subtree of the new root node （ If there is ） Is the right subtree of the old root node
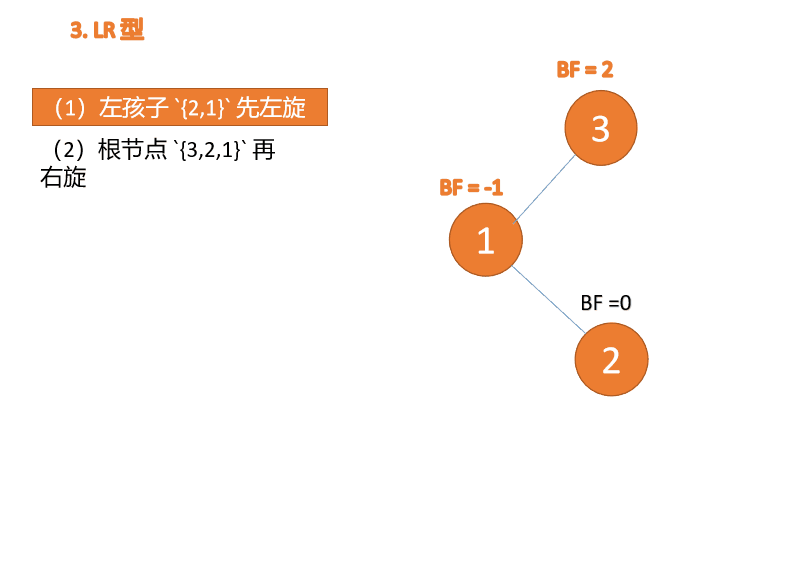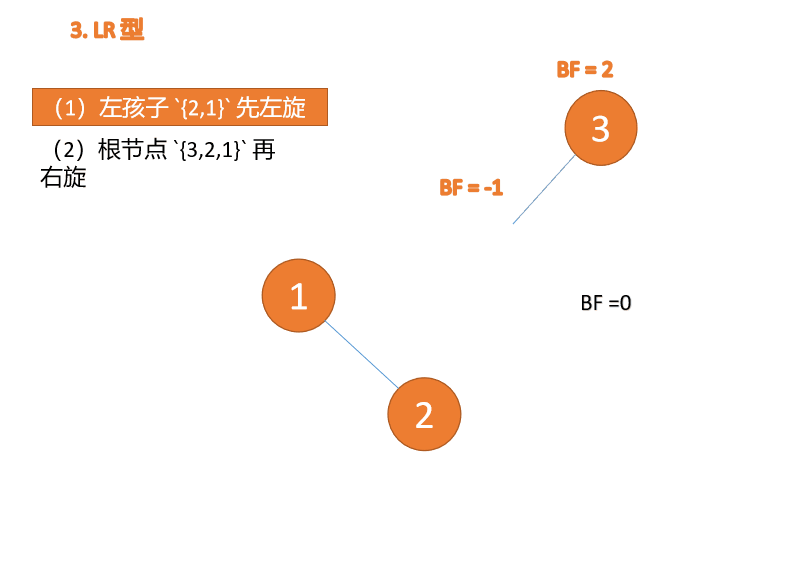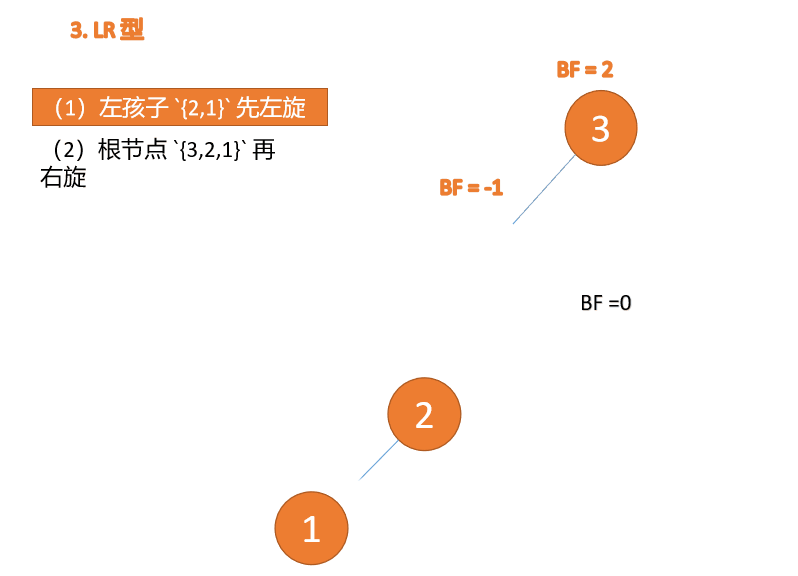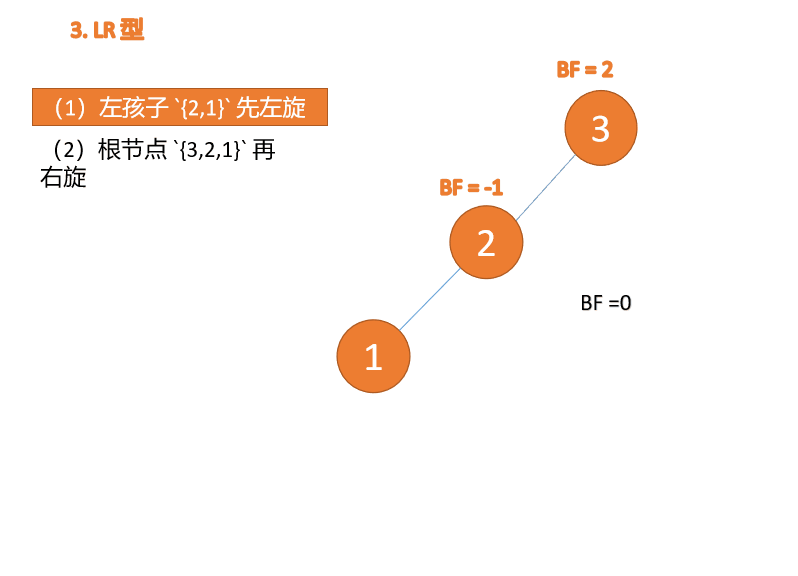
（2） Minimum unbalanced subtree {3,2,1} Turn right again
Right hand
- Old root node （ node 3） For the new root node （ node 2） The right subtree
- Of the new root node Right subtree （ If there is ） Is the left subtree of the old root node
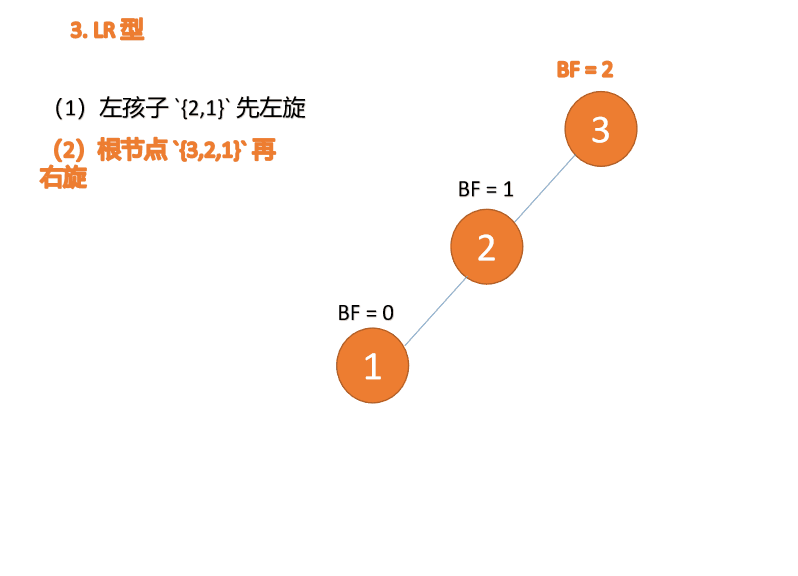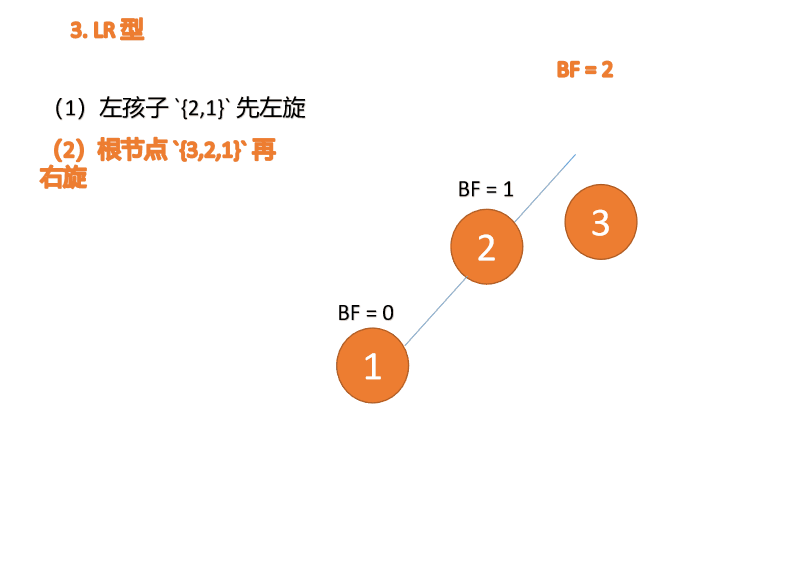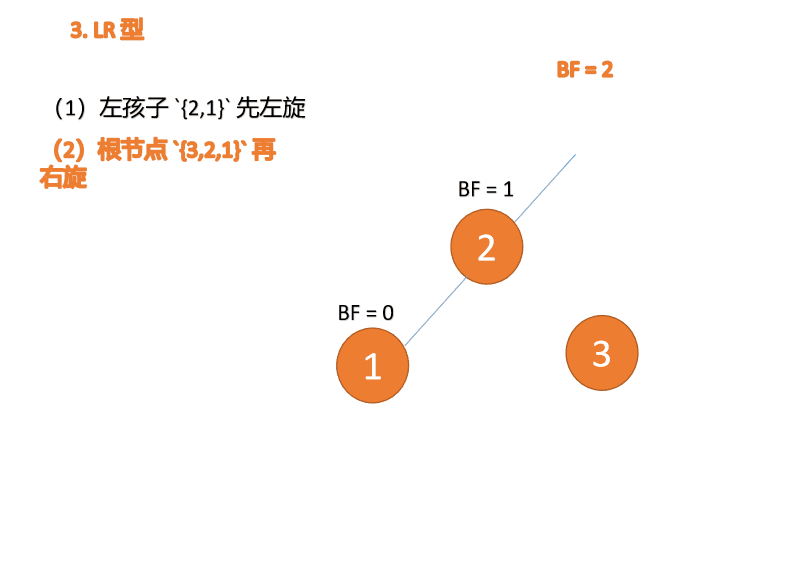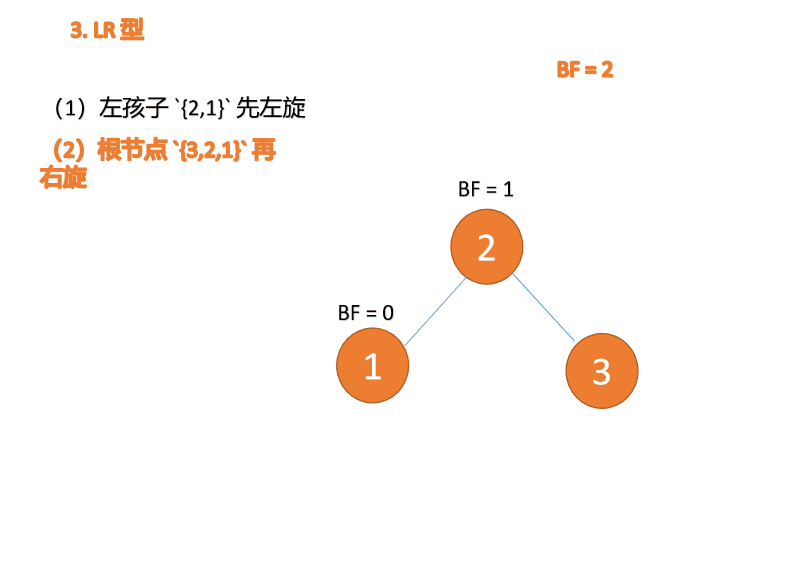
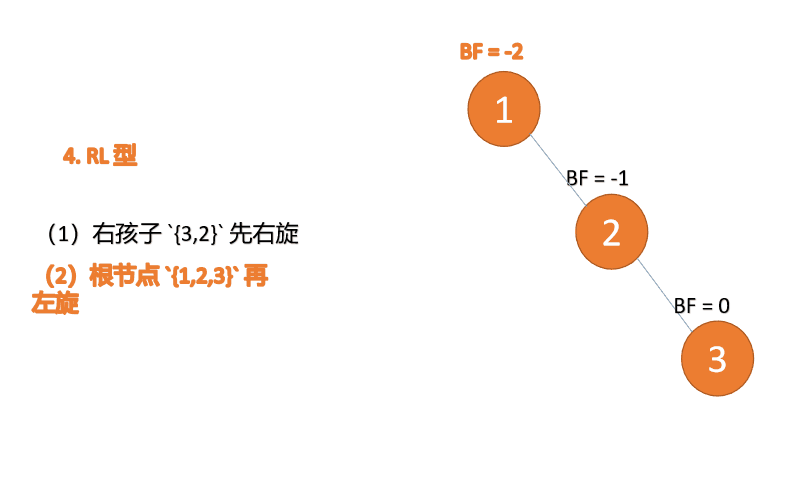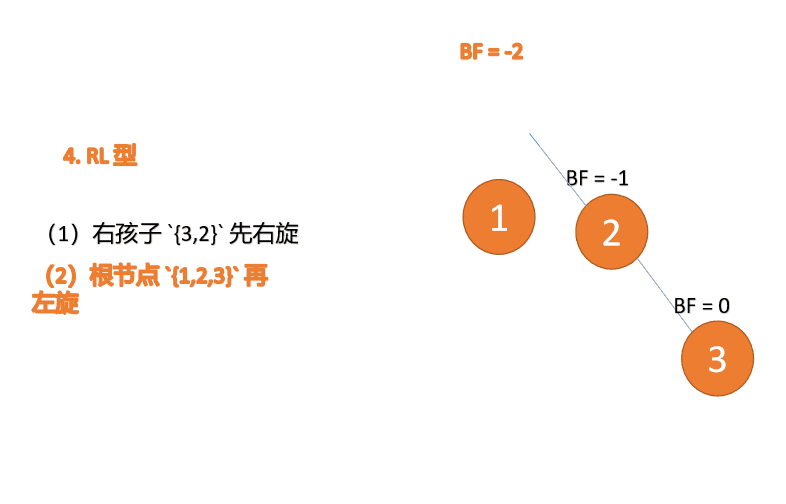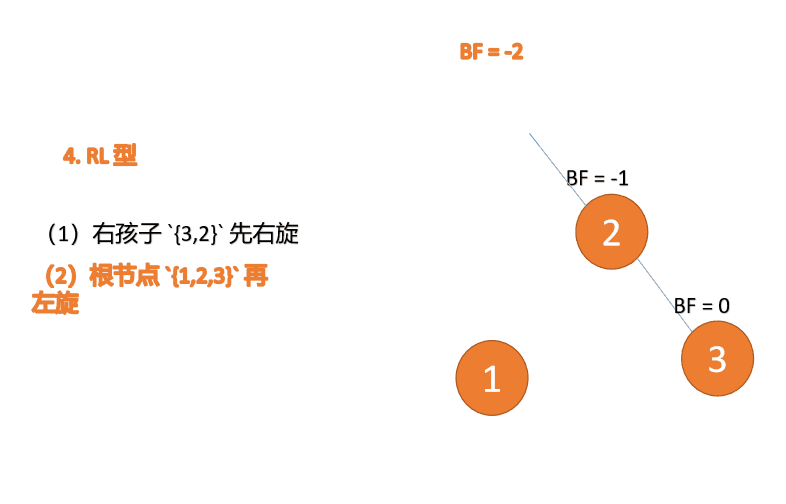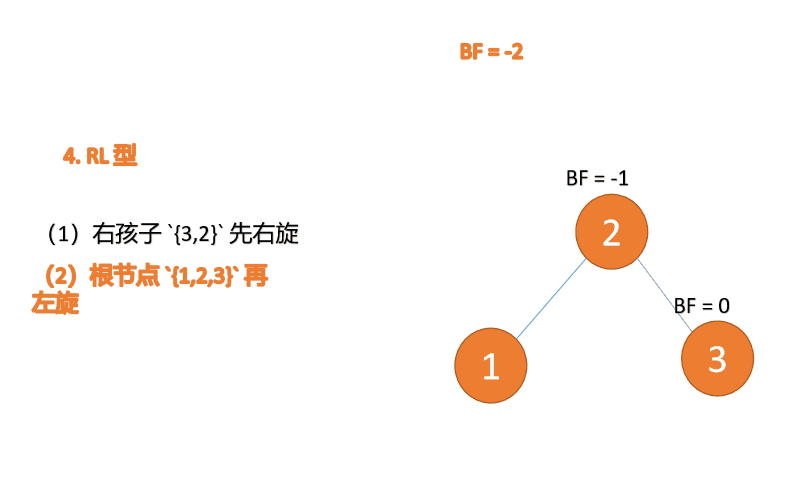
4.4 RL type
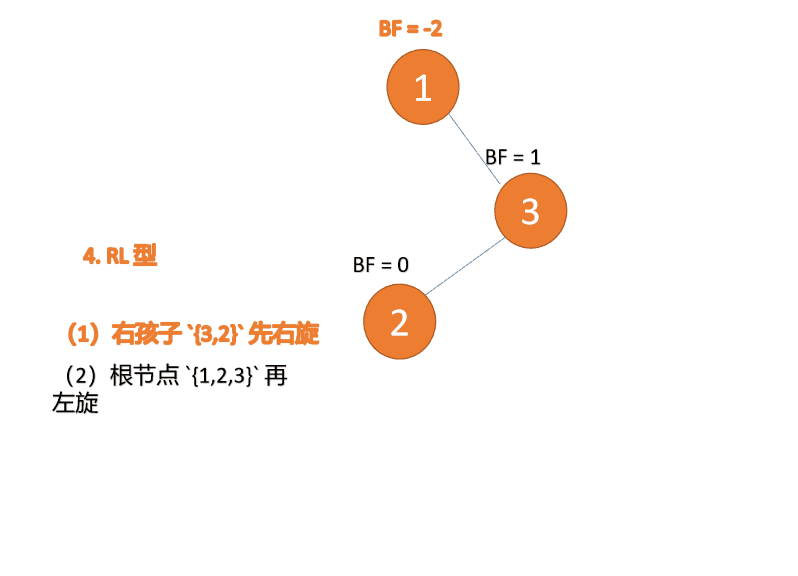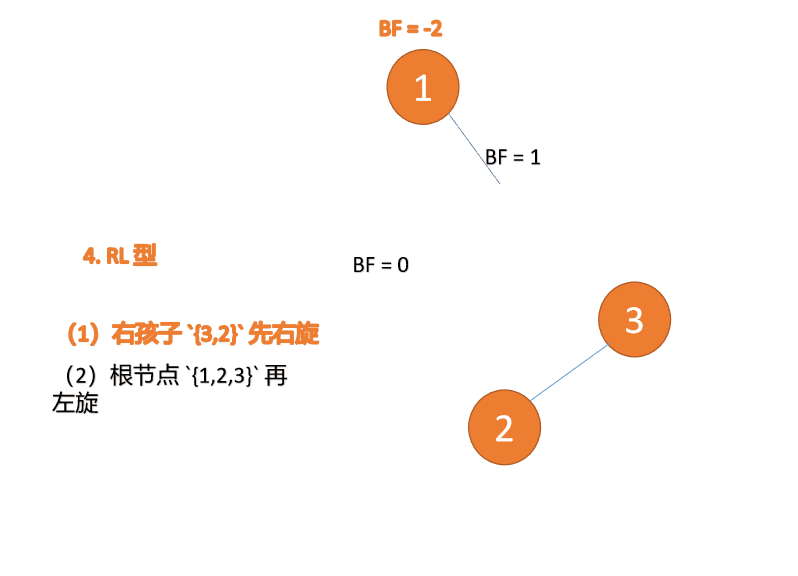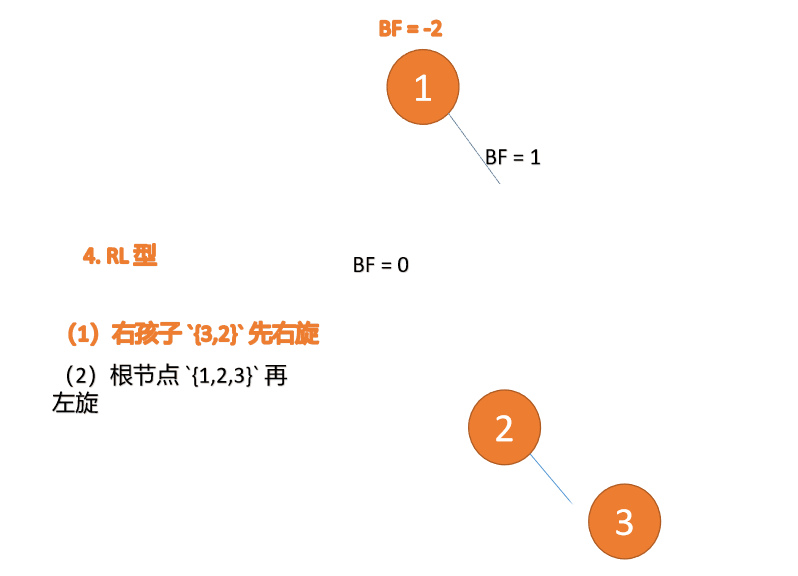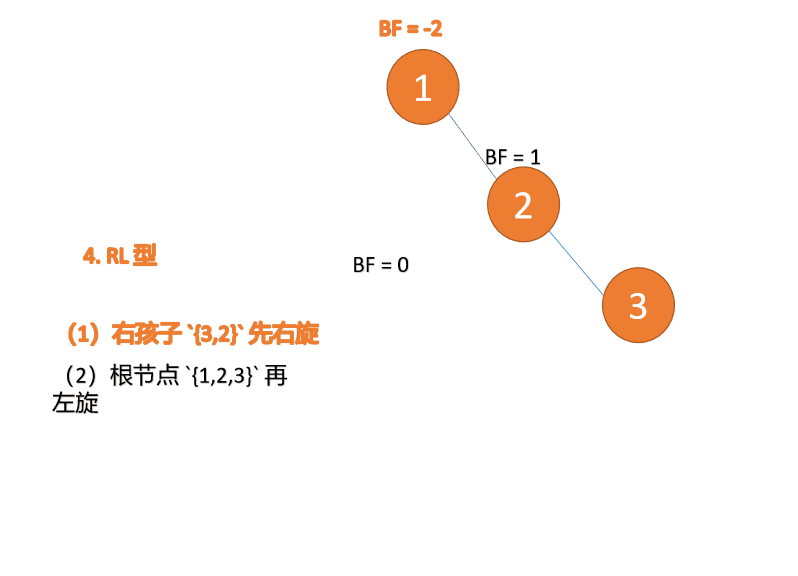
Third node 「1」 Inserted When ,BF(1)=-2 BF(3)=1RL Type imbalance , First 「 Right hand 」 Again 「 left-handed 」
（1） Minimum unbalanced subtree root node right subtree {3,2} First right
Right hand
- Old root node （ node 3） For the new root node （ node 2） The right subtree
- Of the new root node Right subtree （ If there is ） Is the left subtree of the old root node
（2） Minimum unbalanced subtree {1,2,3} Turn left again （L）
left-handed
- Old root node （ node 1） For the new root node （ node 2） The left subtree
- The left subtree of the new root node （ If there is ） Is the right subtree of the old root node
5. example
So let's start with {3,2,1,4,5,6,7,10,9,8} Practice just for example 4 There are two ways to insert
（1） Insert... In turn 3、2、1 Insert the third point 1 When BF(3)=2 BF(2)=1,LL Type imbalance .
For the minimum unbalanced tree {3,2,1} Conduct 「 Right hand 」
Right hand ：
- Old root node （ node 3） For the new root node （ node 2） The right subtree
- New root node （ node 2） The right subtree （ There is no right subtree ） Is the left subtree of the old root node
（2） Insert... In turn 4 ,5 Insert 5 A.m. BF(3) = -2 BF(4)=-1,RR Type imbalance
For the minimum unbalanced tree {3,4,5} Conduct 「 left-handed 」
left-handed ：
- Old root node （ node 3） For the new root node （ node 4） The left subtree
- New root node （ node 4） The left subtree （ There is no left subtree ） Is the right subtree of the old root node
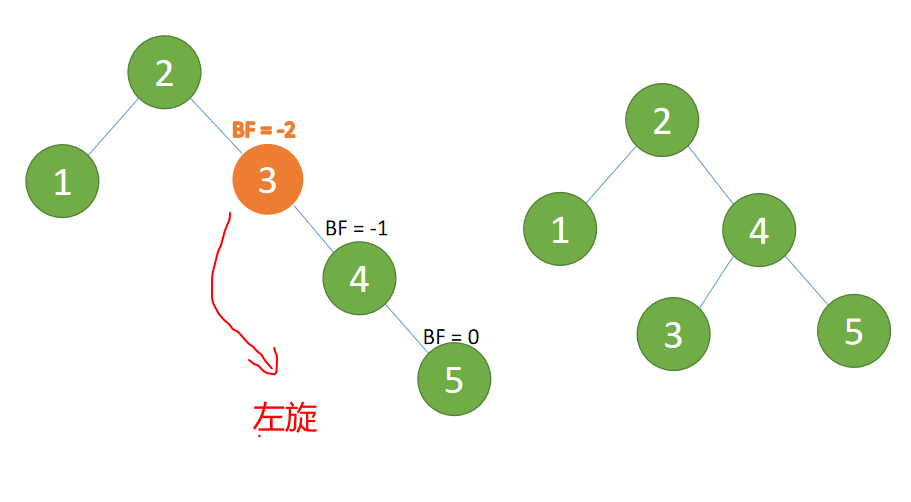
（3） Insert 4 ,5 Insert 5 A.m. BF(2)=-2 BF(4)=-1 ,RR Type imbalance For the minimum unbalanced tree 「 left-handed 」
left-handed ：
- Old root node （ node 2） For the new root node （ node 4） The left subtree
- New root node （ node 4） Of The left subtree （ node 3） Is the right subtree of the old root node
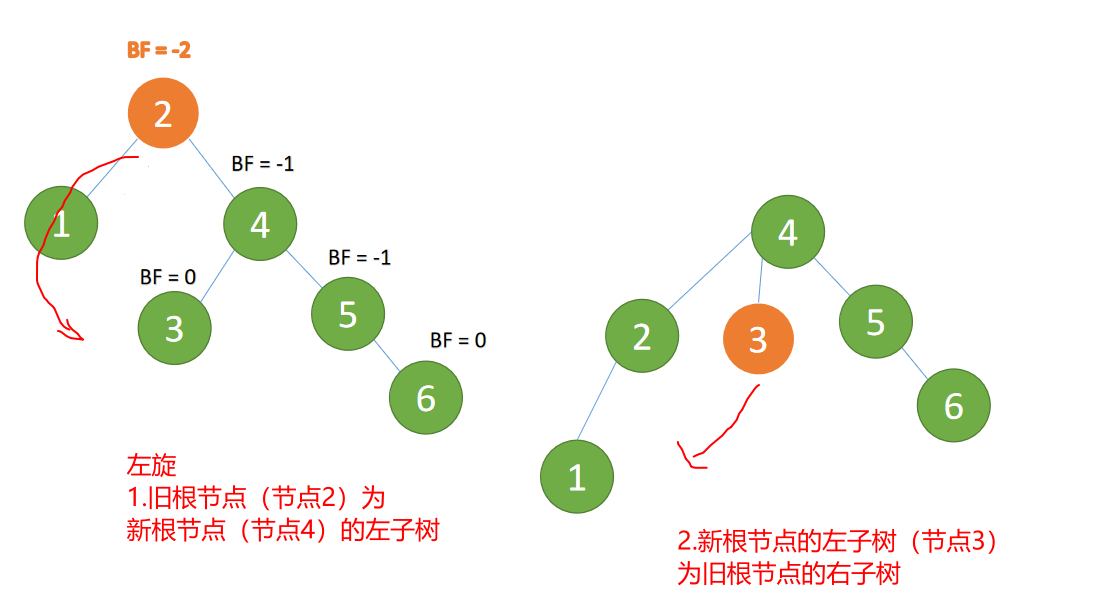
New root node （ node 4） The left subtree （ node 3） Is the right subtree of the old root node
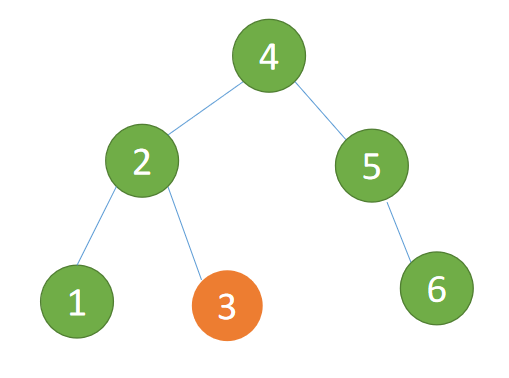
（4） Insert 7 Node time BF(5)=-2, BF(6)=-1 ,RR Type imbalance , For the minimum unbalanced tree Conduct 「 left-handed 」
left-handed ：
- Old root node （ node 5） For the new root node （ node 6） The left subtree
- The left subtree of the new root node （ Nothing here ） Is the right subtree of the old root node
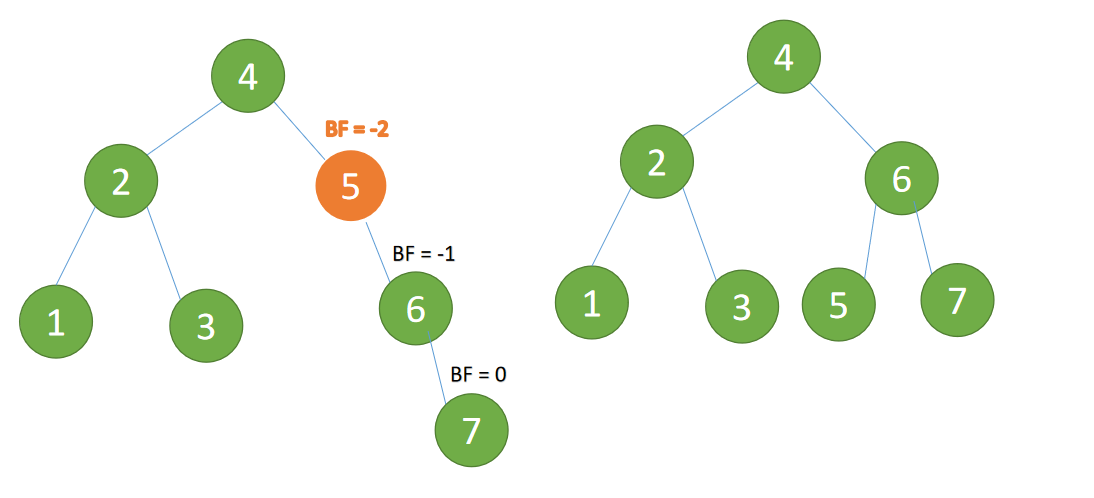
（5） Insert... In turn 10 ,9 . Insert 9 A.m. BF(10) = 1,BF(7) = -2 ,RL Type imbalance , Right first 「 Right hand 」 Again 「 left-handed 」
Right subtree first 「 Right hand 」
The right subtree of the minimum unbalanced subtree
{10,9}First right ：
- Old root node （ node 10） For the new root node （ node 9） The right subtree
- New root node （ node 9） The right subtree （ There is no right subtree ） Is the left subtree of the old root node
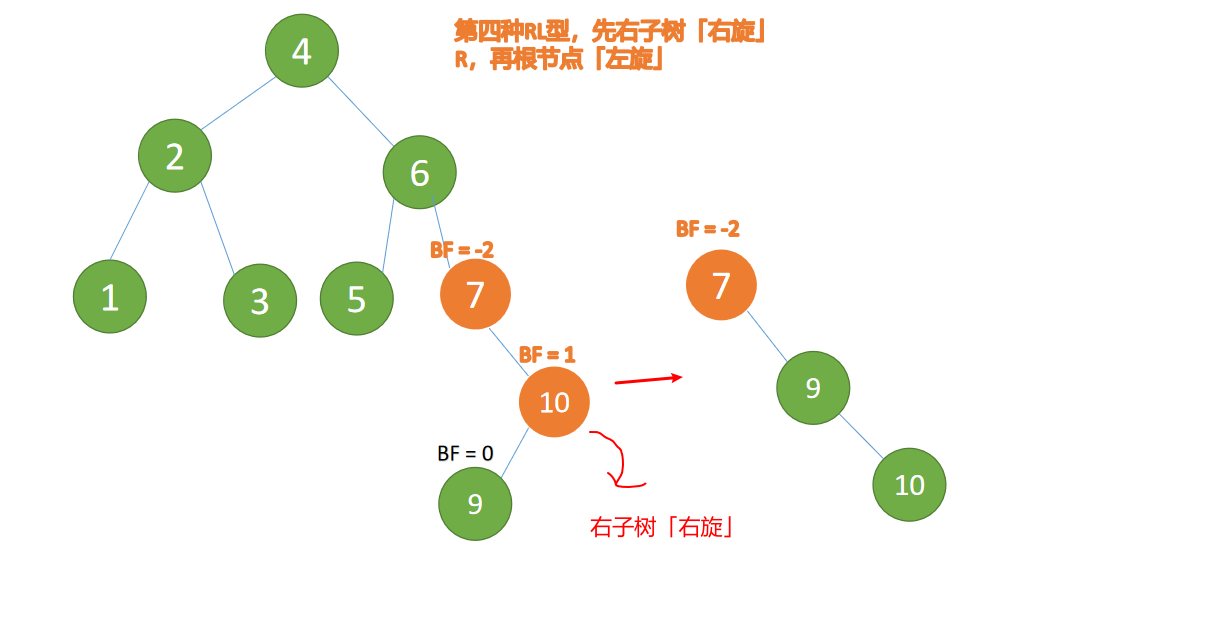
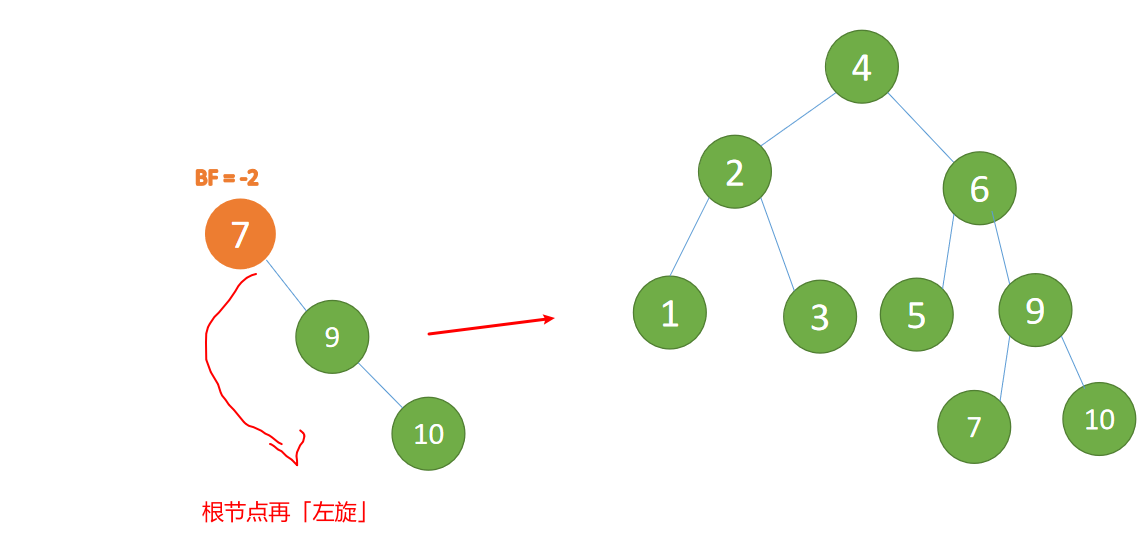
The minimum unbalanced subtree is then left-handed ：
- Old root node （ node 7） For the new root node （ node 9） The left subtree
- New root node （ node 9） The left subtree （ There is no left subtree ） Is the right subtree of the old root node
（6） Finally, insert the node 8 ,BF(6)=-2 BF(9)=1,RL Type imbalance , First 「 Right hand 」 Again 「 left-handed 」
The right subtree of the minimum unbalanced subtree {9,7,10,8} First 「 Right hand 」
Right hand ：
- Old root node （ node 9
{9,10}） For the new root node （ node 7） The right subtree - New root node （ node 7） The right subtree （ Here is node 8） For the old root node （ node 9） The left subtree
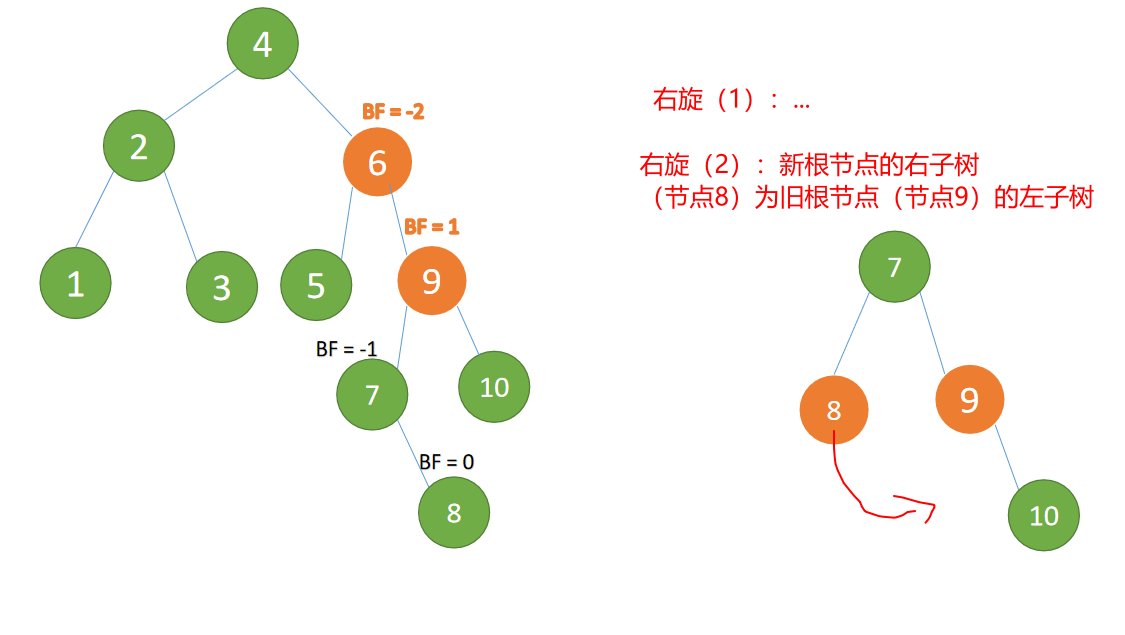
Minimum unbalanced subtree {6,5,7,9,8,10} Again 「 left-handed 」
left-handed ：
- Old root node （ node 6
{6,5}） For the new root node （ node 7） The left subtree - The left subtree of the new root node （ Nothing here ） Is the right subtree of the old root node
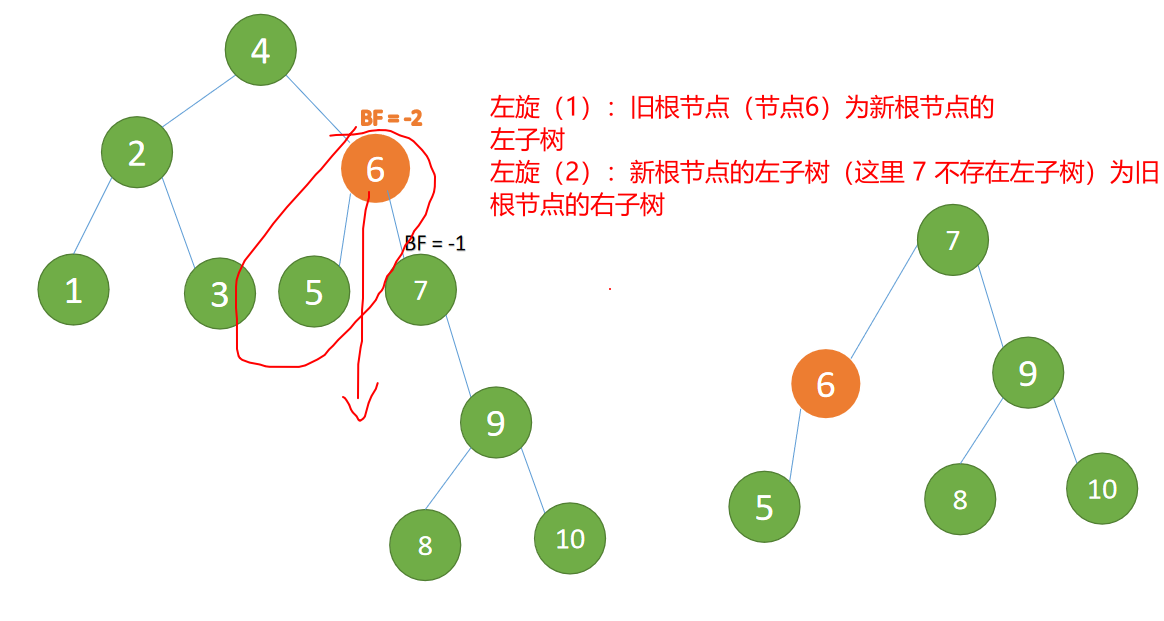
Left rotation end
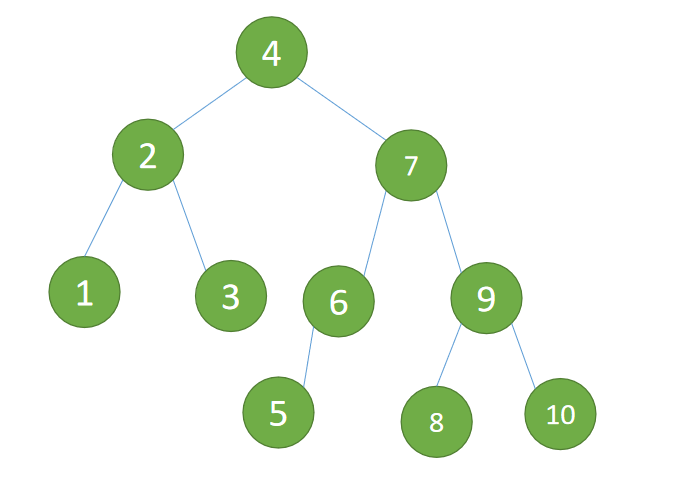
Program end
6. Code implementation
6.1 Define the node
public class AVLNode {
/** data **/
public int data;
/** Relative height **/
public int height;
/** Parent node **/
public AVLNode parent;
/** The left subtree **/
public AVLNode left;
/** Right subtree **/
public AVLNode right;
public AVLNode(int data) {
this.data = data;
this.height = 1;
}
}
6.2 Calculate the height
The node height is equal to the maximum height of the left subtree and the right subtree + 1
/** Through the height of subtree Calculate the height **/
private int calcHeight(AVLNode root) {
if (root.left == null && root.right == null) {
return 1;
}
else if (root.right == null) {
return root.left.height + 1;
} else if (root.left == null) {
return root.right.height + 1;
}else {
return root.left.height > root.right.height ? root.left.height + 1 : root.right.height + 1;
}
}
6.3 Calculation BF
BF（ Balance factor ） The value of is ： Height of left subtree - Height of right subtree
private int calcBF(AVLNode root) {
if (root == null){
return 0;
}
else if (root.left == null && root.right == null) {
return 0;
}
else if (root.right == null) {
return root.left.height ;
} else if (root.left == null) {
return - root.right.height;
}else {
return root.left.height - root.right.height;
}
}
6.4 rotate
2 Kind of 「 rotate 」 The way ：
- left-handed
- The old root node is the left subtree of the new root node
- The left subtree of the new root node （ If there is ） Is the right subtree of the old root node
- Right hand ：
- The old root node is the right subtree of the new root node
- The right subtree of the new root node （ If there is ） Is the left subtree of the old root node
Focus on understanding ： After rotation, you need to refresh the height
Height changes only ： oldRoot and newRoot
But the height of their subtrees is constant （ It's critical ）
We can use them Calculate the height of subtrees
Using constant factors to calculate changing factors is a good idea
public AVLNode leftRotate(AVLNode root) {
AVLNode oldRoot = root;
AVLNode newRoot = root.right;
AVLNode parent = root.parent;
//1.newRoot Replace oldRoot Location
if (null != parent ) {
if (oldRoot.parent.data > oldRoot.data) {
parent.left = newRoot;
}else {
parent.right = newRoot;
}
}
newRoot.parent = parent;
//2. Reassemble oldRoot ( take newRoot The left subtree to oldRoot The right subtree )
oldRoot.right = newRoot.left;
if (newRoot.left != null) {
newRoot.left.parent = oldRoot;
}
//3. oldRoot by newRoot The left subtree
newRoot.left = oldRoot;
oldRoot.parent = newRoot;
// Refresh height
oldRoot.height = calcHeight(oldRoot);
newRoot.height = calcHeight(newRoot);
return newRoot;
}
public AVLNode rightRotate(AVLNode root) {
AVLNode oldRoot = root;
AVLNode newRoot = root.left;
AVLNode parent = root.parent;
//1.newRoot Replace oldRoot Location
if (null != parent ) {
if (oldRoot.parent.data > oldRoot.data) {
parent.left = newRoot;
}else {
parent.right = newRoot;
}
}
newRoot.parent = parent;
//2. Reassemble oldRoot ( take newRoot The right subtree to oldRoot The left subtree )
oldRoot.left = newRoot.right;
if (newRoot.right != null) {
newRoot.right.parent = oldRoot;
}
//3. oldRoot by newRoot The left subtree
newRoot.right = oldRoot;
oldRoot.parent = newRoot;
// Refresh height
oldRoot.height = calcHeight(oldRoot);
newRoot.height = calcHeight(newRoot);
return newRoot;
}
6.5 Insert （ Master code ）
The insert
- Recursively insert new nodes
- Refresh height
- Rotate and refresh the height again
public class ALVTree {
AVLNode root;
public void insert(int data) {
if (null == this.root) {
this.root = new AVLNode(data);
return;
}
this.root = insert(this.root, data);
}
public AVLNode insert(AVLNode root, int data) {
// Insert the left subtree
if (data < root.data) {
if (null == root.left) {
root.left = new AVLNode(data);
root.left.parent = root;
}else {
insert(root.left,data);
}
}
// Insert right subtree
else if (data > root.data) {
if (null == root.right) {
root.right = new AVLNode(data);
root.right.parent = root;
} else {
insert(root.right,data);
}
}
// Refresh height
root.height = calcHeight(root);
// rotate
//1. LL type Right rotation
if (calcBF(root) == 2){
//2. LR type First left rotation
if (calcBF(root.left) == -1) {
root.left = leftRotate(root.left);
}
root = rightRotate(root);
}
//3. RR type Left rotation
if (calcBF(root) == -2){
//4. RL type First right rotation
if (calcBF(root.right)== 1) {
root.right = rightRotate(root.right);
}
root = leftRotate(root);
}
return root;
}
public AVLNode leftRotate(AVLNode root) {
AVLNode oldRoot = root;
AVLNode newRoot = root.right;
AVLNode parent = root.parent;
//1.newRoot Replace oldRoot Location
if (null != parent ) {
if (oldRoot.parent.data > oldRoot.data) {
parent.left = newRoot;
}else {
parent.right = newRoot;
}
}
newRoot.parent = parent;
//2. Reassemble oldRoot ( take newRoot The left subtree to oldRoot The right subtree )
oldRoot.right = newRoot.left;
if (newRoot.left != null) {
newRoot.left.parent = oldRoot;
}
//3. oldRoot by newRoot The left subtree
newRoot.left = oldRoot;
oldRoot.parent = newRoot;
// Refresh height
oldRoot.height = calcHeight(oldRoot);
newRoot.height = calcHeight(newRoot);
return newRoot;
}
public AVLNode rightRotate(AVLNode root) {
AVLNode oldRoot = root;
AVLNode newRoot = root.left;
AVLNode parent = root.parent;
//1.newRoot Replace oldRoot Location
if (null != parent ) {
if (oldRoot.parent.data > oldRoot.data) {
parent.left = newRoot;
}else {
parent.right = newRoot;
}
}
newRoot.parent = parent;
//2. Reassemble oldRoot ( take newRoot The right subtree to oldRoot The left subtree )
oldRoot.left = newRoot.right;
if (newRoot.right != null) {
newRoot.right.parent = oldRoot;
}
//3. oldRoot by newRoot The left subtree
newRoot.right = oldRoot;
oldRoot.parent = newRoot;
// Refresh height
oldRoot.height = calcHeight(oldRoot);
newRoot.height = calcHeight(newRoot);
return newRoot;
}
/** Through the height of subtree Calculate the height **/
private int calcHeight(AVLNode root) {
if (root.left == null && root.right == null) {
return 1;
}
else if (root.right == null) {
return root.left.height + 1;
} else if (root.left == null) {
return root.right.height + 1;
}else {
return root.left.height > root.right.height ? root.left.height + 1 : root.right.height + 1;
}
}
private int calcBF(AVLNode root) {
if (root == null){
return 0;
}
else if (root.left == null && root.right == null) {
return 0;
}
else if (root.right == null) {
return root.left.height ;
} else if (root.left == null) {
return - root.right.height;
}else {
return root.left.height - root.right.height;
}
}
}
test
public static void main(String[] args) {
ALVTree tree = new ALVTree();
tree.insert(3);
tree.insert(2);
tree.insert(1);
tree.insert(4);
tree.insert(5);
tree.insert(6);
tree.insert(7);
tree.insert(10);
tree.insert(9);
tree.insert(8);
// Traverse the output
innerTraverse(tree.root);
}
private static void innerTraverse(AVLNode root) {
if (root == null) {
return;
}
innerTraverse(root.left);
System.out.println(root.data + " height:"+root.height);
innerTraverse(root.right);
}
Output
1 height:1
2 height:2
3 height:1
4 height:4
5 height:1
6 height:2
7 height:3
8 height:1
9 height:2
10 height:1
边栏推荐
- 【RTKLIB 2.4.3 b34 】版本更新简介一
- [算法] 剑指offer2 golang 面试题12：左右两边子数组的和相等
- [算法] 剑指offer2 golang 面试题5：单词长度的最大乘积
- [Clickhouse kernel principle graphic explanation] about the collaborative work of partitioning, indexing, marking and compressed data
- Halcon knowledge: gray_ Tophat transform and bottom cap transform
- Liste des boucles de l'interface graphique de défaillance
- [Yu Yue education] guide business reference materials of Wuxi Vocational and Technical College of Commerce
- NRF24L01 troubleshooting
- Containers and Devops: container based Devops delivery pipeline
- KF UD分解之UD分解基础篇【1】
猜你喜欢
KF UD分解之UD分解基础篇【1】
idea中导包方法
![[算法] 剑指offer2 golang 面试题9：乘积小于k的子数组](/img/65/fc3fb5a217a3b44f506b695af53e2c.png)
[算法] 剑指offer2 golang 面试题9：乘积小于k的子数组
MySQL shutdown is slow
FairyGUI人物状态弹窗
Excel导入，导出功能实现
The master of double non planning left the real estate company and became a programmer with an annual salary of 25W. There are too many life choices at the age of 25
Latex learning
Office prompts that your license is not genuine pop-up box solution
![[Nodejs] 20. Koa2 onion ring model ----- code demonstration](/img/a8/a4390238685903b63bb036206f8dcb.jpg)
[Nodejs] 20. Koa2 onion ring model ----- code demonstration
随机推荐
Unity3D摄像机，键盘控制前后左右上下移动，鼠标控制旋转、放缩
[offer18] delete the node of the linked list
NRF24L01 troubleshooting
NovAtel 板卡OEM617D配置步骤记录
What is the maximum length of MySQL varchar field
堆排序【手写小根堆】
MySQL shutdown is slow
There is no red exclamation mark after SVN update
[899] ordered queue
dosbox第一次使用
Fairygui loop list
341. Flatten nested list iterator
idea问题记录
Office提示您的许可证不是正版弹框解决
雇佣收银员【差分约束】
闇の連鎖（LCA+树上差分）
（5） Introduction to R language bioinformatics -- ORF and sequence analysis
FairyGUI循環列錶
FairyGUI复选框与进度条的组合使用
[算法] 劍指offer2 golang 面試題2：二進制加法