当前位置:网站首页>nn. Exploration and experiment of batchnorm2d principle
nn. Exploration and experiment of batchnorm2d principle
2022-07-04 11:42:00 【Andy Dennis】
Preface
In the morning, I was asked by my classmates for batch norm Principle , Because I only used torch.nn.BatchNorm2d The stage of , Just know it's right channel Dimension can be normalized in batches , But it is not clear about the specific implementation , So I did the experiment . First look at it. torch Example , Then write a handwritten version of the calculation code .
bn Every element after y i y_i yi It can be simply written as
y i = x i − x ˉ σ 2 + ϵ y_i = \frac{x_i-\bar{x}}{\sqrt{\sigma^{2}} + \epsilon} yi=σ2+ϵxi−xˉ
among , x i x_i xi Is a previous element , x ˉ \bar{x} xˉ yes channel The mean on the dimension , σ \sigma σ yes channel The standard deviation of dimensions , ϵ \epsilon ϵ Is a coefficient factor , ( A bit like Laplacian smoothing , Prevent denominator from being 0?but I’m not sure), The default is 1 0 − 5 10^{-5} 10−5, A very small number .
torch The way
# encoding:utf-8
import torch
import torch.nn as nn
input = torch.tensor([[[[1, 1],
[1, 2]],
[[-1, 1],
[0, 1]]],
[[[0, -1],
[2, 2]],
[[0, -1],
[3, 1]]]]).float()
# num_features - num_features from an expected input of size:batch_size*num_features*height*width
# eps:default:1e-5 ( In the formula is the value added to the denominator for numerical stability )
# momentum: Momentum parameter , be used for running_mean and running_var Calculated value ,default:0.1
# affine The parameter is set to True Express weight and bias Will be used , However, there is no back propagation in this example , So it doesn't matter whether you add it or not
m = nn.BatchNorm2d(2, affine=False)
output = m(input)
# print('input:\n', input)
print('m.weight:\n', m.weight)
print('m.bias:', m.bias)
print('output:\n', output)
print('output:', output.size())
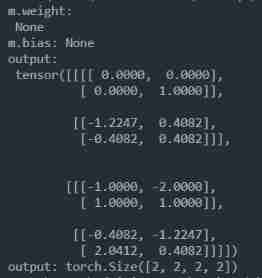
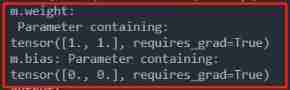
The point here is , It doesn't matter affine Set to True, In this example, the results are the same , We can see by looking at the weight , weight whole 1, Then multiply and return to the original number , bias by 0, Then it will be the original number after adding . There is no back propagation , So the weight will not change .
hand writing
We have nothing but channel Outside the channel , Other dimensions are flattened , Then calculate the mean and variance , Use the calculated mean and variance to operate the original data .
# encoding:utf-8
from matplotlib.pyplot import axis
import torch
import torch.nn as nn
input = torch.tensor([[[[1, 1],
[1, 2]],
[[-1, 1],
[0, 1]]],
[[[0, -1],
[2, 2]],
[[0, -1],
[3, 1]]]]).float()
# [B, C, H, W]
N, c_num, h, w = input.shape
print(input.shape)
x = input.transpose(0, 1).flatten(1)
# print(x)
c_mean = x.mean(dim=1)
print('c_mean:', c_mean)
c_std = torch.tensor(x.numpy().std(axis=1)) # Standard deviation formula , torch N-1, numpy N
print('c_std^2:', c_std ** 2)
# # Expand dimensions , And copy the elements , Convenient for the following batch operation
c_mean = c_mean.reshape(1, 2, 1, 1).repeat(N, 1, h, w)
c_std = c_std.reshape(1, 2, 1, 1).repeat(N, 1, h, w)
# # print(c_mean)
# # print(c_std)
eps = 1e-5
output = (input - c_mean) / (c_std ** 2 + eps) ** 0.5
print(output)
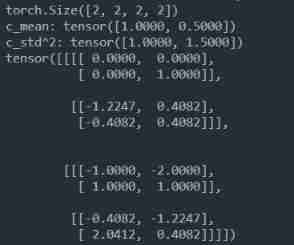
There's a little bit of caution here , pytorch and numpy The formula for calculating the standard deviation of is different , That's why I changed my code to numpy Do it again . But it's reasonable pytorch It should be possible to pass a parameter or something to change the calculation method .
numpy:
s t d = 1 N ∑ i = 1 N ( x i − x ˉ ) 2 std = \sqrt{\frac{1}{N}\sum^{N}_{i=1}(x_i-\bar{x})^2 } std=N1i=1∑N(xi−xˉ)2
torch:
s t d = 1 N − 1 ∑ i = 1 N ( x i − x ˉ ) 2 std = \sqrt{\frac{1}{N-1}\sum^{N}_{i=1}(x_i-\bar{x})^2 } std=N−11i=1∑N(xi−xˉ)2
边栏推荐
- LxC shared directory addition and deletion
- First knowledge of spark - 7000 words +15 diagrams, and learn the basic knowledge of spark
- regular expression
- If function in SQL
- [ES6] template string: `string`, a new symbol in es2015
- Configure SSH key to realize login free
- [Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 10
- [Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 16
- DDS-YYDS
- [Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 7
猜你喜欢
Force buckle 142 Circular linked list II

OSI seven layer reference model
![[solve the error of this pointing in the applet] SetData of undefined](/img/19/c34008fbbe1175baac2ab69eb26e05.jpg)
[solve the error of this pointing in the applet] SetData of undefined
![[Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 20](/img/d5/4bce239b522696b5312b1346336b5f.jpg)
[Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 20
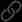
SQL greatest() function instance detailed example
Ternsort model integration summary
Experiment 7. IPv6
![Entitas learning [iv] other common knowledge points](/img/1c/f899f4600fef07ce39189e16afc44a.jpg)
Entitas learning [iv] other common knowledge points
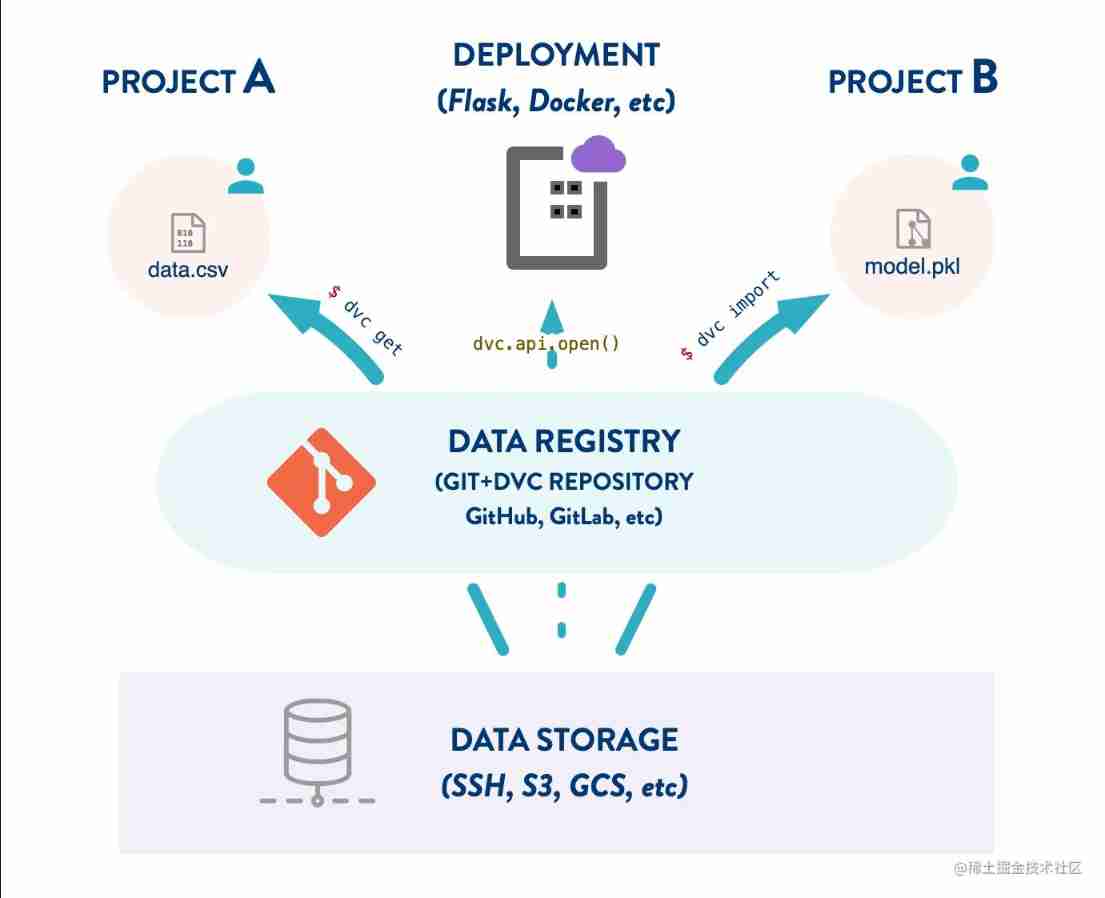
DVC use case (VI): Data Registry
Reptile learning 3 (winter vacation learning)
随机推荐
(2021-08-20) web crawler learning 2
Iptables cause heartbeat brain fissure
试题库管理系统–数据库设计[通俗易懂]
[Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 6
Some tips on learning database
三立期货安全么?期货开户怎么开?目前期货手续费怎么降低?
Summary of Shanghai Jiaotong University postgraduate entrance examination module -- cryptography
(August 9, 2021) example exercise of air quality index calculation (I)
本地Mysql忘记密码的修改方法(windows)[通俗易懂]
Decrypt the advantages of low code and unlock efficient application development
C language memory layout
Customized version of cacti host template
Common built-in modules
[Yunju entrepreneurial foundation notes] Chapter II entrepreneur test 7
Cacti主机模板之定制版
Review of week 278 of leetcode II
JD home programmers delete databases and run away. Talk about binlog, the killer of MySQL data backup
Summary of collection: (to be updated)
Login operation (for user name and password)
Reptile learning 4 winter vacation series (3)