当前位置:网站首页>rtklib单点定位spp使用抗差估计遇到的问题及解决
rtklib单点定位spp使用抗差估计遇到的问题及解决
2022-07-06 09:18:00 【Proletarians】
问题描述
在spp中应用抗差估计时,在计算观测值验后残差v的协方差阵的时候,出现了问题,Qvv对角元出现了负值。
首先,我怀疑是自己代码出了问题,紧接着就是调试,在vs中调试矩阵这方面真的是让人头大。
其次,我将spp中的系数矩阵H、常数矩阵l、协方差阵Qxx、参数向量dx打印出来了,在matlab验证对比。
1、matlab中打印上述的矩阵
>> H=[ 0.497179 -0.767231 0.405178 1.000000 0.000000 0.000000 0.000000;
0.954274 0.112689 -0.276879 1.000000 0.000000 0.000000 0.000000;
0.387339 -0.481553 -0.786178 1.000000 0.000000 0.000000 0.000000;
-0.580737 -0.519400 -0.626872 1.000000 0.000000 0.000000 0.000000;
-0.287620 -0.601084 -0.745636 1.000000 0.000000 0.000000 0.000000;
0.394442 -0.847597 -0.354957 1.000000 0.000000 0.000000 0.000000;
0.479621 -0.224119 -0.848371 1.000000 0.000000 0.000000 0.000000;
-0.266211 -0.887121 0.377026 1.000000 0.000000 0.000000 0.000000;
0.000000 0.000000 0.000000 0.000000 1.000000 0.000000 0.000000;
0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 0.000000;
0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000];
>> Q=[ 1.444742 -1.205538 -0.559907 -1.256723 0.000000 0.000000 0.000000;
-1.205538 4.239855 1.510516 3.308947 0.000000 0.000000 0.000000;
-0.559907 1.510516 1.847995 1.891790 0.000000 0.000000 0.000000;
-1.256723 3.308947 1.891790 3.215663 0.000000 0.000000 0.000000;
0.000000 0.000000 0.000000 0.000000 0.010000 0.000000 0.000000;
0.000000 0.000000 0.000000 0.000000 0.000000 0.010000 0.000000;
0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.010000];
>> dx=[ 0.000009
-0.000020
-0.000022
-0.000041
0.000000
0.000000
0.000000];
>> l=[0.123075
0.433912
0.828791
0.067140
0.026320
-0.289038
-0.862615
-0.198928
0.000000
0.000000
0.000000];
>> H'
ans =
Columns 1 through 8
0.497179000000000 0.954274000000000 0.387339000000000 -0.580737000000000 -0.287620000000000 0.394442000000000 0.479621000000000 -0.266211000000000
-0.767231000000000 0.112689000000000 -0.481553000000000 -0.519400000000000 -0.601084000000000 -0.847597000000000 -0.224119000000000 -0.887121000000000
0.405178000000000 -0.276879000000000 -0.786178000000000 -0.626872000000000 -0.745636000000000 -0.354957000000000 -0.848371000000000 0.377026000000000
1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
Columns 9 through 11
0 0 0
0 0 0
0 0 0
0 0 0
1.000000000000000 0 0
0 1.000000000000000 0
0 0 1.000000000000000
>> H*Q*H'
ans =
Columns 1 through 8
1.332860500714645 0.645546014871716 -0.098580562413659 -0.064031507548390 -0.165752578512155 0.396295832699334 -0.141008818175153 1.168889713304825
0.645546014871717 1.968804844653495 0.053246247795955 -0.005468449432181 -0.265950607478022 -0.319534503408733 0.574091433817809 0.243277031690377
-0.098580562413659 0.053246247795955 0.357273653443425 -0.021840446651663 0.164659427109121 0.283415207166032 0.318871615198842 -0.284958778729781
-0.064031507548390 -0.005468449432181 -0.021840446651663 1.072132904685670 0.641476084869937 -0.226446903091478 0.079281778351138 0.679077103029250
-0.165752578512155 -0.265950607478023 0.164659427109121 0.641476084869937 0.515321629013082 0.067397424711531 0.125308500906703 0.247806596987045
0.396295832699334 -0.319534503408734 0.283415207166032 -0.226446903091478 0.067397424711531 0.647339251042735 0.015423699735895 0.151774558340723
-0.141008818175153 0.574091433817809 0.318871615198843 0.079281778351138 0.125308500906704 0.015423699735896 0.481685375510297 -0.331346855770643
1.168889713304826 0.243277031690377 -0.284958778729780 0.679077103029250 0.247806596987045 0.151774558340723 -0.331346855770643 1.674731658216493
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
Columns 9 through 11
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0.010000000000000 0 0
0 0.010000000000000 0
0 0 0.010000000000000
>>
2、在vs中打印上述矩阵
2.1 打印Q_矩阵
我在vs中计算HQH’时出了问题,代码如下:
printf("**********************\n");
Q_ = mat(nv, nv);
matmul("TN", nv, NX, NX, 1.0, H_, Q, 0.0, Q);
matmul("NN", nv, nv, NX, 1.0, Q, H_, 0.0, Q);
printmat(Q, nv, nv, "Q");
其中,matmul是矩阵相乘的函数,T表示转置,N表示不转置;H_是系数矩阵,未加权的系数矩阵,是rescode函数直接返回的H的拷贝,Q是lsq的返回值,Q_表示HQH’,那么按照上述代码得出的打印结果如下图所示:
对角元有负值,并且不是对角矩阵,很明显就是错了嘛,哈哈哈
2.2、打印系数矩阵H
在rescode函数中H是按照[-e1 -e2 -e3 1.0 0.0 0.0 0.0]这样来放在数组或矩阵中的,这样就是nv * NX个元素了,我是按mat定义的NX * nv来打印,再按照nv * NX来打印,结果如下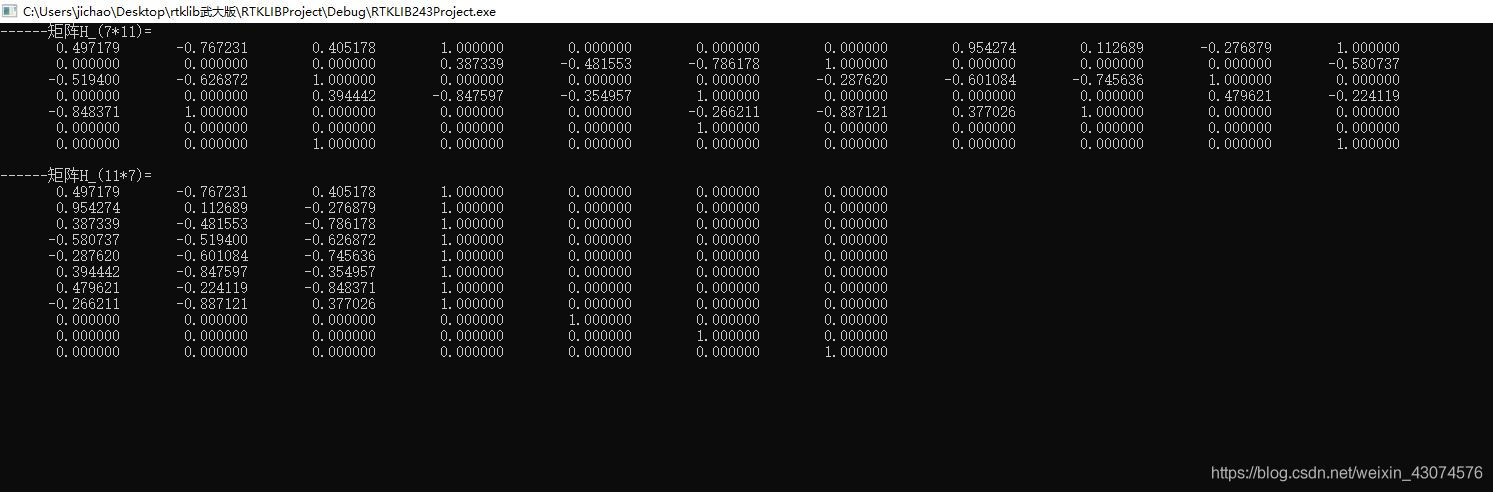
系数矩阵H说是NX * nv,打印的结果显示内部数据排列应该是上述第二个打印矩阵转置的形式,也就是说H的形式其实就是matlab中H’的形式
2.3、打印H‘ * H
为了验证2.2中上述的结论,就对H’ * H的结果进行打印,如下图所示: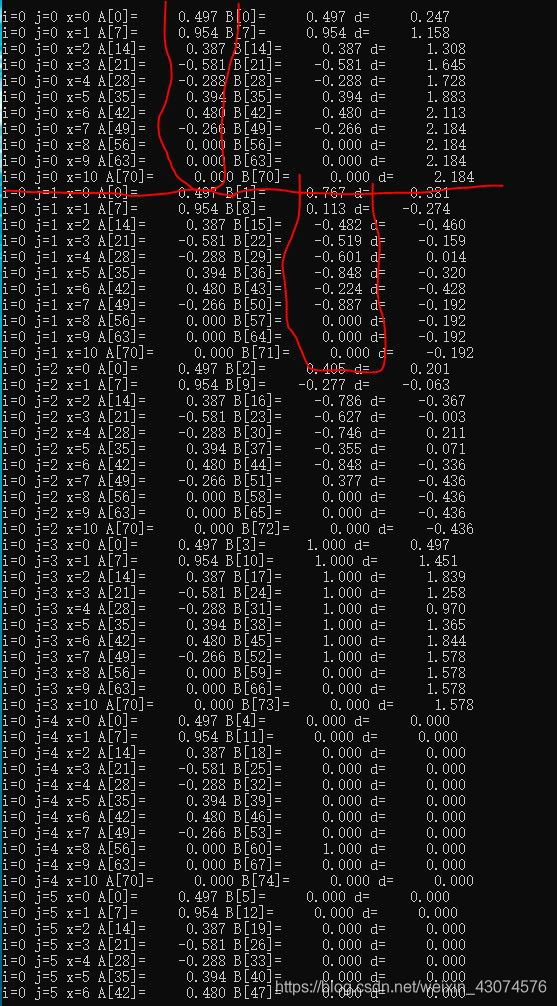
2.4、对2.1中矩阵相乘运算修改验证
先对H和单位矩阵相乘,计算出来H‘,再进行H‘QH运算
// 3、根据协方差传播定律可知,Qvv=Qll-B*Q*B',Q=(B'PB)^-1
// lsq: n<m,n=NX m=nv
// matmul("NN",n,1,m,1.0,A,y,0.0,Ay); /* Ay=A*y */
// matmul("NT", n, n, m, 1.0, A, A, 0.0, Q); /* Q=A*A' */
printf("**********************\n");
Q_ = mat(nv, nv);
double *eyeI;
double *tH;
eyeI = mat(NX, NX);
tH = mat(nv, NX);
for (j = 0; j < NX;j++)
{
for (k = 0; k < NX;k++)
{
eyeI[j + k*NX] = (j==k)?1.0:0.0;
}
}
matmul("TN", nv, NX, NX, 1.0, H_, eyeI, 0.0, tH); /* 求转置矩阵H' */
printmat(tH, NX, nv, "tH");// 打印转置矩阵
double *Q1,*Q2;
Q1 = mat(nv, NX);
Q2 = mat(nv, nv);
matmul("NN", nv, NX, NX, 1.0, tH, Q, 0.0, Q1);
matmul("NN", nv, nv, NX, 1.0, Q1, H_, 0.0, Q_);
printmat(Q_, nv, nv, "Q_");
打印结果如下: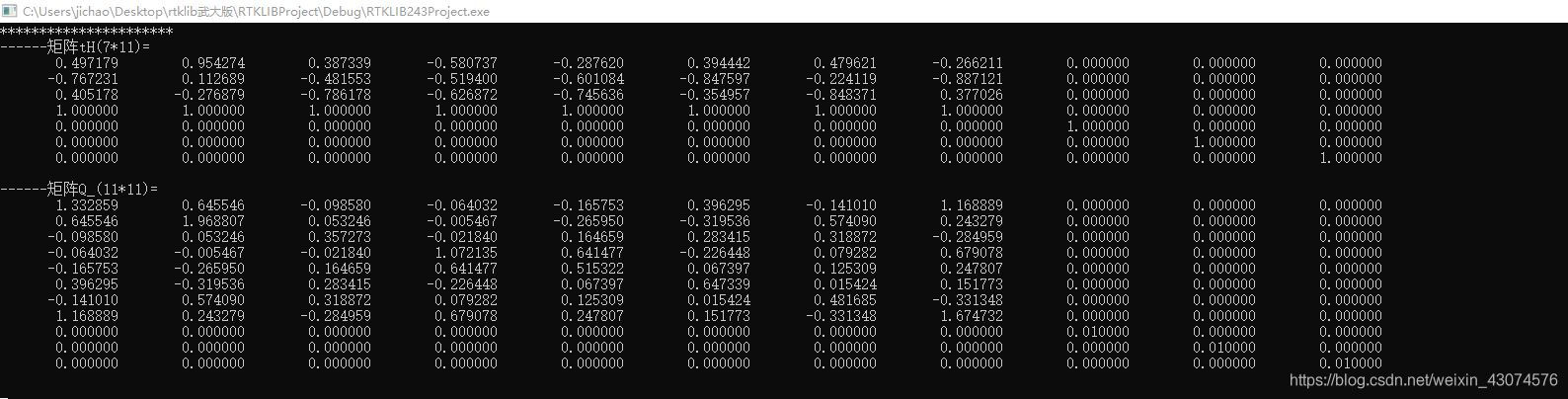
其实这个tH就是Matlab中的H的转置形式,再次用调试手段验证了rtklib的矩阵是按第一列、第二列。。。第n列的形式填充矩阵的,跟我们平时自己写代码习惯不一样。打印结果和Matlab一致了。
抗差代码
spp中加入抗差的代码也写完了,测试验证了下,确实加了抗差的rms和std要比不加抗差的小,等我把代码的注释加好,会把 测试数据+代码+结果图 放出来,大家交流一下。
边栏推荐
- Unity3D摄像机,键盘控制前后左右上下移动,鼠标控制旋转、放缩
- [offer29] sorted circular linked list
- 基于rtklib源码进行片上移植的思路分享
- Unity3D制作注册登录界面,并实现场景跳转
- JS Title: input array, exchange the largest with the first element, exchange the smallest with the last element, and output array.
- Idea problem record
- Detailed explanation of truncate usage
- Mysql database index
- Fairygui joystick
- [899]有序队列
猜你喜欢
FairyGUI簡單背包的制作
FairyGUI复选框与进度条的组合使用
SVN更新后不出现红色感叹号
程序设计大作业:教务管理系统(C语言)

C programming exercise
Unity3D基础入门之粒子系统(属性介绍+火焰粒子系统案例制作)

Derivation of logistic regression theory
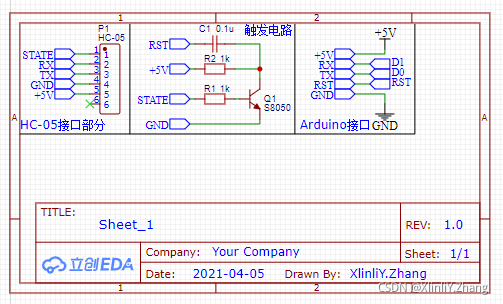
Single chip Bluetooth wireless burning
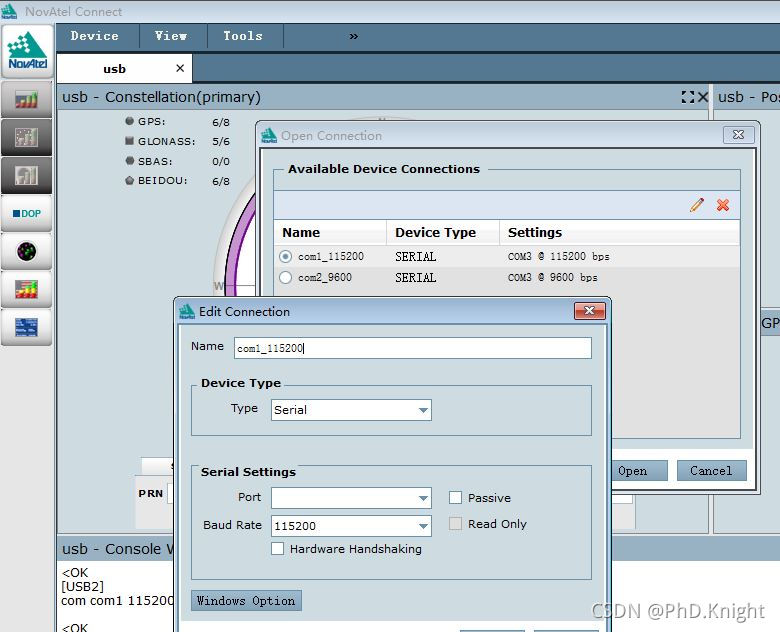
NovAtel 板卡OEM617D配置步骤记录
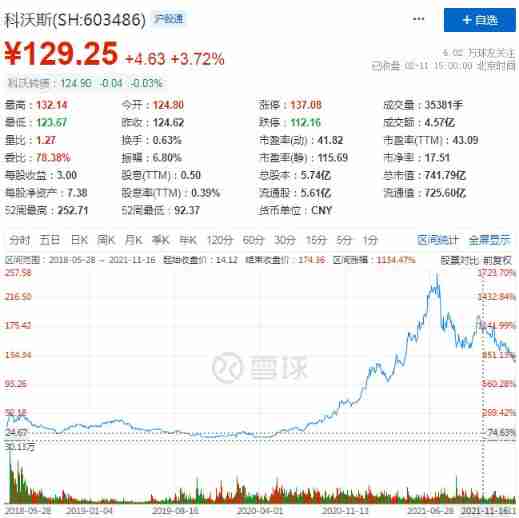
The service robots that have been hyped by capital and the Winter Olympics are not just a flash in the pan
随机推荐
音乐播放(Toggle && PlayerPrefs)
[offer9] implement queues with two stacks
PT OSC deadlock analysis
The service robots that have been hyped by capital and the Winter Olympics are not just a flash in the pan
PR 2021 quick start tutorial, first understanding the Premiere Pro working interface
FairyGUI增益BUFF數值改變的顯示
Mysql database index
Acwing-116 pilot brother
2022.2.12 resumption
ESP8266连接onenet(旧版MQTT方式)
(3) Introduction to bioinformatics of R language - function, data Frame, simple DNA reading and analysis
Affichage du changement de valeur du Buff de gain de l'interface graphique de défaillance
Expected value (EV)
[899] ordered queue
Unity3D制作注册登录界面,并实现场景跳转
程序设计大作业:教务管理系统(C语言)
(三)R语言的生物信息学入门——Function, data.frame, 简单DNA读取与分析
[leetcode622]设计循环队列
341. Flatten nested list iterator
MySQL error warning: a long semaphore wait