2.非线性回归

代码运行平台为jupyter-notebook，文章中的代码块，也是按照jupyter-notebook中的划分顺序进行书写的，运行文章代码，直接分单元粘入到jupyter-notebook即可。

1.导入第三方库

import keras
import numpy as np
import matplotlib.pyplot as plt
# Sequential 按顺序构成的模型
from keras.models import Sequential
# Dense 全连接层
from keras.layers import Dense,Activation
from tensorflow.keras.optimizers import SGD

2.随机生成数据集

# 使用numpy生成200个随机点
# 在-0.5~0.5生成200个点
x_data = np.linspace(-0.5,0.5,200)
noise = np.random.normal(0,0.02,x_data.shape)
# y = x^2 + noise
y_data = np.square(x_data) + noise

# 显示随机点
plt.scatter(x_data,y_data)
plt.show()

运行结果：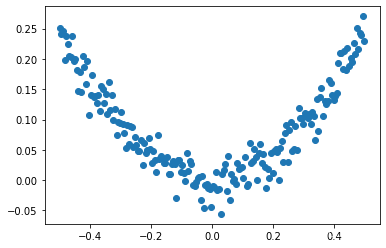

3.非线性回归

# 构建一个顺序模型
model = Sequential()
# 按shift+tab可以显示参数

# 1-10-1 输入一个神经层，10个隐藏层，输出一个神经层
model.add(Dense(units=10,input_dim=1))

# 添加激活函数 激活函数默认情况下是线性的，但是我们是非线性回归，所以要对激活函数进行修改
# 添加激活函数 方式一：直接添加activation参数
# model.add(Dense(units=10,input_dim=1,activation="relu"))

# 添加激活函数 方式二：直接添加Activation激活层
model.add(Activation("tanh"))

model.add(Dense(units=1,input_dim=10))
# model.add(Dense(units=1,input_dim=10,activation="relu"))
model.add(Activation("tanh"))

# 定义优化算法 提高学习率可以降低迭代次数
sgd = SGD(lr=0.3)

# sgd:Stochastic gradient descent , 随机梯度下降法 默认的sgd学习率表较小 所以需要的迭代次数就比较多 消耗的时间也就更多
# mse:Mean Squared Error , 均方误差
model.compile(optimizer=sgd,loss='mse')


# 训练3001个批次
for step in range(3001):
    # 每次训练一个批次
    cost = model.train_on_batch(x_data,y_data)
    # 每500个batch打印一次cost
    if step%500==0:
        print("cost:",cost)

# 打印权值和批次值
W,b = model.layers[0].get_weights()
print("W:",W)
print("b:",b)

# x_data输入网络中得到预测值
y_pred = model.predict(x_data)

# 显示随机点
plt.scatter(x_data,y_data)
# 显示预测结果
plt.plot(x_data,y_pred,"r-",lw=3)
plt.show()

运行结果：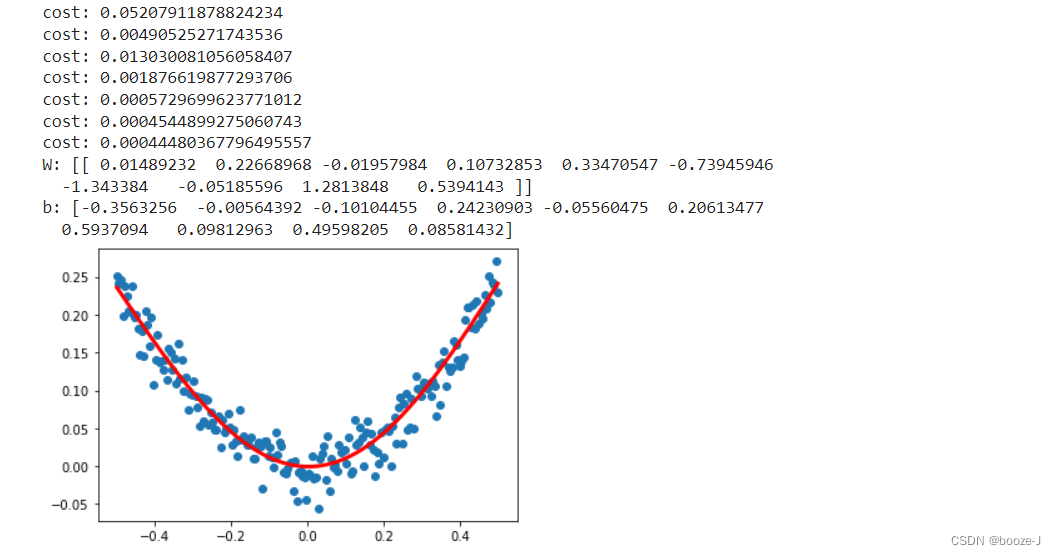

注意

• 1.进行非线性回归的要注意修改激活函数，因为激活函数默认情况下是线性的。
• 2.默认的sgd学习率表较小 所以需要的迭代次数就比较多 消耗的时间也就更多，所以可以自定义sgd学习率进行学习。
• 3.整体上代码和线性回归的代码非常类似，只是修改了一下数据集，网络模型，激活函数，以及优化器。