当前位置:网站首页>C - Divisors of the Divisors of An Integer Gym - 102040C
C - Divisors of the Divisors of An Integer Gym - 102040C
2022-07-05 13:59:00 【beyond+myself】
题目链接
题意:就是求n!中因子的因子的个数
题解:
①:n!中某个因子的个数就是n/x的累加。
证明:其实就是每次褪一层,即每次除去能除于1个3的,依次两个3的,三个3的个数,最终也就能得到3的个数,这里没必要
整除,因为是阶乘,所以即使不能整除,也可以被比数组中较小的数整除。
我们举一个例子:
1234567 我们找最终得到的2的个数,第一次 我们发现 2 4 6 可以整除,整除后变成了 1 2 3 随之7/2=3,ans+=3,随之2依然可以整除,然后变成了1,随之3/2=1,后面都不能整除了,所以我们可以找到这个规律。
②:假设可以把阶乘得到的结果化成类似于2 ^ a * 3 ^ b * 5 ^ c这样的,我们可以得出结果——是(a+1)*(a+2) / 2 * (b+1) * (b+2) / 2 *(c+1) * (c+2) / 2;
证明:我们将他们写成以上那种形式后,其实因子就很好求了,如果让求因子的个数,这个题到此为止,但是题目要求的是因子的因子的个数,所以我们这里还不能完,因子的因子的个数就是——我们单求
一个质数单元,例如是:3 ^ 0 的因子个数是1个,3 ^ 1 是两个,3 ^ a的因子个数 ( 3 ^ 0 ~ 3 ^ a)共a+1个 所以 我们把他们加起来是(a+1) * (a+2)/2 这样 在将所有的乘起来即可,也就是类似于排列组合的情况数,当所有的数都选择0次方时,也就是1。
下面是AC代码:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
const int N=1e6+10,mod=1e7+7;
int prime[N];
bool st[N];
int cnt[N];
int cou;
void is_prime(int n)
{
int i,j;
for(i=2;i<=n;i++)
{
if(!st[i])
{
prime[cou++]=i;
for(j=i+i;j<=n;j+=i) st[j]=true;
}
}
}
signed main()
{
is_prime(1e6);
int n;
while(cin>>n&&n)
{
memset(cnt,0,sizeof(cnt));
for(int i=0;prime[i]<=n;i++)
{
cnt[i]=0;
int tmp=n;
while(tmp)
{
cnt[i]+=tmp/prime[i];
tmp/=prime[i];
}
}
int ans=1;
for(int i=0;prime[i]<=n;i++)
{
if(cnt[i]>0)
{
ans=(ans%mod*((cnt[i]+1)*(cnt[i]+2)/2)%mod)%mod;
}
}
printf("%lld\n",ans);
}
return 0;
}
边栏推荐
- Linked list (simple)
- Ueditor + PHP enables Alibaba cloud OSS upload
- Attack and defense world crypto WP
- 深拷贝真难
- VC开发非MFC程序内存泄漏跟踪代码
- Idea remote debugging agent
- Primary code audit [no dolls (modification)] assessment
- 如何将 DevSecOps 引入企业?
- Can graduate students not learn English? As long as the score of postgraduate entrance examination English or CET-6 is high!
- 牛客网:拦截导弹
猜你喜欢

【华南理工大学】考研初试复试资料分享
These 18 websites can make your page background cool

Laravel framework operation error: no application encryption key has been specified
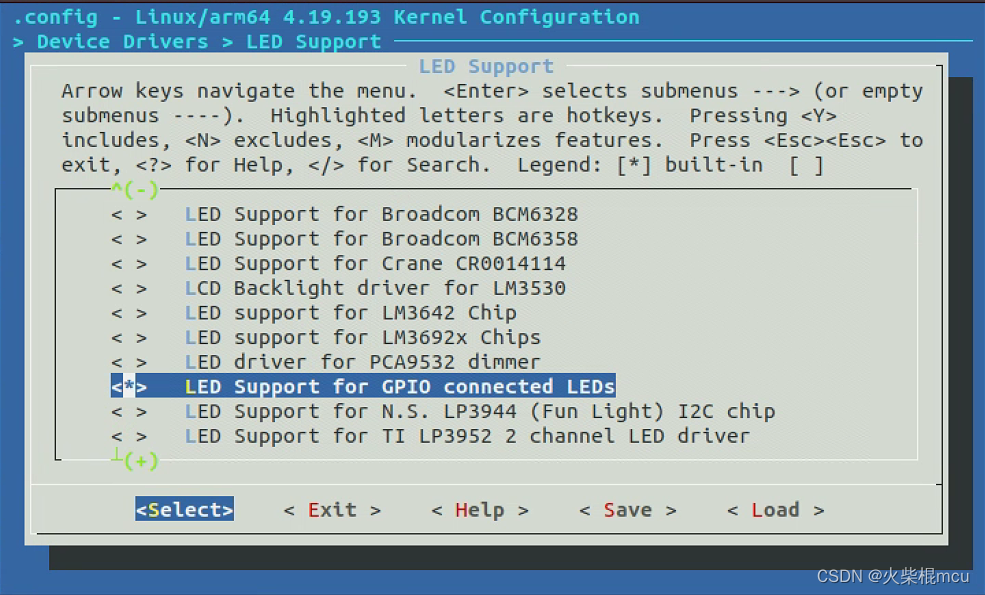
RK3566添加LED

Those things I didn't know until I took the postgraduate entrance examination
-Web direction attack and defense world
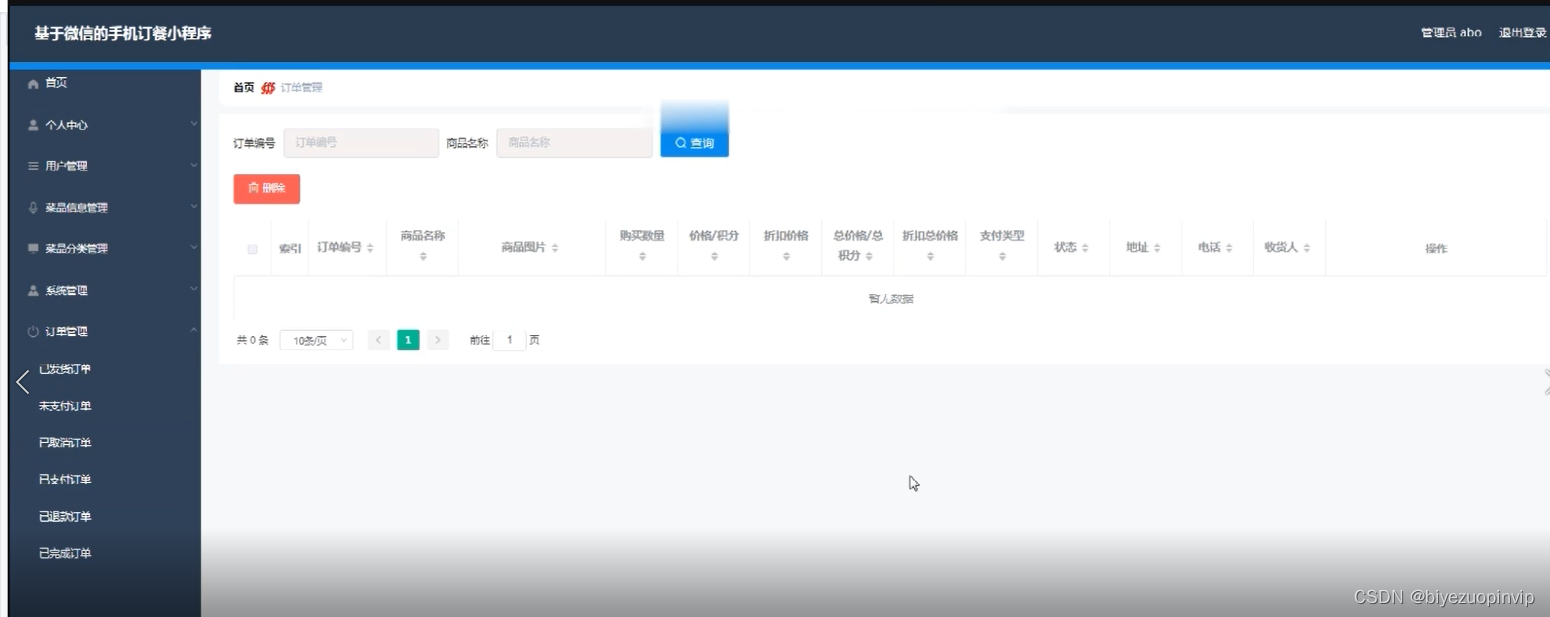
Ordering system based on wechat applet
What is the future development trend of neural network Internet of things
upload (1-6)

Laravel dompdf exports PDF, and the problem of Chinese garbled code is solved
随机推荐
JS takes key and value from an array object to form a new object
NFT value and white paper acquisition
锚点导航小demo
神经网络物联网未来现状和趋势及看法
uplad_ Labs first three levels
Zibll theme external chain redirection go page beautification tutorial
Financial one account Hong Kong listed: market value of 6.3 billion HK $Ye wangchun said to be Keeping true and true, long - term work
Idea remote debugging agent
Simple process of penetration test
Anchor navigation demo
Zhubo Huangyu: these spot gold investment skills are not really bad
Implementation process of WSDL and soap calls under PHP5
PHP basic syntax
Wechat app payment callback processing method PHP logging method, notes. 2020/5/26
Why do I support bat to dismantle "AI research institute"
04_solr7.3之solrJ7.3的使用
RK3566添加LED
Kafaka log collection
Xampp configuring multiple items
Request + BS4 crawl Netease cloud music popular comments