当前位置:网站首页>风控模型启用前的最后一道工序,80%的童鞋在这都踩坑
风控模型启用前的最后一道工序,80%的童鞋在这都踩坑
2022-07-05 10:16:00 【番茄风控】
评分卡模型,在信贷风控体系中是一种很常见的模型表现形式,不仅通过分数能够直观量化用户的综合风险程度,而且在实际业务中显示出通俗易懂的风控解释意义。
评分卡模型根据具体业务场景的差异,会区分不同的模型应用类型,例如贷前申请评分卡模型(A卡)、贷中行为评分卡模型(B卡)、贷后催收评分卡模型(C卡)、贷前反欺诈评分卡模型(F卡)等。这些常见类型的评分卡模型,虽然从模型开发数据、模型目标定义、模型应用实现等方面考虑,各自都有不同的属性特点,但从建模整个流程上分析,包括数据预处理、特征工程、模型训练等各个环节,建模节点的处理步骤都比较类似。同时,A、B、C、F卡等风控模型的最终分数,都是根据模型训练的预测概率转换而来,而这个评分逻辑转换的原理都是一致的。
针对信贷风控场景常见的评分卡模型,了解评分转换的原理机制以及应用特点,对于从事风控模型岗位的小伙伴来讲,是非常基础也是非常重要的一项内容,无论是在应聘模型岗位的面试环节,还是日常模型开发的工作情景,评分卡模型已经成为一个必要话题。因此,熟悉并掌握评分卡模型的分数转换原理,并深入理解评分应用的风控场景,显得非常有必要。此道工序也是模型工作中的最后一part,有不少在此踩坑的童鞋。基于此,本文将结合此业务背景,给大家重点介绍下评分卡模型的分数转换形式,共分为标准刻度评分卡和简单概率评分卡两种情况。
1、标准刻度评分卡
评分卡分数的本质是由概率转换而来,具体是通过一定的评分标尺来设定分值刻度,以坏好比率(odds)对数的线性表达式来定义分数,可以通过以下公式表示,其中odds=p/(1-p),以A卡实现场景说明,p为客户预测为违约的概率,1-p为客户预测为正常的概率。
Score=A-Bln(odds)
在以上公式中,A与B均为常数,可以很直观地理解,当用户的违约概率p值越高,那最终的分数越低,这样在业务中可以通过分数的高低,来量化评估用户风险程度的大小。因此,由模型的概率向评分的转换,在实际业务中有着非常重要的意义,简单概括为两个要点:一方面是将原始概率区间范围0~1,以分数形式进行放大,相比概率小数形式,评分整数更便于业务人员理解;另一方面是结合实际场景可以对分数区间大小进行指定,通过分数制定风控相关策略更为直观简洁。
在实际业务场景中,针对公式Score=A-Bln(odds),要得到最终分数Score,需要指定参数A和B,但这两个参数是很难解释期业务含义的。因此,我们经常会通过指定其他参数(基准坏好比odds、基准分base_score、odds翻倍分数pdo),来来推理出参数A和B的值,具体表示如下:
Score=A-Bln(odds)
Score-pdo-=A-Bln(2odds)
由以上两公式可以得到参数A和B的逻辑:
B=pdo/ln(2)
A=Score+Bln(odds)
现在我们结合场景需求与业务经验(没有绝对标准),假设当base_score为300时,对应odds为1:10,而pdo设为30(指odds翻倍为2:10时,分数500降低为270),然后将初设值带入以上公式,可以得到具体的A、B值。
B=30/ln(2)=43.28
A=300+43.28ln(1/10)=200.34
以上关于评分卡标准系数设定的过程,通过代码实现如下图1所示:

图1 评分卡标准设定
当得到参数A和B的具体值后,便可以根据评分卡公式Score=A-B*ln(p/(1-p)),很容易算出每个样本用户的最终分数,其中p值为响应概率(例如A卡模型的p值为预测违约概率),现通过以下图2样例数据进一步说明评分结果,其中score最终结果取整数表示。
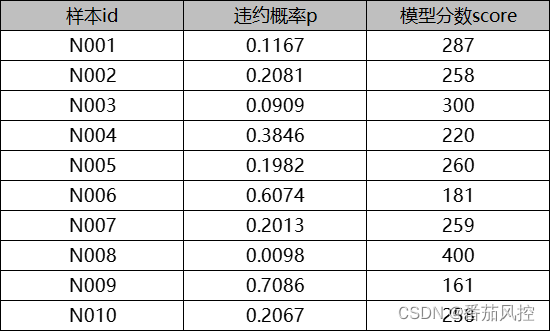
图2 标准刻度评分
由上图结果可以很直观了解到,模型预测的违约概率越高,对应的分数越低。其中id=N003的样本,模型分score=300恰好是我们前边设定的基础分数,那对应的odds=p/(1-p)=0.0909/(1-0.0909)=1:10,正是我们预先设定好的基准坏好比odds,这里也验证了前边设定好的评分标准。
以上标准评分转换的原理逻辑,是评分卡制定的核心思想,我们虽然在风控“外表”上看到的是模型分数,而实质体现的业务“内在”是客户违约概率,而中间构建关系的“纽带”则是样本坏好比odds。
2、简单概率评分卡
以上标准刻度评分卡的制定逻辑,是我们实际场景中最为常用的转换方式,此外还有一种较为简单的映射方式,就是将预测概率结果p值直接线性约束到我们希望的评分区间,这样也是有实际业务意义的,这里我们仍然选取前边图2的数据样例进行说明。假设我们设定模型评分范围为300~600,那么预测违约概率p=0与p=1分别对应评分600与300,这样通过线性关系,p值每增加0.0001,分数依次减少0.03分,反之亦然。根据这种概率与分数的线性转换关系,图2样本原始数据的最终分数结果如图3所示,其中score最终结果取整数表示。

图3 简单概率评分
针对以上两种评分转换方式,在实际场景应用中都有一定的风控价值与分析意义,二者进行比较,虽然简单概率评分的方式计算更为简单且便于理解,但是标准刻度评分在实际解释意义更强,同时也有利于针对业务情况进行调整。因此,在实际场景中,优先考虑采用标准刻度评分方式来构建评分模型。
3、评分卡应用场景
通过以上评分转换方式的介绍,我们熟悉了模型分数在实际业务中的风控价值,正因如此,评分卡模型在信贷很多场景中得到应用,包括获客、贷前、贷中、贷后等阶段,这对于信贷风控的精细化管理有着非常重要的意义,例如常见的A、B、C、F卡主要落地应用场景如下:
(1)贷前申请评分模型(A卡):违约风险预测、授信额度制定
(2)贷中行为评分模型(B卡):风险监测预警、产品额度调整
(3)贷后催收评分模型(C卡):还款能力预测、催收策略制定
(4)贷前反欺诈评分模型(F卡):申请欺诈预测
现以贷前风控场景为例,描述下A卡模型评分区间展示的重要指标,具体样例如图4所示。
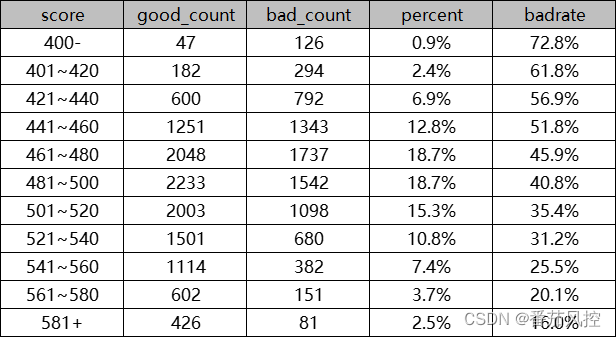
图4 模型评分指标
由上图可知,随着用户的申请评分score升高,对应区间的违约坏账率badrate逐渐降低,而且呈现出的单调性趋势越好,说明模型的区分性能越强。图4样例数据的响应坏账率badrate与模型分数score的变化关系,通过可视化图表展示如图5所示,可以更形象的体现出模型的业务解释意义。在实际业务场景中,根据选定的决策分数阈值制定模型策略进行应用,例如当申请用户的模型score<=440时则拒绝,具体阈值选取依据,需要结合样本整体坏账率与实际业务需求而定。
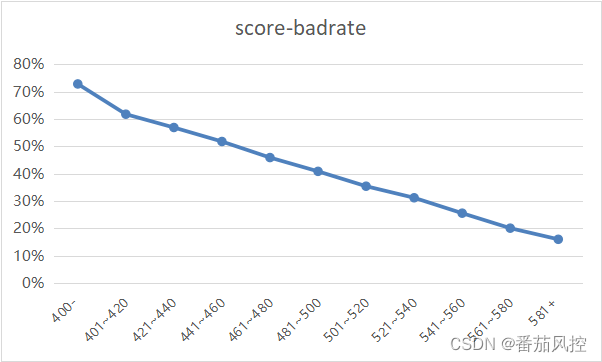
图5 模型评分趋势
4、模型评分展现
当我们开发完成评分卡模型后,无论是针对模型训练还是模型测试环节,必然会对模型评分的具体分布进行分析(如上图4所示),我们往往会将样本的评分划分为多个区间,然后来探究各个评分区间的样本频率、数量占比、坏账表现等,从而分析得到出评分卡模型的应用效果。这里我们需要注意的是,在划分模型评分区间时,一般是选取等距或等频两种方式,等距是保证各评分区间的分数间距相等,但样本数量不一定相等;而等频是保证各评分区间的样本数量相等,但分数间距不一定相等。在实际业务场景中,我们一般是采用评分等距的方式来划分评分区间,下面我们简要介绍下具体的优点。
图6与图7为评分卡模型分别采用评分等距、评分等频两种方式来展示的模型分布结果,每种方式都划分为10个评分区间bin。
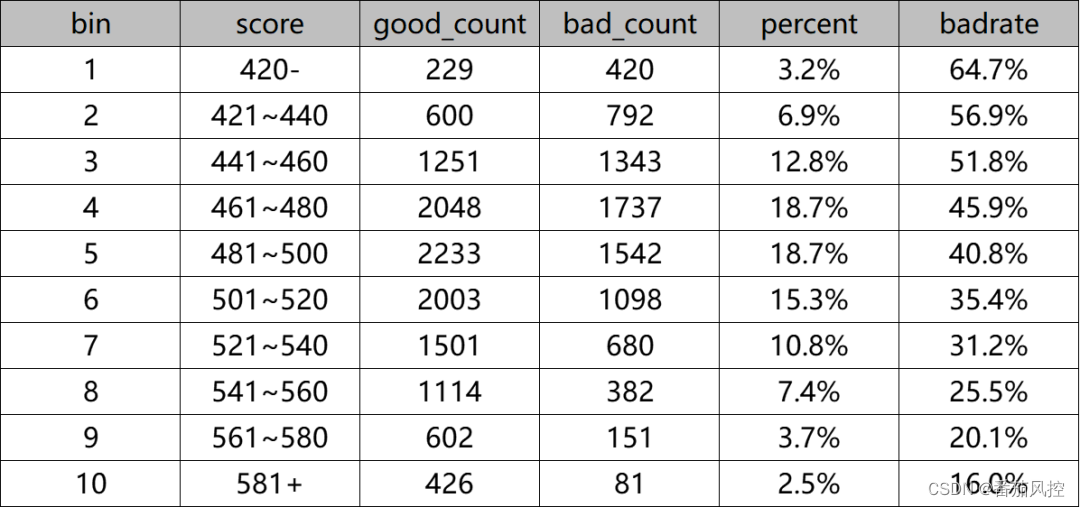
图6 模型评分等距区间
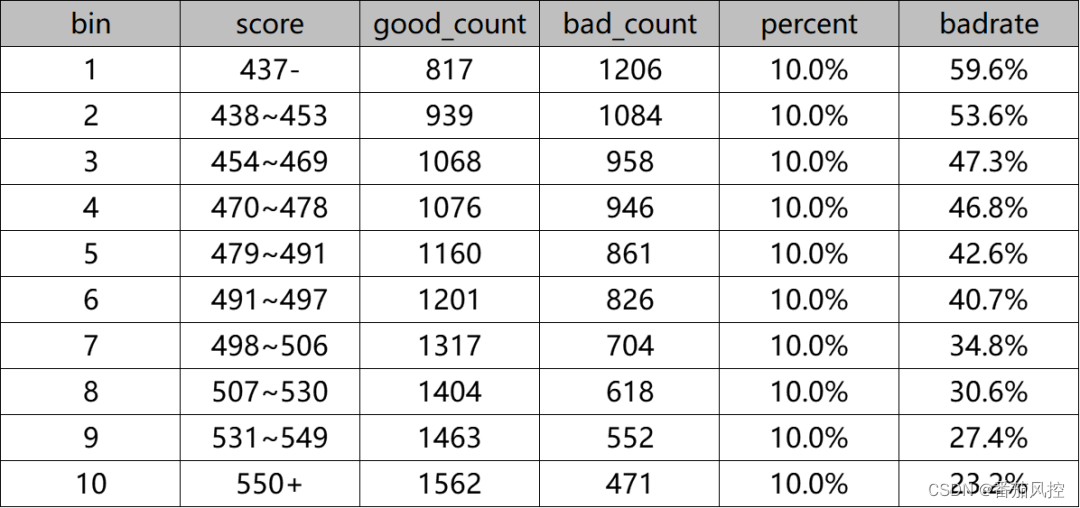
图7 模型评分等频区间
由上图结果可知,评分区间的等距或等频方式展示响应趋势是一致的,也就是样本坏账率badrate随着评分score升高而逐渐降低,这是模型具有较好区分度效果的本质决定的。但是,我们在进一步探究样本在模型各个分数段的占比分布时,显然图7等频方式的分布结果很难得到有效且合理的分析。一般情况下,评分卡模型如果训练效果较好,最终评分的样本群体分布往往会呈现出类似正态分布的形态,也就是两端分别对应的低分数段和高分数段的样本占比是最低的,这对于我们选择模型的决策阈值,或者对样本用户进行评级是非常有效的。图8为采用评分等距方式得到的各分数区间样本占比分布,可以很直观的了解到样本群体模型评分的集中与分散情况,而评分等频方式的数据是无法得到这样分析效果的。
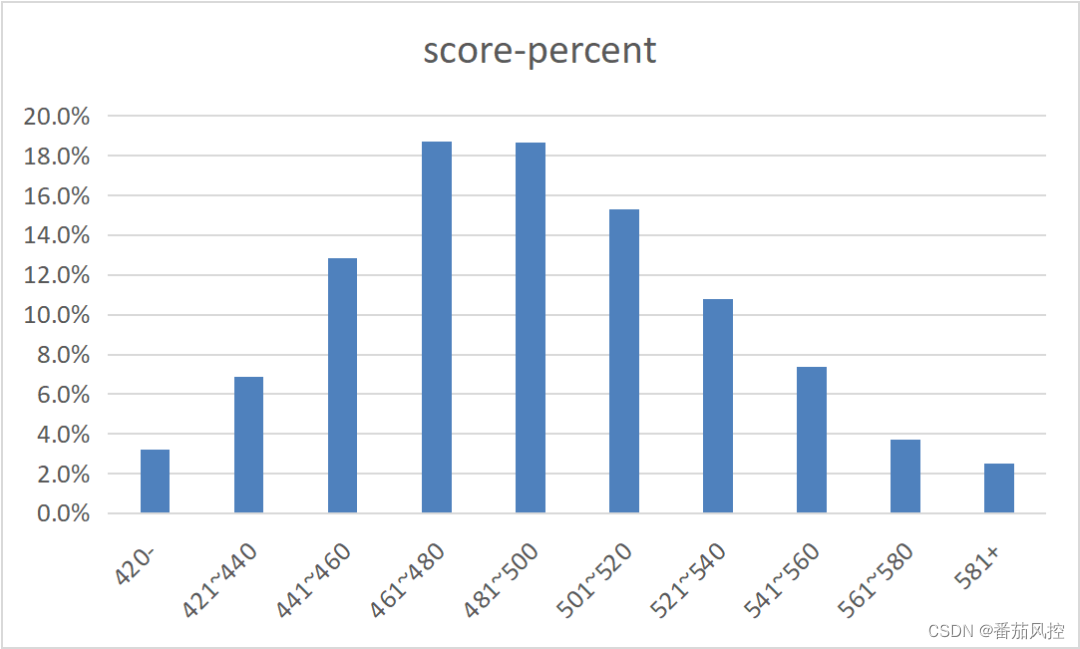
图8 评分等距的样本占比
因此,在我们分析样本模型评分的分布情况时,采用评分等距方式来展示数据更为合适,不仅可以有效描述模型评分与坏账响应的关系,而且能够合理探究模型评分与样本占比的形态。同时,这在确定模型决策阈值、客户风险评级、模型报告展示等方面也都是非常方便的。
以上内容便是信贷风控评分卡模型分数的转换逻辑介绍,大家需要重点理解模型概率到分数的映射关系,这是我们建模工作中必须熟悉掌握的。在实际业务场景中,针对分类模型问题,无论是采用逻辑回归传统算法,还是XGBoost、LightGBM等决策树算法,当模型结果输出概率之后,我们都可以结合业务特点与实际经验,通过设定评分卡的标准,然后将其转换为模型分数,从而便于制定相关的模型应用策略。此外,要根据不同场景下的评分卡模型,采用合适的模型实践方法,为信贷风控的精细化管理提供有效的保障,以实现风控模型的价值与意义。
本次关于模型内容,在星球资料分享中,我们还为大家准备一份关于模型监控报告的内容,详情如下:
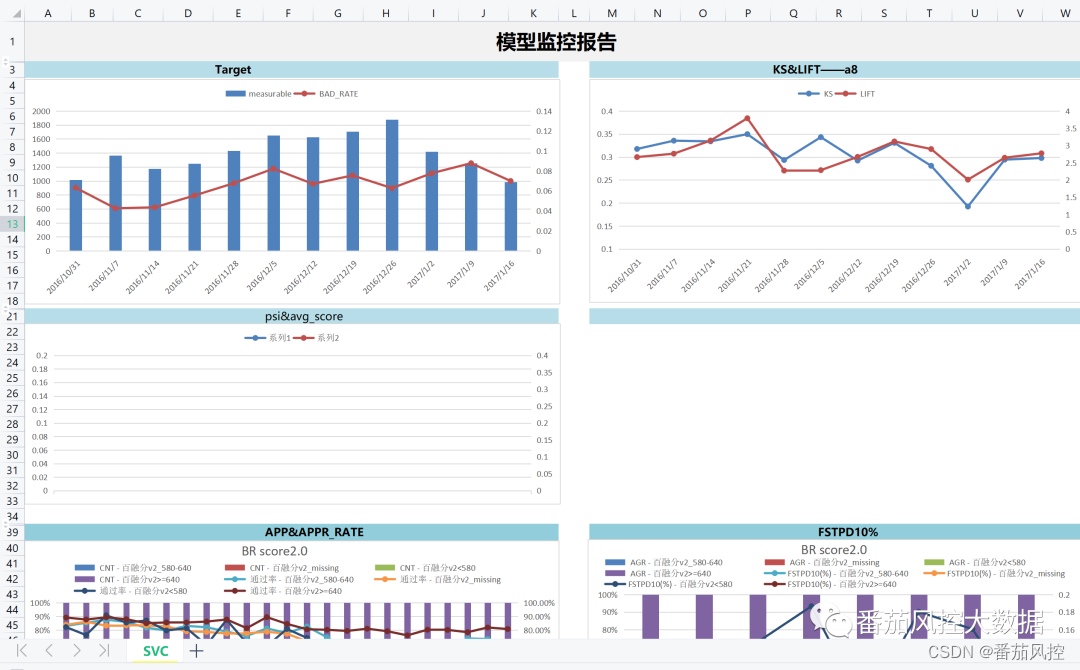
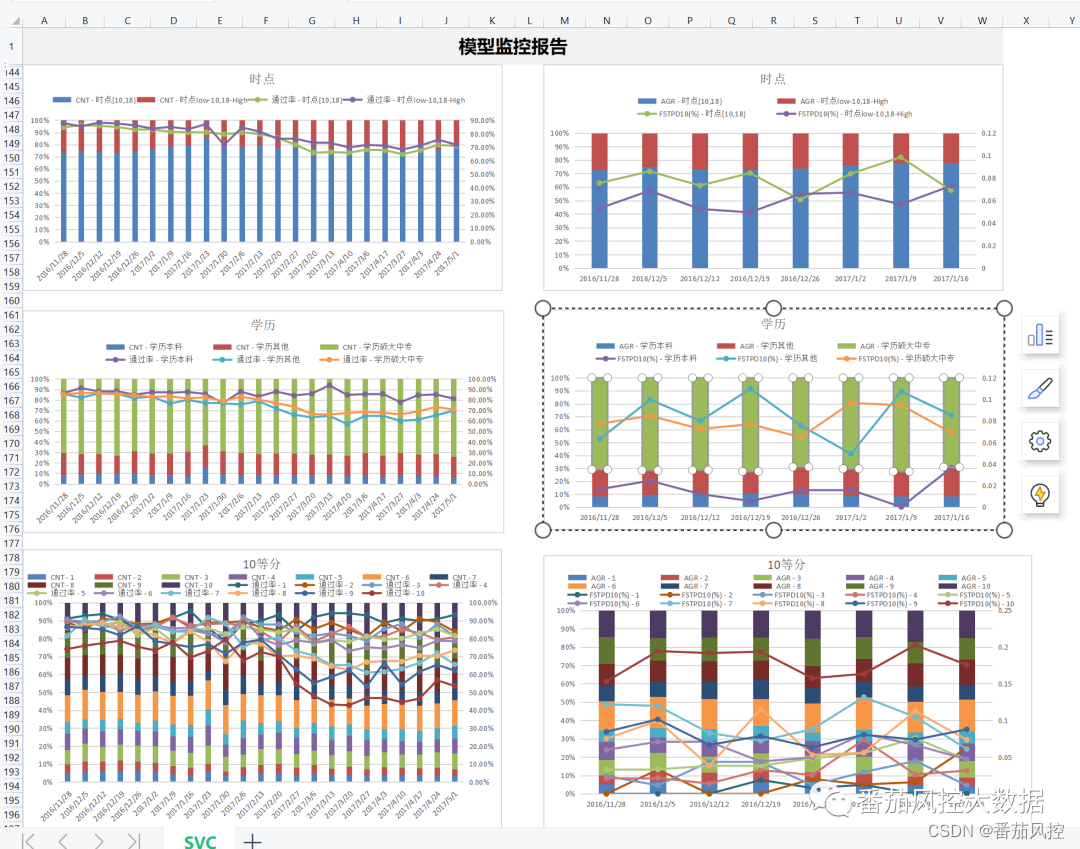
详情可移步知识星球查收此份内容:
…
~原创文章
边栏推荐
- Glide Mastery
- 《通信软件开发与应用》课程结业报告
- Glide advanced level
- Ad20 make logo
- [dark horse morning post] Luo Yonghao responded to ridicule Oriental selection; Dong Qing's husband Mi Chunlei was executed for more than 700million; Geely officially acquired Meizu; Huawei releases M
- Timed disappearance pop-up
- TypeError: Cannot read properties of undefined (reading ‘cancelToken‘)
- Excerpt from "sword comes" (VII)
- uniapp + uniCloud+unipay 实现微信小程序支付功能
- Constrained layout flow
猜你喜欢

【Vite】1371- 手把手开发 Vite 插件
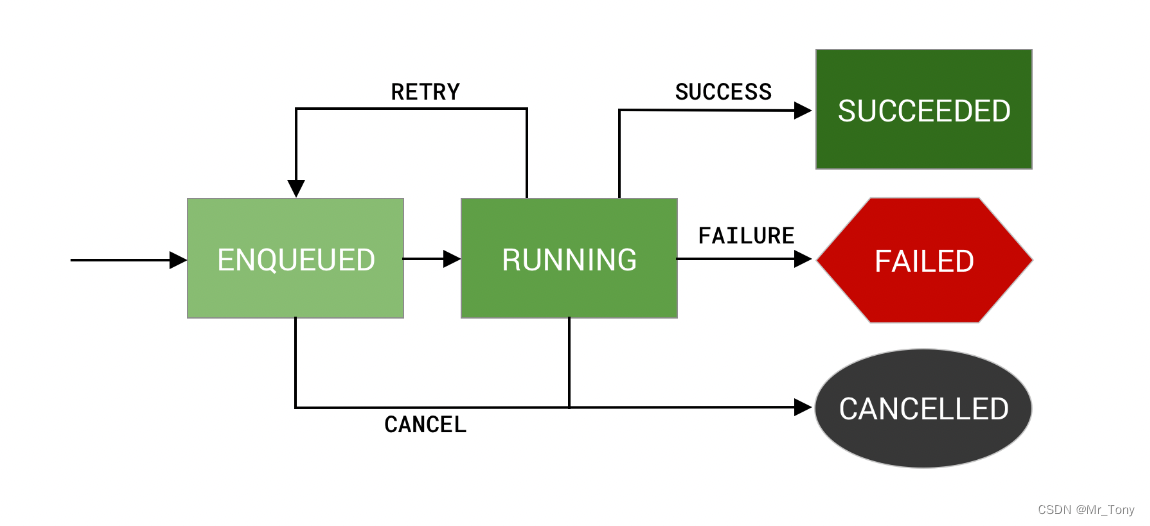
Learning II of workmanager

A large number of virtual anchors in station B were collectively forced to refund: revenue evaporated, but they still owe station B; Jobs was posthumously awarded the U.S. presidential medal of freedo
AD20 制作 Logo

ConstraintLayout的流式布局Flow
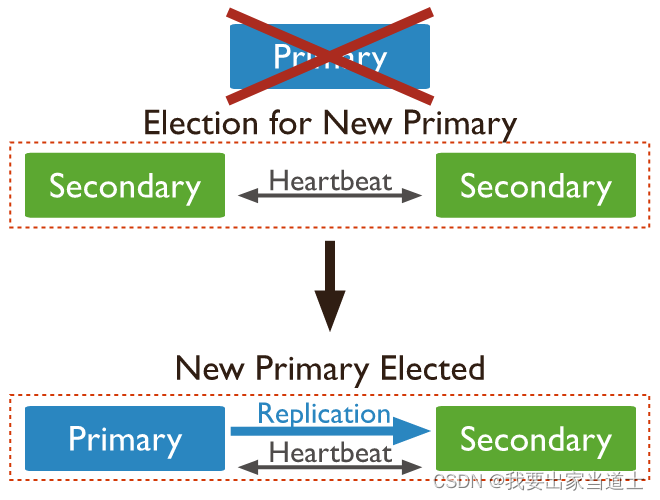
mongoDB副本集

Timed disappearance pop-up
Blockbuster: the domestic IDE is released, developed by Alibaba, and is completely open source!
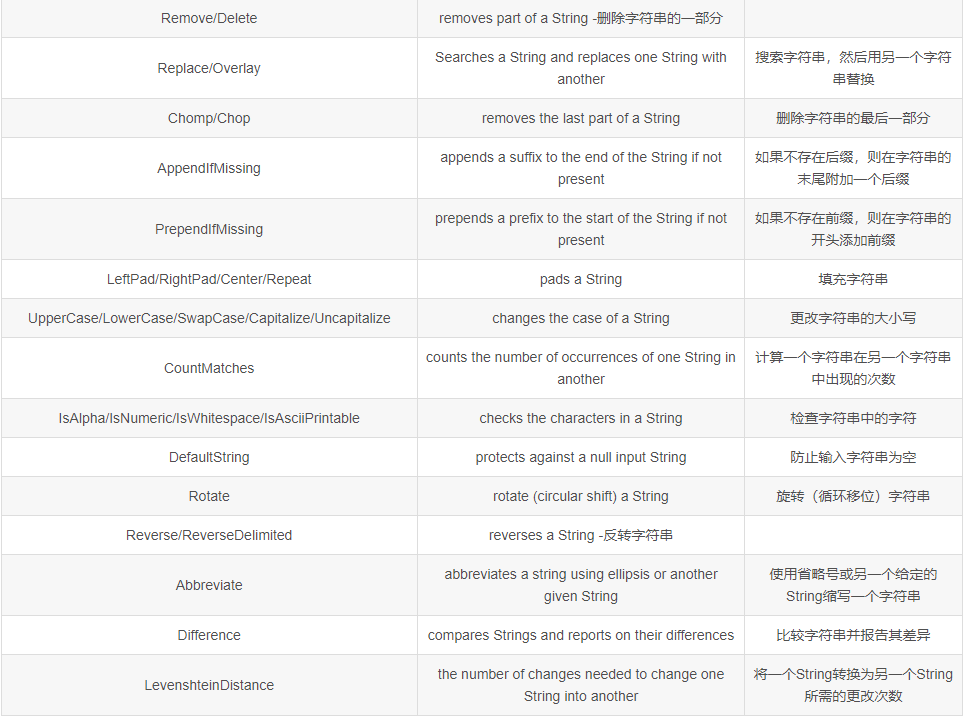
Usage differences between isempty and isblank
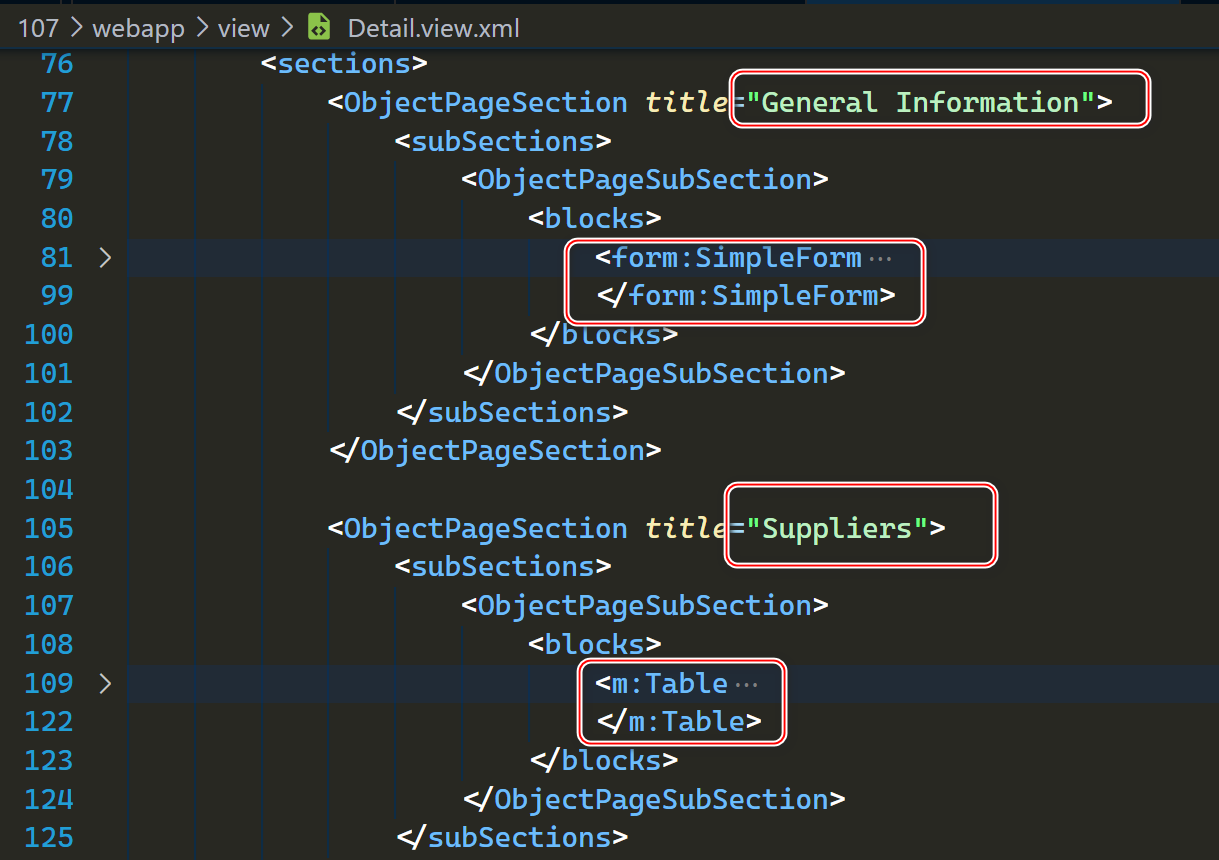
SAP UI5 ObjectPageLayout 控件使用方法分享
随机推荐
Idea create a new sprintboot project
How can non-technical departments participate in Devops?
A large number of virtual anchors in station B were collectively forced to refund: revenue evaporated, but they still owe station B; Jobs was posthumously awarded the U.S. presidential medal of freedo
> Could not create task ‘:app:MyTest.main()‘. > SourceSet with name ‘main‘ not found.问题修复
flex4 和 flex3 combox 下拉框长度的解决办法
Comparative learning in the period of "arms race"
Have the bosses ever encountered such problems in the implementation of flinksql by Flink CDC mongdb?
The horizontally scrolling recycleview displays five and a half on one screen, lower than the average distribution of five
php解决redis的缓存雪崩,缓存穿透,缓存击穿的问题
Who is the "conscience" domestic brand?
Swift set pickerview to white on black background
vscode的快捷键
字节跳动面试官:一张图片占据的内存大小是如何计算
Dedecms website building tutorial
非技術部門,如何參與 DevOps?
IDEA新建sprintboot项目
How does redis implement multiple zones?
pytorch输出tensor张量时有省略号的解决方案(将tensor完整输出)
TypeError: Cannot read properties of undefined (reading ‘cancelToken‘)
非技术部门,如何参与 DevOps?