当前位置:网站首页>[combinatorics] permutation and combination (examples of combinatorial number of multiple sets | three counting models | selection problem | combinatorial problem of multiple sets | nonnegative intege
[combinatorics] permutation and combination (examples of combinatorial number of multiple sets | three counting models | selection problem | combinatorial problem of multiple sets | nonnegative intege
2022-07-03 13:54:00 【Programmer community】
Arrange and combine reference blogs :
- 【 Combinatorial mathematics 】 Basic counting principle ( The principle of addition | Multiplication principle )
- 【 Combinatorial mathematics 】 Examples of permutation and combination of sets ( array | Combine | Circular arrangement | binomial theorem )
- 【 Combinatorial mathematics 】 Permutation and combination ( Arrange and combine content summary | Select the question | Set arrangement | Set combination )
- 【 Combinatorial mathematics 】 Permutation and combination ( Examples of permutations )
- 【 Combinatorial mathematics 】 Permutation and combination ( Multiset arrangement | Full Permutation of multiple sets | Multiset incomplete permutation The repetition of all elements is greater than the number of permutations | Multiset incomplete permutation The repetition of some elements is less than the number of permutations )
- 【 Combinatorial mathematics 】 Permutation and combination ( The combinatorial number of multiple sets | The repetition of all elements is greater than the number of combinations | The combinatorial number of multiple sets deduction 1 Division line derivation | The combinatorial number of multiple sets deduction 2 Derivation of the number of nonnegative integer solutions of indefinite equations )
One 、 Examples of multiset combinations
take
r
r
r It's the same ball , Put it in
k
k
k In different boxes , There is no limit to the number of balls in each box , Find the total number of ways to put the ball ?
There is no difference between balls , Put the ball in the box , The ball has no label , The box has a label , The number of balls in each box is different ;
The number of balls falling into each box is different , It's a different solution ;
hypothesis
n
n
n Boxes , The number of balls in each box is
x
1
,
x
2
,
⋯
,
x
k
x_1 , x_2 , \cdots , x_k
x1,x2,⋯,xk ;
There are indefinite equations :
x
1
+
x
2
+
⋯
+
x
k
=
r
x_1 + x_2 + \cdots + x_k = r
x1+x2+⋯+xk=r
Value :
x
1
,
x
2
,
⋯
,
x
k
x_1 , x_2 , \cdots , x_k
x1,x2,⋯,xk The value of is a nonnegative integer , It can take
0
∼
r
0 \sim r
0∼r Between the value of the ;
This problem can be equivalent to multiple sets
S
=
{
n
1
⋅
a
1
,
n
2
⋅
a
2
,
⋯
,
n
k
⋅
a
k
}
,
0
≤
r
≤
n
i
≤
+
∞
S = \{ n_1 \cdot a_1 , n_2 \cdot a_2 , \cdots , n_k \cdot a_k \} , \ \ \ 0 \leq r \leq n_i \leq +\infty
S={ n1⋅a1,n2⋅a2,⋯,nk⋅ak}, 0≤r≤ni≤+∞ Of
r
r
r Combinatorial number ;
N
=
C
(
k
+
r
−
1
,
r
)
N= C(k + r - 1, r)
N=C(k+r−1,r)
Reference resources : 【 Combinatorial mathematics 】 Permutation and combination ( The combinatorial number of multiple sets | The repetition of all elements is greater than the number of combinations | The combinatorial number of multiple sets deduction 1 Division line derivation | The combinatorial number of multiple sets deduction 2 Derivation of the number of nonnegative integer solutions of indefinite equations )
Above
r
r
r It's the same ball , Put it in
k
k
k In different boxes , The number of ways to put the ball is
N
=
C
(
k
+
r
−
1
,
r
)
N = C(k + r - 1, r)
N=C(k+r−1,r)
Two 、 Three counting models
Three counting models :
- ① Select the question :
- ② Multiple set combinatorial problem :
- ③ Nonnegative integer solution of the equation :
1. Select the question :
n
n
n Meta set
S
S
S , from
S
S
S Select... From the set
r
r
r Elements ;
according to Whether the element can be repeated , Whether the selection process is orderly , The selection question is divided into four sub types :
| Elements do not repeat | Elements can be repeated | |
|---|---|---|
| Orderly selection | Set arrangement P ( n , r ) P(n,r) P(n,r) | Multiset arrangement |
| Unordered selection | Set combination C ( n , r ) C(n,r) C(n,r) | Combination of multiple sets |
Select the question :
- Non repeatable elements , Orderly selection , Corresponding Arrangement of sets
- Non repeatable elements , Unordered selection , Corresponding A combination of sets
- Repeatable elements , Orderly selection , Corresponding Arrangement of multiple sets
- Repeatable elements , Unordered selection , Corresponding Combination of multiple sets
2. Multiple set combinatorial problem :
S
=
{
n
1
⋅
a
1
,
n
2
⋅
a
2
,
⋯
,
n
k
⋅
a
k
}
,
0
≤
n
i
≤
+
∞
S = \{ n_1 \cdot a_1 , n_2 \cdot a_2 , \cdots , n_k \cdot a_k \} , \ \ \ 0 \leq n_i \leq +\infty
S={ n1⋅a1,n2⋅a2,⋯,nk⋅ak}, 0≤ni≤+∞
- Type of elements : Multiple sets contain
k
k
k Different elements ,
- The element represents : Each element is represented as
a
1
,
a
2
,
⋯
,
a
k
a_1 , a_2 , \cdots , a_k
a1,a2,⋯,ak ,
- Element number : The number of occurrences of each element is
n
1
,
n
2
,
⋯
,
n
k
n_1, n_2, \cdots , n_k
n1,n2,⋯,nk ,
- The value of the number of elements :
n
i
n_i
ni The value requirement of is Greater than
0
0
0 , Less than positive infinity
+
∞
+ \infty
+∞ ;
Combination of the above multiple sets , When The repeatability of all elements
n
i
n_i
ni The number of groups is greater than the number of combinations
r
r
r when ,
r
≤
n
i
r \leq n_i
r≤ni when , The combination number of multiple sets is
N
=
C
(
k
+
r
−
1
,
r
)
N= C(k + r - 1, r)
N=C(k+r−1,r)
3. Nonnegative integer solutions of indefinite equations :
x
1
+
x
2
+
⋯
+
x
k
=
r
x_1 + x_2 + \cdots + x_k = r
x1+x2+⋯+xk=r
The number of nonnegative integer solutions is :
N
=
C
(
k
+
r
−
1
,
r
)
N= C(k + r - 1, r)
N=C(k+r−1,r)
边栏推荐
- Depth and breadth first traversal of tree (regardless of binary tree)
- Leetcode-1175. Prime Arrangements
- Use vscode to view hex or UTF-8 codes
- logback日志的整理
- SQL Injection (GET/Search)
- Complete deep neural network CNN training with tensorflow to complete picture recognition case 2
- Unable to stop it, domestic chips have made another breakthrough, and some links have reached 4nm
- 常见的几种最优化方法Matlab原理和深度分析
- 解决MySql 1045 Access denied for user ‘root‘@‘localhost‘ (using password: YES)
- 掌握Cypress命令行选项,是真正掌握Cypress的基础
猜你喜欢
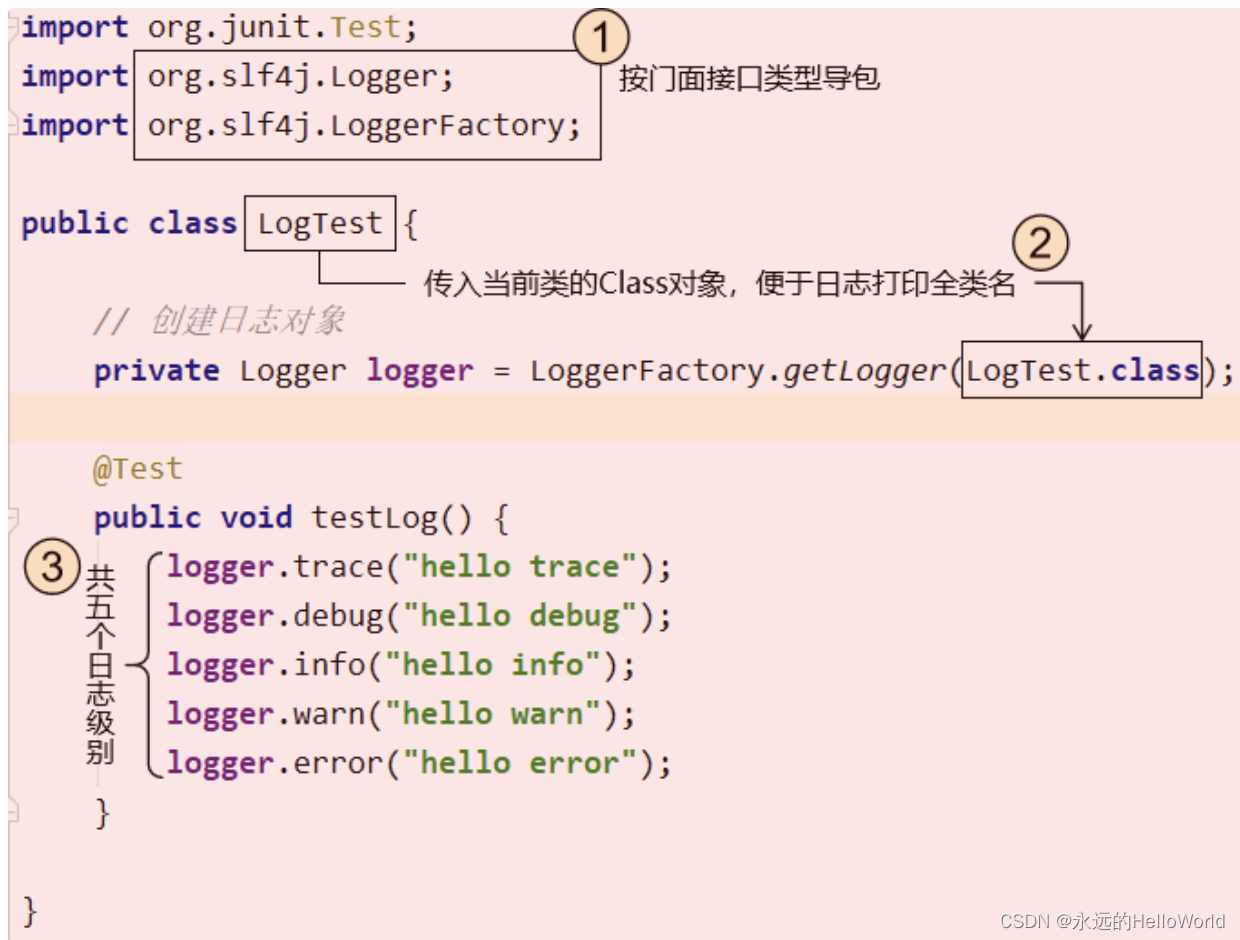
Logback log sorting

Can newly graduated European college students get an offer from a major Internet company in the United States?

logback日志的整理
GoLand 2021.1: rename the go project
KEIL5出现中文字体乱码的解决方法

SQL Injection (POST/Select)

使用vscode查看Hex或UTF-8编码

Complete deep neural network CNN training with tensorflow to complete picture recognition case 2
![[technology development-24]: characteristics of existing IOT communication technology](/img/f3/a219fe8e7438b8974d2226b4c3d4a4.png)
[technology development-24]: characteristics of existing IOT communication technology

Qt学习23 布局管理器(二)
随机推荐
Use and design of Muduo buffer class
Brief analysis of tensorboard visual processing cases
解决MySql 1045 Access denied for user ‘root‘@‘localhost‘ (using password: YES)
How to use lxml to judge whether the website announcement is updated
Static linked list (subscript of array instead of pointer)
GoLand 2021.2 configure go (go1.17.6)
php 迷宫游戏
[bw16 application] instructions for firmware burning of Anxin Ke bw16 module and development board update
使用Tensorflow进行完整的深度神经网络CNN训练完成图片识别案例2
TensorBoard可视化处理案例简析
8 Queen question
Flutter dynamic | fair 2.5.0 new version features
[développement technologique - 24]: caractéristiques des technologies de communication Internet des objets existantes
User and group command exercises
[技术发展-24]:现有物联网通信技术特点
全面发展数字经济主航道 和数集团积极推动UTONMOS数藏市场
[机缘参悟-37]:人感官系统的结构决定了人类是以自我为中心
软件测试工作那么难找,只有外包offer,我该去么?
实现CNN图像的识别和训练通过tensorflow框架对cifar10数据集等方法的处理
Go: send the get request and parse the return JSON (go1.16.4)