2-3 lookup tree

2-3 Search tree (2-3-Search-Tree)

• 2- node ： The nodes in a standard binary tree are called 2- node （ It has a key and two links ）.
• 3- node ： Contains two keys and three links .

Definition ： One 2-3 Find a tree or an empty tree , Or composed of the following nodes :

2- node , It has a key （ And its corresponding value ） And two links , The left link points to 2-3 All the keys in the tree are smaller than this node , The right link points to 2-3 All the keys in the tree are larger than this node .

3- node , It has two keys （ And its corresponding value ） And three links , The left link points to 2-3 All the keys in the tree are smaller than this node , Link to 2-3 The keys in the tree are located in the Between two keys , The right link points to 2-3 All the keys in the tree are larger than this node .

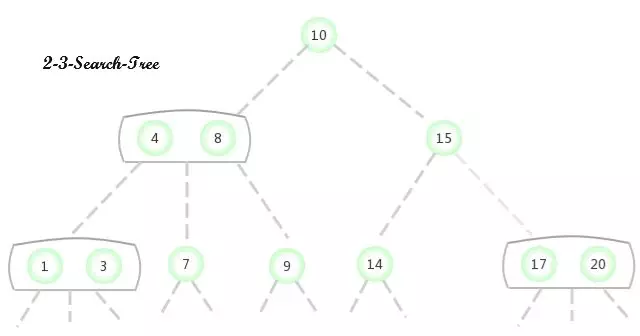
2-3 Search tree (2-3-Search-Tree) operation

A perfectly balanced 2-3 The distance between all empty links in the search tree and the root node should be the same .

lookup

2-3 The search in the search tree is similar to the search in the binary search tree . To determine whether a key is in the tree , First compare it with the key in the root node . If it and any one of them equal , Find hits . otherwise , Find the link to the corresponding interval according to the comparison results , And recursively continue to search in the subtree it points to . If it is an empty link , Find misses .

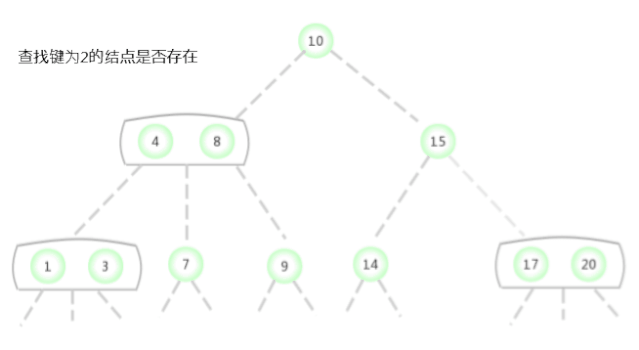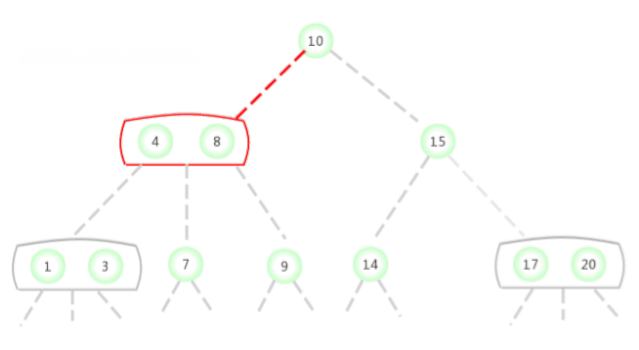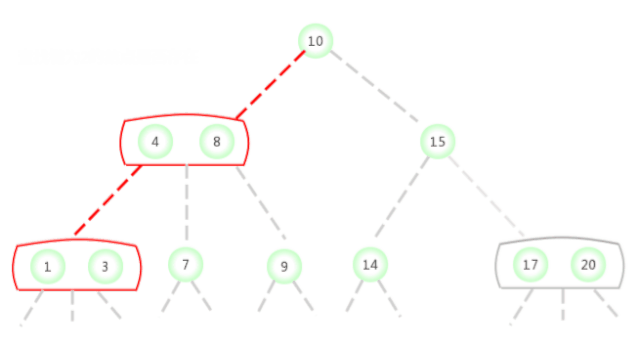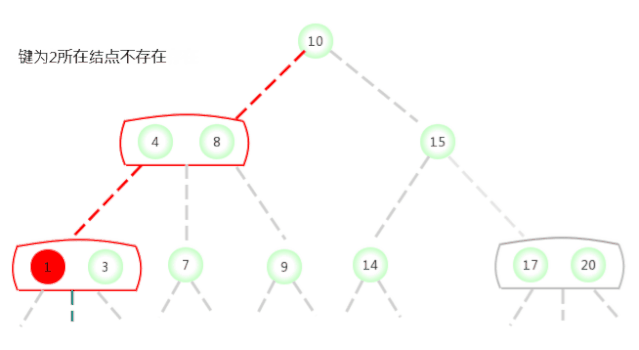
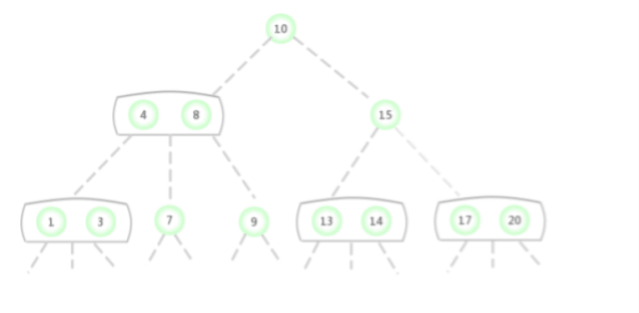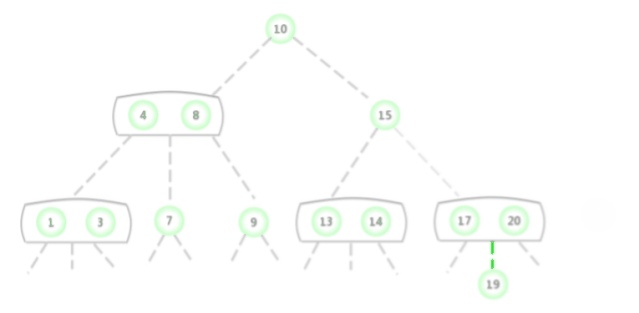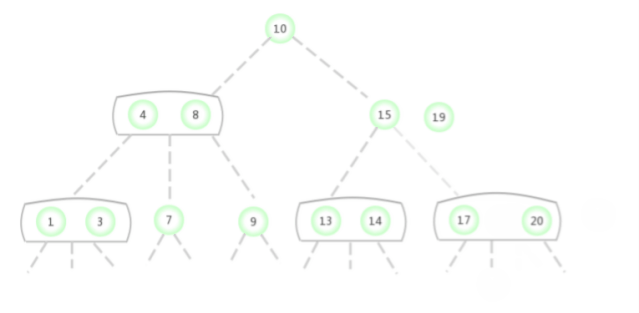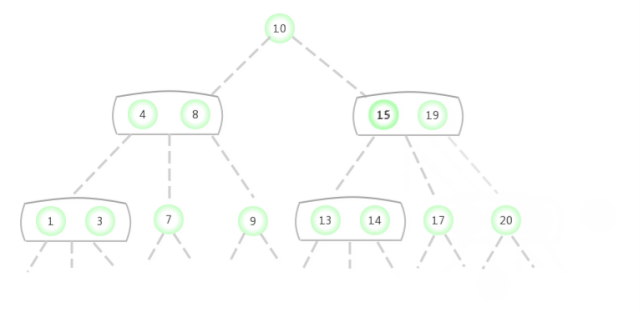
In the picture above 2-3 The search key in the tree is 2 Whether the node exists , The process is as follows ：

In the picture above 2-3 The search key in the tree is 17 Whether the node exists , The process is as follows ：

Insert

towards 2- Insert a new key in the node

To be in 2-3 Insert a new node into the tree , Similar to the insertion of binary search tree , First perform a miss search , Find the location of the node to be inserted , Hang it at the bottom of the tree . But in this way, the tree cannot guarantee perfect balance . Use 2-3 The main reason is ： After inserting new nodes, you can continue to maintain balance .

If the missed lookup ends with a 2- node , Will this 2- node Replace with 3- node , Save the key to be inserted in it .

If the missed lookup ends with a 3- node , The analysis process is as follows .

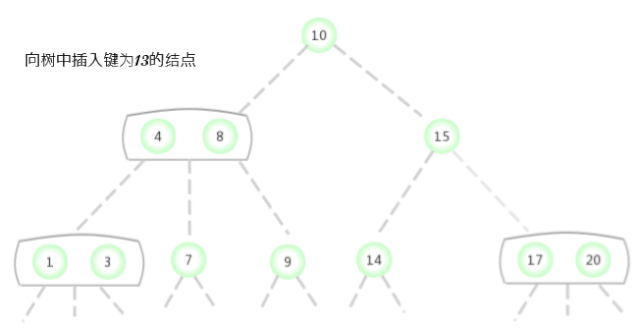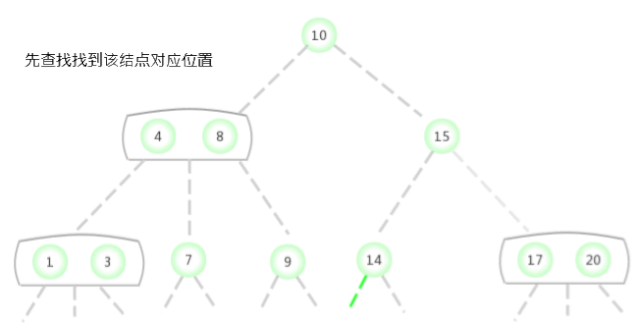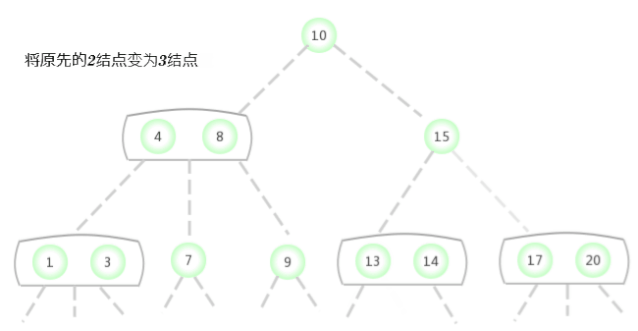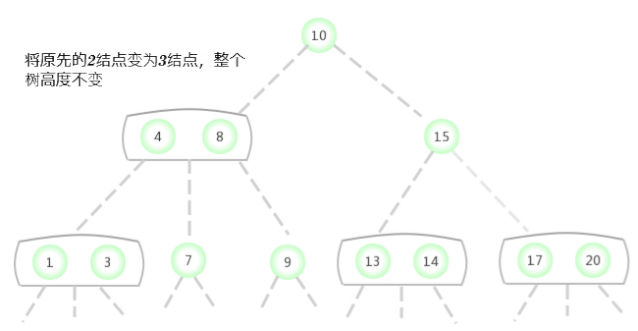
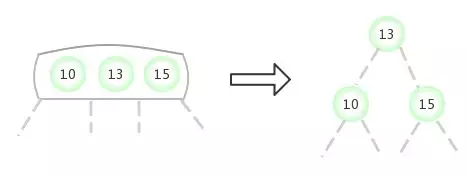
To a tree that contains only one 3- Insert a new key into the tree of the node

Before considering the general situation , Let's assume that we need a tree that contains only one 3- Insert a new key into the tree of the node . There are two keys in this tree , So in its only node There is no room to insert new keys . To insert a new key , First, temporarily store the new key in this node , To form a 4- node ( contain 3 Keys and 4 link ). Create a 4- node Very convenient , Because it is easy to transform it into a tree made of 3 individual 2- node Composed of 2-3 Trees , One of the nodes ( root ) Contains the middle key , A node contains 3 The smallest of the keys ( Connected to the left link of the root node ), A node contains 3 The largest of the keys ( Connect with the right link of the root node ). This tree is a tree that contains 3 Binary search tree of nodes , It is also a perfectly balanced tree 2-3 Trees , Because all of them The distance between empty links and nodes is equal . The height of the tree before insertion is 0, The height of the inserted tree is 1.

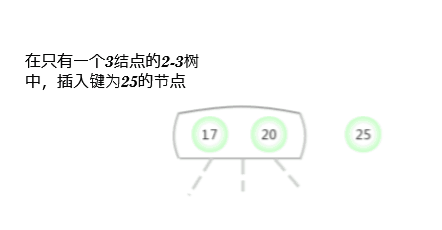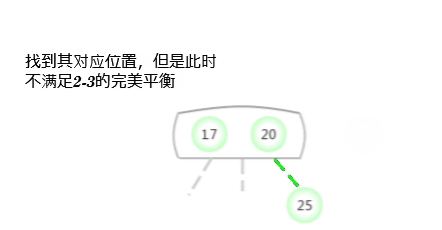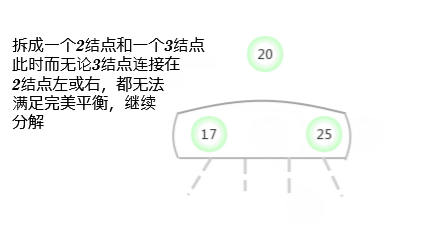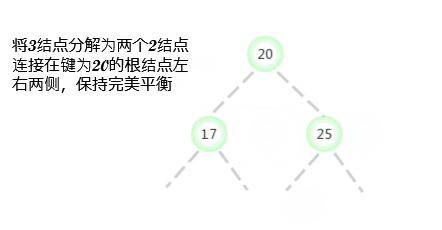
To a parent node is 2- Nodal 3- Insert a new key in the node

Suppose that a miss lookup ends in a 3- node , And its parent node is a 2- node . In this case, it's necessary ： Under the premise of maintaining the perfect balance of the tree, it is the new key Make room . You need to construct a temporary 4- node And decompose it , But at this time, a new node will not be created for the middle key , Instead, move it to the original parent node .

Regard this transformation as pointing to the original 3- node Replace one link of the new parent node with two links on the left and right sides of the original middle key , And point to two new 2- node . Based on assumptions , Of the oil space in the parent node ： The parent node is a 2- node , After inserting, it becomes a 3- node . in addition , This conversion does not affect ( Perfectly balanced )2-3 Trees Of The main properties . The trees are still in order , Because the middle key is moved to the parent node ; The tree is still perfectly balanced , After insertion, the distance from all leaf nodes to the root node is still the same .

The above process is 2-3 The core of tree dynamic change , The diagram shows as follows ：

To a parent node is 3- Nodal 3- Insert a new key in the node

Assume that the Miss lookup ends with a parent node of 3- node Of 3- node . Still need to construct a temporary 4- node And decompose it , Then insert its middle key into its parent node . Because the parent node is also a 3- node , After inserting into the middle, a new temporary 4- node , Then do the same transformation on this node , Set decomposes this parent node and inserts its middle key into its parent node . Generalize to the general situation , That's how we keep breaking up the temporary 4- node And insert the middle key into the parent node at a higher level , Until I met a 2- node And replace it with one that does not need further decomposition 3- node , Or to arrive 3- node The root of the .

The process is as follows ：

Decompose the root node

If the path from the inserted node to the root node is 3- node , The root node eventually becomes a temporary 4- node . At this time, there is only one tree *3- node The method of inserting new keys into the tree of . Will be temporary 4- node Break it down into three 2- node **, Tree height plus 1. This last change still maintains the perfect balance of the tree , Because it transforms the root node .

The process is as follows ：

4- Decomposition of nodes

stay 2-3 Trees in 4- node There are the following situations in the location .

• 1. Root node
• 2. The parent node is 2- node Left child node or right child node of
• 3. Parent node is 3- node The left child of 、 Middle child node or right child node

Now let's take a detailed look at 2-3 Trees How to decompose when the above positions appear in .

situation ：

Be temporary 4- node Appears at the root node ：

Be temporary 4- node Appear in the 2- node The left side of the ：

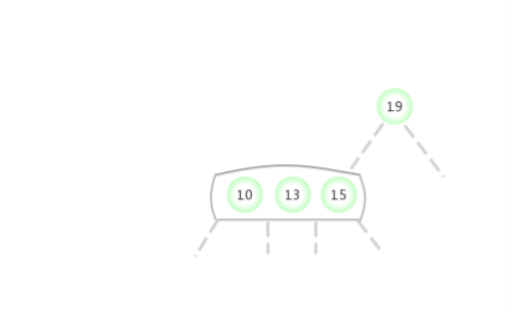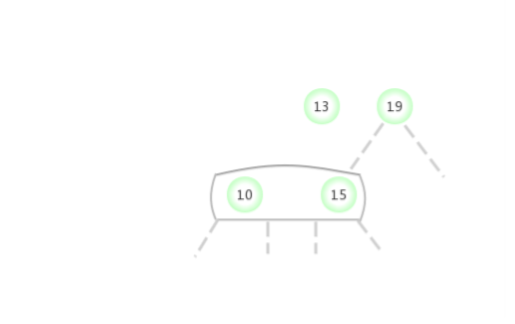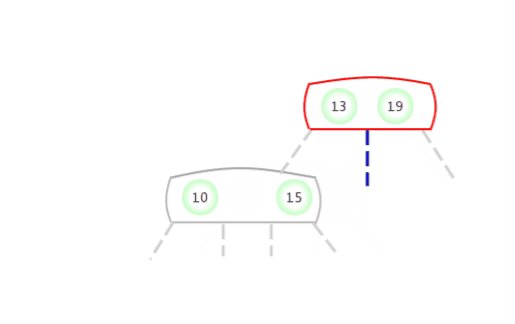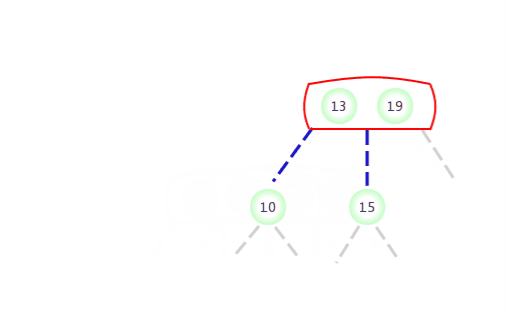
Be temporary 4- node Appear in the 2- node The right side of the ：

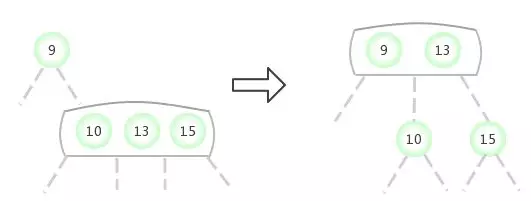
Be temporary 4- node Appear in the 3- node The left side of the ：

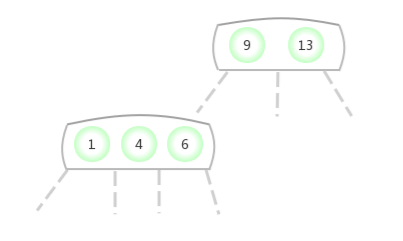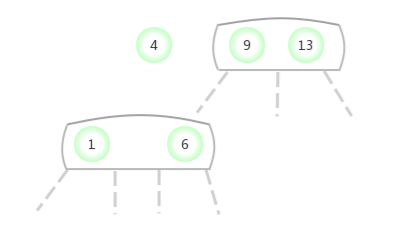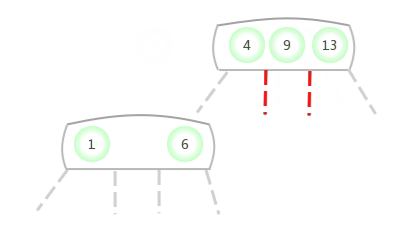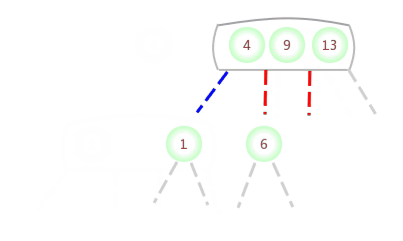
Be temporary 4- node Appear in the 3- node In the middle of the ：

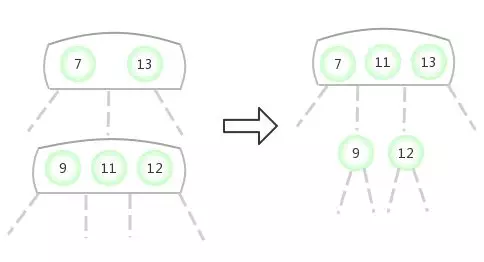
Be temporary 4- node Appear in the 3- node The right side of the ：

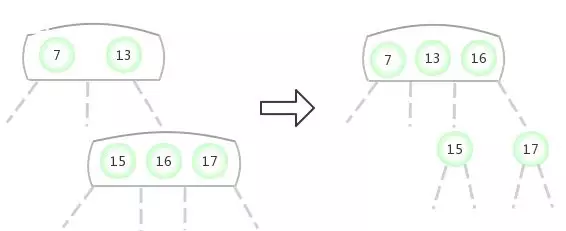
In the above case , In the process of change , Only when the root node is finally temporary 4- node , At this time, it is decomposed into 3 individual 2- node when , The height of the whole tree will increase 1. besides , Insert a node 2-3 The height of the tree is still the original height . In the above change process ： The path length of any empty link to the root node is equal .

Conclusion

In a tree the size is N Of 2-3 In the tree , The nodes accessed by the search and insert operations will not exceed lgN.

• prove ： A tree contains N Of nodes 2-3 The height of the tree is log2 N and log3 N Between .