当前位置:网站首页>ICML 2022 | Meta propose une méthode robuste d'optimisation bayésienne Multi - objectifs pour faire face efficacement au bruit d'entrée
ICML 2022 | Meta propose une méthode robuste d'optimisation bayésienne Multi - objectifs pour faire face efficacement au bruit d'entrée
2022-07-05 17:25:00 【Paperweekly】

Auteur | Yang zequn
Unité | Renmin University of China
Orientation de la recherche | Apprentissage multimodal

Titre de l'article:
Robust Multi-Objective Bayesian Optimization Under Input Noise
Liens vers les articles:
https://arxiv.org/abs/2202.07549
Liens vers les projets:
https://github.com/facebookresearch/robust_mobo
Cet article est facebook Publié dans ICML 2022 Un travail,Il analyse théoriquement l'optimisation bayésienne Multi - objectifs avec le bruit d'entrée.

Introduction
Dans cet article, le problème du bruit d'entrée pour l'optimisation Multi - objectifs , Combiné à l'optimisation bayésienne et à l'optimisation Pareto, la valeur à risque Multi - objectifs globale est conçue et optimisée. , Pour résoudre le problème des contraintes de boîte noire sensibles au bruit d'entrée . Optimisation bayésienne en ajustant les paramètres de conception , Les indicateurs de performance de la boîte noire peuvent être optimisés pour un coût d'évaluation élevé . Bien que de nombreuses méthodes existantes soient proposées pour optimiser un seul objectif sous le bruit d'entrée , Cependant, il n'existe toujours pas de méthode permettant de résoudre le problème réel de la sensibilité des cibles multiples aux perturbations d'entrée. .
Dans ce travail, L'auteur propose la première méthode bayésienne robuste Multi - objectifs pour faire face au bruit d'entrée . L'auteur formalise l'objectif en optimisant la mesure du risque d'un objectif incertain , C'est - à - dire la valeur de risque Multivariable (MVaR). Grâce à l'optimisation directe MVaR Dans de nombreux cas, il n'est pas possible de calculer , Les auteurs proposent un 、 Une approche théorique utilisant des échelles aléatoires pour optimiser MVaR. Expérimentalement , Cette méthode est nettement supérieure à d'autres méthodes dans l'ensemble de données , Et réalise efficacement la conception la plus robuste .
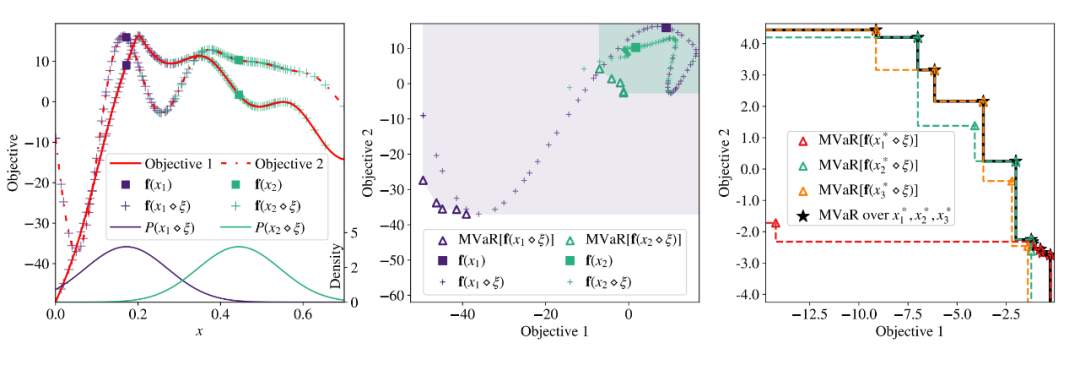
▲ Fig.1: L'optimisation Multi - objectifs de la conception non robuste est sensible au bruit d'entrée sur un ensemble de données simple , La démonstration de la sélection de l'ensemble le plus avantageux est donnée. .
Voici le diagramme 1 Pour clarifier les questions soulevées par l'auteur :Sur la photo de gauche, Conception non robuste (Violet ) Et un design robuste (Vert ) La valeur nominale de est représentée par un carré . Le signe plus indique la valeur cible de chaque conception avec un bruit d'entrée gaussien moyen nul ,L'écart type est 0.1.Je vois., Bien qu'une conception non robuste puisse donner des résultats localement meilleurs , Mais son instabilité sous perturbation d'entrée , Facile à conduire à de pires performances ; Et un design robuste Le résultat est moins perturbateur pour l'entrée , Insensible au bruit d'entrée .
Le graphique du milieu est conçu pour être non robuste et robuste MVaR Description de l'ensemble , Où le triangle représente la distribution du bruit d'entrée , Chaque Design MVaR Approximation discrète de l'ensemble . Sans tenir compte du bruit ,Violet Les carrés correspondent à de meilleures valeurs ; Mais il y a un risque de perturbation (MVaR)Plus grande, Il est difficile d'être robuste au bruit d'entrée . Ainsi, la stabilité de la solution peut être caractérisée par des valeurs de risque multivariables . La figure de droite est une description des stratégies de sélection des différents ensembles de risques , La méthode de l'hypothèse donne trois objectifs MVaR Ensemble, L'ensemble optimal de risques est un objectif différent MVaR L'ensemble le plus avantageux sur l'Union de l'ensemble .

Contexte
Optimisation Multi - objectifs pour équilibrer plusieurs fonctions de boîte noire , L'objectif est d'identifier la limite Pareto du compromis optimal et l'ensemble Pareto correspondant de la conception optimale. . Envisager de maximiser la fonction de la boîte noire : Parmi eux , Est le nombre de cibles, C'est un espace de recherche serré . Et la définition ci - dessus peut conduire à la définition de la domination Pareto et de la limite Pareto .Si vecteur Pareto domine ,Note ,Si et seulement si Et Satisfaction .
Pareto Optimum (Pareto optimality) Est un état qui ne peut plus être amélioré , Il est impossible d'améliorer certains critères d'individu ou de préférence sans compromettre d'autres. . Si un état a une amélioration Pareto optimale , On l'appelle Pareto. . Un état qui n'est pas dominé par Pareto , On l'appelle Pareto Optimum ou Pareto efficace , Parmi les problèmes d'optimisation peut être considéré comme le plus grand avantage . L'ensemble de ces meilleures compositions s'appelle la limite Pareto .Comme le montre la figure ci - dessous,A Et B C'est le point sur la frontière Pareto , C'est pour C La domination de .
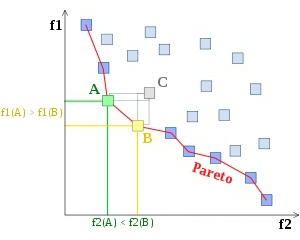
▲ Fig.2: Voici un exemple de limite Pareto . Les points de l'ensemble représentent des choix réalisables , Ici, les valeurs plus faibles sont considérées comme meilleures , La ligne rouge représente la frontière Pareto , Tous les points d'échantillonnage ci - dessus sont valides pour Pareto .Point C En même temps A Et point B Domination, Donc ce n'est pas à la limite de Pareto .Point A Et point B Ne pas être strictement contrôlé par d'autres points , Donc sur la frontière .
Défini ici La frontière Pareto :
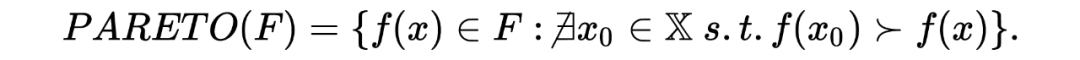
Si PARETO Les éléments satisfont aux contraintes supplémentaires de la boîte noire , L'ensemble de conception optimal correspondant est considéré comme la limite Pareto .Et puis, L'auteur définit les mesures ( Hypervolume et incréments hypervolume ) Pour mesurer la qualité des différentes frontières Pareto , C'est - à - dire la mesure de la zone contenue à l'intérieur de la limite Pareto .

Méthodes
Il faut d'abord définir le risque . Étant donné que les mesures de risque attendues peuvent ne pas toujours être conformes à l'objectif de robustesse réelle , Donc ici, l'analyse des risques probabilistes , Et obtenir la définition suivante :
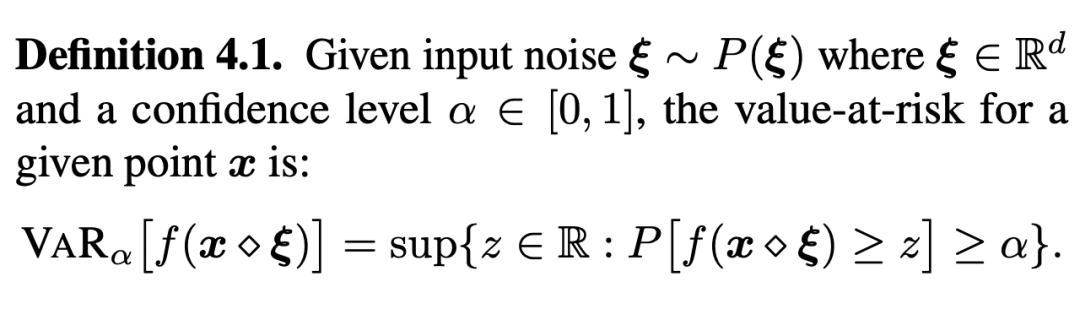
La définition de la var est donnée ci - dessus. , Il a été obtenu dans le bruit Une limite inférieure de ,De faire Au moins. La probabilité de tomber sur plus de Dans le domaine de , Et c'est ce qu'on appelle le risque probabiliste , Pour mesurer le bruit d'une seule cible .
Et pour Multivariate Value-at-Risk(MVaR)En termes,Tous les Les objectifs ont été évalués dans le même échantillon bruyant . L'auteur conçoit des limites Multi - objectifs qui sont des limites Pareto pour différentes cibles ,Peut être écrit sous la forme suivante:
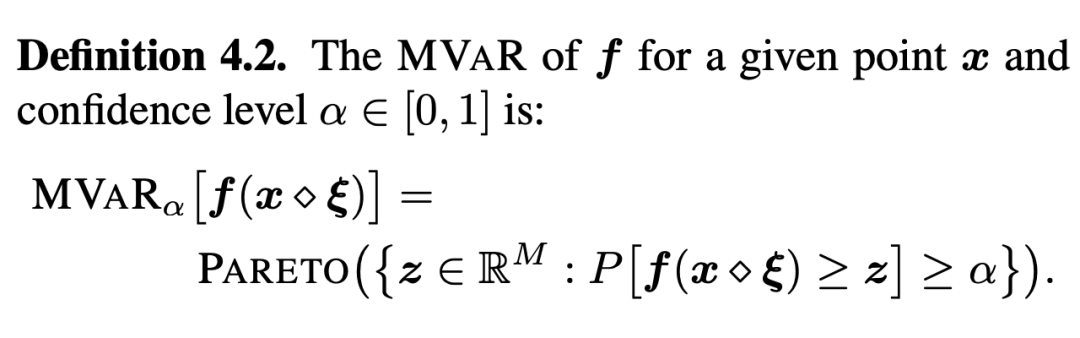
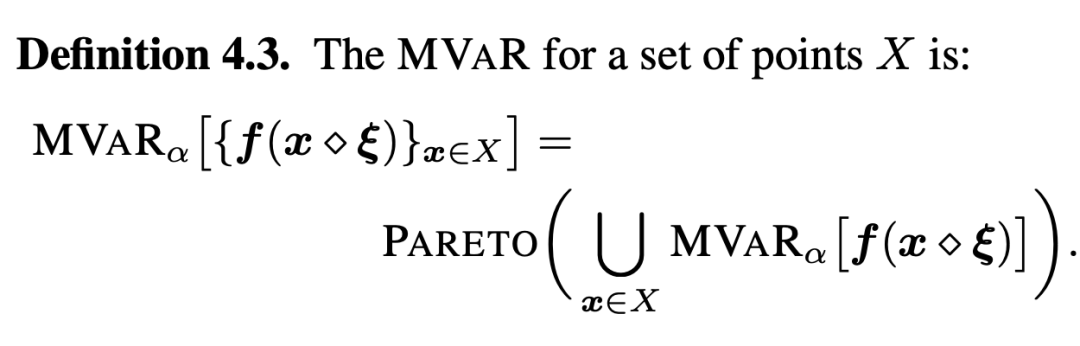
Par conséquent,, Il définit les risques globaux dans l'espace de conception , Est d'utiliser une série de points (Voir fig. 1 Triangle de), Approximation robuste de la limite de Pareto dans un environnement Multi - objectifs , C'est aussi l'une des contributions importantes de cet article .
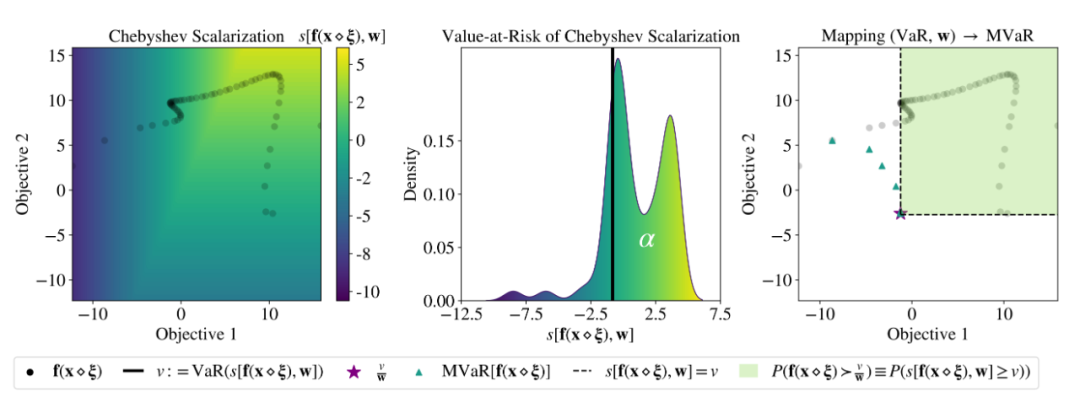
▲ Fig.3:Pour les graphiques1MoyennetoyLes donnéesMVaRLe processus de construction de
Cet article propose MARS Méthodes, En introduisant l'échelle de Chebyshev, VaR Et MVaR Relations,Et peut - être MVaR Ensemble pour l'estimation . Voici la photo. 3 C'est vrai 1 Données simples MVaR Processus de construction de collections , Où le point noir dans la figure de gauche indique que pour l'écart type est 0.1,La moyenne est 0 La valeur en fonction de la perturbation d'entrée gaussienne de , L'arrière - plan est un contour montrant les valeurs d'échelle de Chebyshev à travers l'espace cible . Le graphique du milieu montre la densité de probabilité de l'échelle de Chebyshev et Valeur de risque de l'échelle Chebyshev de , La masse de probabilité à droite de la ligne noire est égale à . La figure de droite montre la relation construite par le théorème prouvé dans cet article ,Oui. VaR Mapping to MVaR Moyenne, Le triangle vert représente la distribution du bruit d'entrée MVaR Approximation discrète de l'ensemble .

Principaux résultats
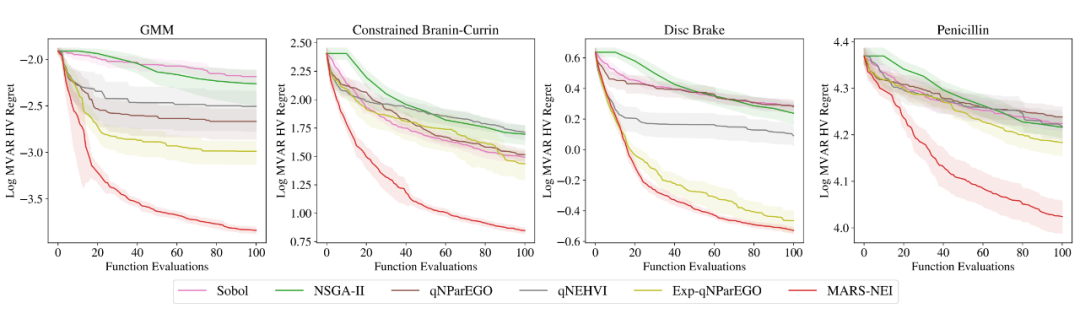
▲ Fig.4:In4 Évaluation sur différents ensembles de données sur le bruit
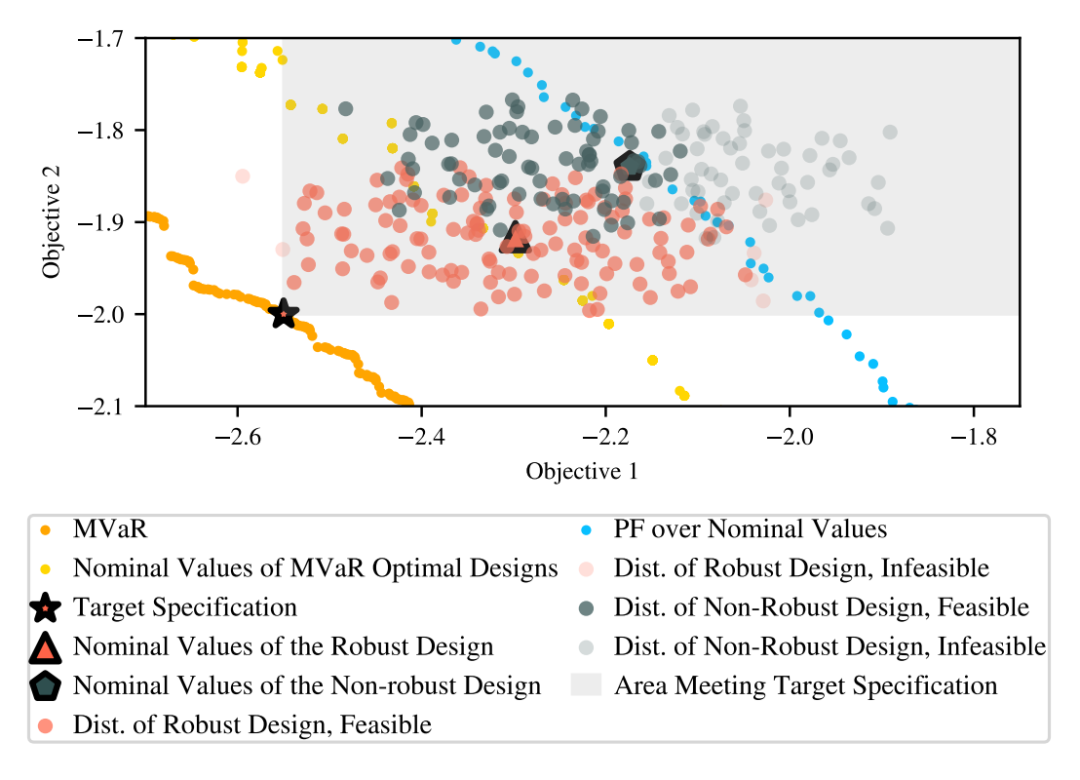
▲ Fig.5: Bien que la conception non robuste soit utilisée dans des cibles non bruyantes (Nominal Values) Ce qui suit est faisable , Mais il est situé près de la limite de la zone réalisable dans l'espace de conception , Les contraintes de la boîte noire peuvent être violées en cas de perturbation d'entrée , Rendre impossible la solution obtenue
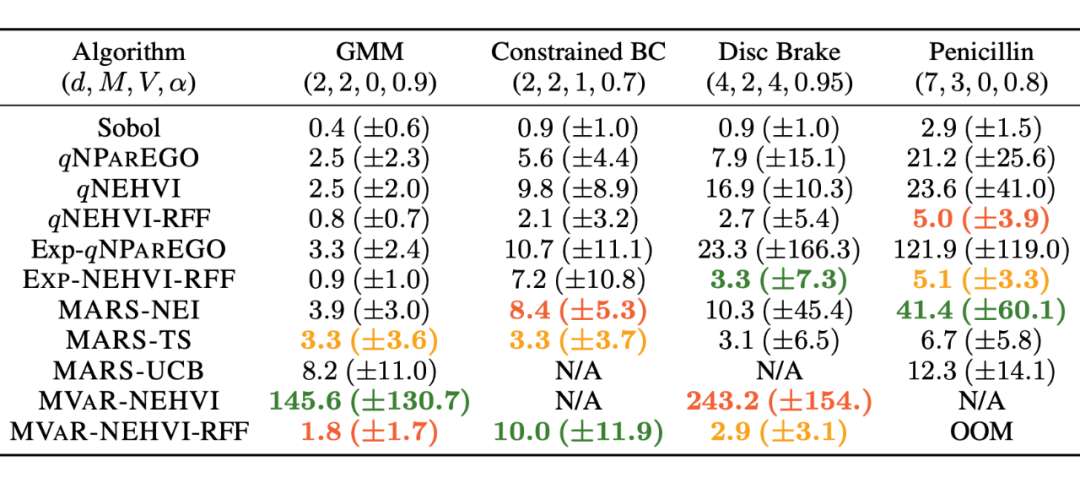
▲ Tableau1: Les bayésiens des différents algorithmes optimisent le temps d'exécution de chaque itération
Fig. 4 Montre les changements au fur et à mesure que la formation progresse , Performance de chaque algorithme , Ici, Global MVaR Et la conception MVaR De l'écart HV La valeur de la paire est utilisée comme indice d'évaluation , Peut expliquer la conception MVaR Est - ce que l'approche globale . Avec l'intervention du bruit d'entrée , Les méthodes non robustes sont significativement plus faibles que les méthodes robustes , Et la méthode de l'auteur est due à d'autres méthodes de comparaison .Fig. 5 Montre dans un véritable ensemble de données , Choisir les avantages d'un design robuste et d'un design non robuste . On peut voir ici à travers MVaR La conception apprise est plus proche de la valeur cible , Les solutions obtenues par des conceptions non robustes sont plus susceptibles de tomber dans des domaines non réalisables .Tableau 1 Et montre MARS-based Avantages de la méthode en termes de temps d'exécution .

Résumé et réflexion
Dans ce travail, L'auteur combine les propriétés de l'optimisation bayésienne et de la fusion Multi - objectifs , Le bruit d'entrée est analysé au niveau de la distribution , Il est conçu pour MVaR Risques et recherche de Pareto optimum pour les risques Multi - objectifs , Combine bien les caractéristiques des deux méthodes , L'idée est simple et raisonnable . Optimisation d'autres cibles multisources , Comme multimodal 、Perspectives multiples、 Pour l'apprentissage multitâche , Cette approche nous permet de commencer du point de vue du risque de perturbation des données , Pour analyser les problèmes potentiels de bruit d'entrée dans la méthode .
En même temps, Parce que la méthode est simple mais difficile à décrire visuellement , L'auteur a mis moins d'espace pour obtenir une explication claire de la méthode , Ensuite, le contexte et les principales contributions de l'article sont clairement exposés par un grand nombre de pavés. , Et un grand nombre de preuves sont données en annexe pour prouver la justesse du lemma .En même temps, L'auteur n'illustre les principaux problèmes et méthodes qu'à travers deux images , Montre clairement les problèmes de robustesse dans des situations Multi - objectifs .
Et au niveau méthodologique , La méthode utilise une série de points pour estimer les limites de distribution , Il est basé sur anchor Méthode, L'idée d'estimer la distribution des données par la sélection des ancrages est similaire , Les deux décrivent respectivement les limites de distribution et la distribution . Par la suite, le bruit ( Bruit d'entrée 、Bruit des étiquettes) Dans ce cas, une réflexion approfondie sur la relation entre les deux .
Lire la suite

#Allez. Projet OK. Dow.#
Que vos mots soient plus visibles
Comment faire en sorte que plus de contenu de haute qualité atteigne le public sur un chemin plus court,Réduire le coût pour les lecteurs de trouver un contenu de qualité?La réponse est:Quelqu'un que tu ne connais pas..
Il y a toujours des gens que tu ne connais pas,Savoir ce que vous voulez savoir.PaperWeekly Peut - être un pont,Promouvoir des contextes différents、Les universitaires et les inspirations académiques de différentes directions entrent en collision les uns avec les autres,Plus de possibilités.
PaperWeekly Encourager les laboratoires universitaires ou les particuliers,Partager des contenus de qualité sur notre plateforme,C'est possible.Interprétation du dernier article,C'est possible.Analyse des points chauds universitaires、Expérience scientifiqueOuExplication de l'expérience du concoursAttendez..Nous n'avons qu'un seul but.,Pour que la connaissance circule vraiment.
Exigences de base en matière de contributions:
• L'article est personnel.Travaux originaux,N'a pas été publié publiquement,Comme pour les articles publiés ou à publier sur d'autres plateformes,Veuillez indiquer clairement
• Les contributions proposées sont les suivantes: markdown Composition du format,Les dessins ci - joints sont envoyés en pièce jointe.,Image claire requise,Aucune question de droit d'auteur
• PaperWeekly Respect du droit d'auteur de l'auteur original,Et lancera chaque article original adopté,OffreRémunération concurrentielle des manuscrits dans l'industrie,Selon la quantité de lecture de l'article et la qualité de l'article, le règlement par étapes
Canal de contribution:
• Boîte aux lettres de contribution:[email protected]
• Veuillez noter vos coordonnées immédiates(Wechat),Afin que nous puissions contacter l'auteur dès que nous choisissons le manuscrit
• Vous pouvez également ajouter des tweets directement(pwbot02)Contributions rapides,Remarques:Nom-Contributions

△Appuyez longtemps pour ajouterPaperWeeklyPetit montage
Maintenant,In「Oui.」On peut aussi nous trouver
Recherche sur la page d'accueil「PaperWeekly」
Cliquez sur「Attention」Abonnez - vous à notre rubrique
·

边栏推荐
- [wechat applet] read the life cycle and route jump of the applet
- Embedded-c language-6
- Thoughtworks 全球CTO:按需求构建架构,过度工程只会“劳民伤财”
- mysql如何使用JSON_EXTRACT()取json值
- C#(Winform) 当前线程不在单线程单元中,因此无法实例化 ActiveX 控件
- Detailed explanation of printf() and scanf() functions of C language
- Redis+caffeine two-level cache enables smooth access speed
- [Jianzhi offer] 63 Maximum profit of stock
- 世界上最难的5种编程语言
- Practical example of propeller easydl: automatic scratch recognition of industrial parts
猜你喜欢
Embedded UC (UNIX System Advanced Programming) -2
Winedt common shortcut key modify shortcut key latex compile button
First day of learning C language
Rider set the highlighted side of the selected word, remove the warning and suggest highlighting
Summary of optimization scheme for implementing delay queue based on redis
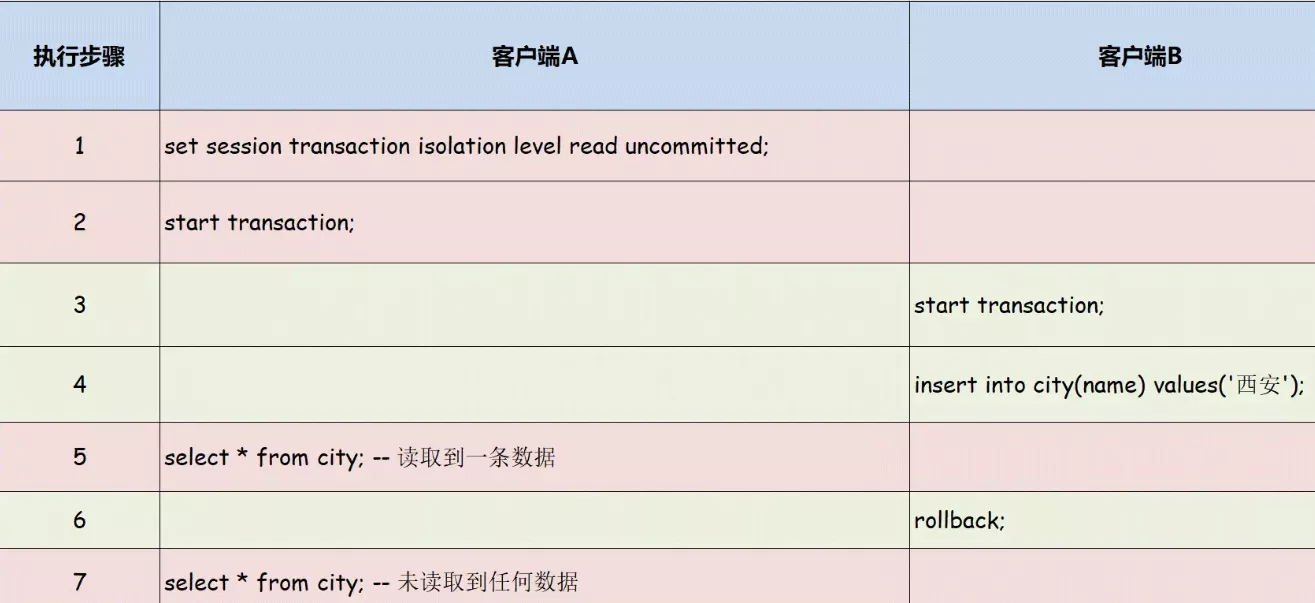
一文了解MySQL事务隔离级别

Embedded UC (UNIX System Advanced Programming) -1
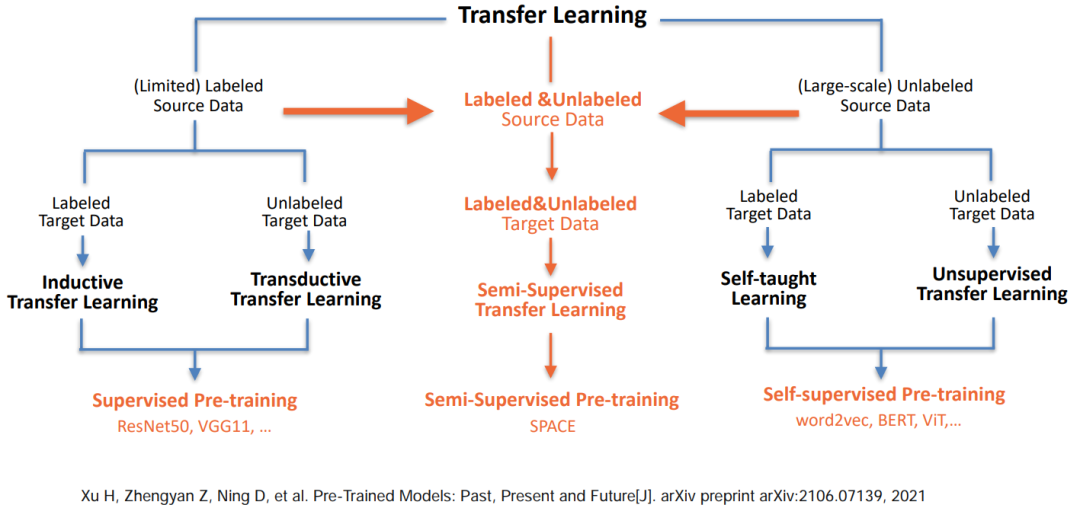
dried food! Semi supervised pre training dialogue model space
VBA驱动SAP GUI实现办公自动化(二):判断元素是否存在
腾讯音乐上线新产品“曲易买”,提供音乐商用版权授权
随机推荐
ClickHouse(03)ClickHouse怎么安装和部署
Alpha conversion from gamma space to linner space under URP (II) -- multi alpha map superposition
MYSQL group by 有哪些注意事项
【性能测试】jmeter+Grafana+influxdb部署实战
Cloud security daily 220705: the red hat PHP interpreter has found a vulnerability of executing arbitrary code, which needs to be upgraded as soon as possible
[first lecture on robot coordinate system]
What are the precautions for MySQL group by
C#实现水晶报表绑定数据并实现打印3-二维码条形码
网上办理期货开户安全吗?网上会不会骗子比较多?感觉不太靠谱?
flask解决CORS ERR 问题
Q2 encryption market investment and financing report in 2022: gamefi becomes an investment keyword
[Jianzhi offer] 63 Maximum profit of stock
Embedded UC (UNIX System Advanced Programming) -1
C # realizes crystal report binding data and printing 3-qr code barcode
一个满分的项目文档是如何书写的|得物技术
Embedded-c Language-5
IDC报告:腾讯云数据库稳居关系型数据库市场TOP 2!
漫画:寻找股票买入卖出的最佳时机
ICML 2022 | Meta提出鲁棒的多目标贝叶斯优化方法,有效应对输入噪声
Function sub file writing