当前位置:网站首页>Force deduction 62 different paths (the number of all paths from the upper left to the lower right of the matrix) (dynamic planning)
Force deduction 62 different paths (the number of all paths from the upper left to the lower right of the matrix) (dynamic planning)
2022-07-07 06:24:00 【Pei Nanwei_】
Today I come across a dynamic programming problem that I think is very valuable . From this question , I feel I have a deeper understanding of Dynamic Planning , You can see that it doesn't help you .
First look at the topic :
A robot is in a m x n The top left corner of the grid , The robot can only move down or right one step at a time . The robot tries to reach the lower right corner of the grid and asks how many different paths there are ?
Example
Input :m = 3, n = 2
Output :3
explain :
From the top left corner , All in all 3 Path to the bottom right .
1. towards the right -> Down -> Down
2. Down -> Down -> towards the right
3. Down -> towards the right -> Down
answer :
From the title , You can only move down or right at a time
From this we infer ===》 The number of paths to a grid , Determined by its left grid and upper grid
From this we infer ===》 Here we can use the idea of dynamic programming to solve
From this dynamic equation ===》 dp[i][j] = dp[i-1][j] + dp[i][j-1]
thus , We have solved half the problem , Then we think about the first column and the first row , Because you can only move down or right at a time , therefore Each grid in the first row can only be moved to the right from the grid on its left , So the first line dp[0][j] All for 1, The first column of lattice is the same .
This concludes the analysis , List codes
public int uniquePaths(int m, int n) {
int[][] dp = new int [m][n];
for(int i=0;i<n;i++){
dp[0][i] = 1;
}
for(int i=0;i<m;i++){
dp[i][0] = 1;
}
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
Okay , That's all for this article , Favorite students can like the collection , Have a problem , Can comment , Or leave a message , I will give you feedback at the first time , Thank you for watching. !!
notes : This article is for me to share my learning experience , There are mistakes or areas that need to be corrected , Please correct me. , I will accept with an open mind
边栏推荐
猜你喜欢
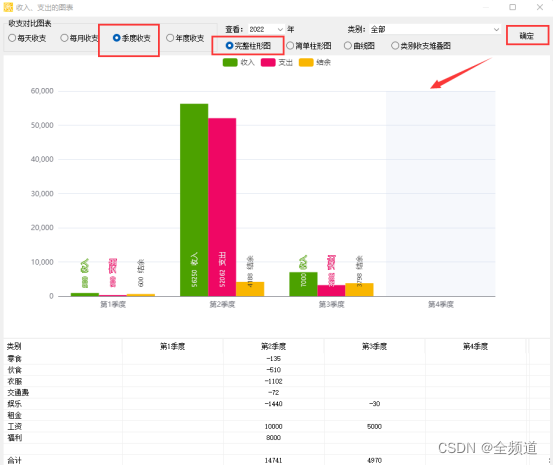
How to keep accounts of expenses in life

Markdown displays pictures side by side

Markdown 并排显示图片

港科大&MSRA新研究:关于图像到图像转换,Fine-tuning is all you need
![A freshman's summary of an ordinary student [I don't know whether we are stupid or crazy, but I know to run forward all the way]](/img/fd/7223d78fff54c574260ec0da5f41d5.png)
A freshman's summary of an ordinary student [I don't know whether we are stupid or crazy, but I know to run forward all the way]
POI导出Excel:设置字体、颜色、行高自适应、列宽自适应、锁住单元格、合并单元格...
Test the foundation of development, and teach you to prepare for a fully functional web platform environment

哈趣投影黑馬之姿,僅用半年强勢突圍千元投影儀市場!

面试中有哪些经典的数据库问题?
CloudCompare-点对选取
随机推荐
[shell] summary of common shell commands and test judgment statements
3531. Huffman tree
[SOC FPGA] peripheral PIO button lights up
Convert numbers to string strings (to_string()) convert strings to int sharp tools stoi();
How to solve sqlstate[hy000]: General error: 1364 field 'xxxxx' doesn't have a default value error
Calculation model FPS
On the discrimination of "fake death" state of STC single chip microcomputer
HKUST & MsrA new research: on image to image conversion, fine tuning is all you need
生活中的开销,怎么记账合适
3428. Put apples
力扣62 不同路径(从矩阵左上到右下的所有路径数量) (动态规划)
c面试 加密程序:由键盘输入明文,通过加密程序转换成密文并输出到屏幕上。
Redis(一)——初识Redis
一段程序让你明白什么静态内部类,局部内部类,匿名内部类
Symmetric binary tree [tree traversal]
骑士战胜魔王(背包&dp)
哈趣投影黑马之姿,仅用半年强势突围千元投影仪市场!
计算模型 FPS
PostgreSQL database timescaledb function time_ bucket_ Gapfill() error resolution and license replacement
FlexRay通信协议概述