当前位置:网站首页>容斥原理 AcWing 890. 能被整除的数
容斥原理 AcWing 890. 能被整除的数
2022-07-05 06:16:00 【T_Y_F666】
容斥原理 AcWing 890. 能被整除的数
原题链接
算法标签
容斥原理
思路
代码
#include<bits/stdc++.h>
#define int long long
#define abs fabs
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>=b;--i)
using namespace std;
const int N = 20;
int a[N];
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
void put(int x) {
if(x<0) putchar('-'),x=-x;
if(x>=10) put(x/10);
putchar(x%10^48);
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n=read(), m=read();
rep(i, 0, m){
a[i]=read();
}
int res=0;
// 枚举从1 到 1111...(m个1)的每一个集合状态, (至少选中一个集合)
rep(i, 1, 1<<m){
// t表示质数乘积 cnt表示当前选法集合数量
int t=1, cnt=0;
rep(j, 0, m){
if(i>>j&1){
// 乘积大于n, 则n/t = 0, 跳出这轮循环
if(t*a[j]>n){
t=-1;
break;
}
cnt++;
t*=a[j];
}
}
if(t!=-1){
if(cnt%2){
res+=n/t;
}else{
res-=n/t;
}
}
}
printf("%lld", res);
}
原创不易
转载请标明出处
如果对你有所帮助 别忘啦点赞支持哈
边栏推荐
- Appium foundation - use the first demo of appium
- A reason that is easy to be ignored when the printer is offline
- New title of module a of "PanYun Cup" secondary vocational network security skills competition
- 高斯消元 AcWing 884. 高斯消元解异或线性方程组
- SPI 详解
- [rust notes] 17 concurrent (Part 1)
- 实时时钟 (RTC)
- Erreur de connexion Navicat à la base de données Oracle Ora - 28547 ou Ora - 03135
- MySQL advanced part 2: SQL optimization
- Operator priority, one catch, no doubt
猜你喜欢
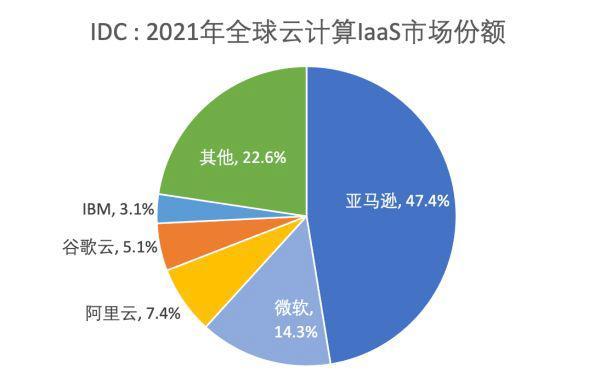
Quickly use Amazon memorydb and build your own redis memory database
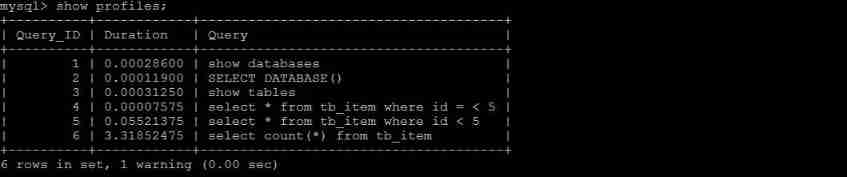
MySQL advanced part 2: optimizing SQL steps
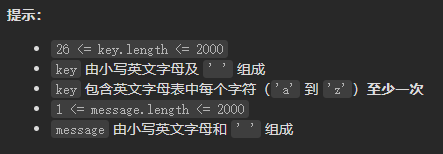
Leetcode-6108: decrypt messages
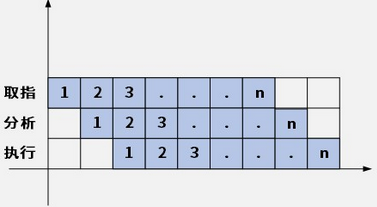
1.14 - 流水线

2021apmcm post game Summary - edge detection
SQL三种连接:内连接、外连接、交叉连接
LeetCode 0108. Convert an ordered array into a binary search tree - the median of the array is the root, and the left and right of the median are the left and right subtrees respectively

阿里新成员「瓴羊」正式亮相,由阿里副总裁朋新宇带队,集结多个核心部门技术团队

1.15 - 输入输出系统
Open source storage is so popular, why do we insist on self-development?
随机推荐
1.13 - RISC/CISC
Leetcode backtracking method
Leetcode-6109: number of people who know secrets
Is it impossible for lamda to wake up?
Leetcode array operation
LeetCode 0107.二叉树的层序遍历II - 另一种方法
LeetCode 1200. Minimum absolute difference
Daily question 1189 Maximum number of "balloons"
4. 对象映射 - Mapping.Mapster
TypeScript 基础讲解
Leetcode divide and conquer / dichotomy
SQLMAP使用教程(二)实战技巧一
Sword finger offer II 058: schedule
Record the process of configuring nccl and horovod in these two days (original)
LeetCode 0108. Convert an ordered array into a binary search tree - the median of the array is the root, and the left and right of the median are the left and right subtrees respectively
Data visualization chart summary (I)
Groupbykey() and reducebykey() and combinebykey() in spark
Leetcode-9: palindromes
【Rust 笔记】15-字符串与文本(下)
MySQL advanced part 2: optimizing SQL steps
