当前位置:网站首页>LeetCode 1984. Minimum difference in student scores
LeetCode 1984. Minimum difference in student scores
2022-07-06 16:43:00 【Daylight629】
1984. The minimum difference in student scores
To give you one Subscript from 0 Start Array of integers for nums , among nums[i] It means the first one i A student's grade . I'll give you another integer k .
Select any... From the array k A student's grade , Make this k Between scores The highest and Lowest score Of Difference value achieve To minimize the .
Return possible Minimum difference .
Example 1:
Input :nums = [90], k = 1
Output :0
explain : elect 1 A student's grade , have only 1 Methods :
- [90] The difference between the highest score and the lowest score is 90 - 90 = 0
The smallest possible difference is 0
Example 2:
Input :nums = [9,4,1,7], k = 2
Output :2
explain : elect 2 A student's grade , Yes 6 Methods :
- [9,4,1,7] The difference between the highest score and the lowest score is 9 - 4 = 5
- [9,4,1,7] The difference between the highest score and the lowest score is 9 - 1 = 8
- [9,4,1,7] The difference between the highest score and the lowest score is 9 - 7 = 2
- [9,4,1,7] The difference between the highest score and the lowest score is 4 - 1 = 3
- [9,4,1,7] The difference between the highest score and the lowest score is 7 - 4 = 3
- [9,4,1,7] The difference between the highest score and the lowest score is 7 - 1 = 6
The smallest possible difference is 2
Tips :
1 <= k <= nums.length <= 10000 <= nums[i] <= 105
Two 、 Method 1
Sort
class Solution {
public int minimumDifference(int[] nums, int k) {
int res = Integer.MAX_VALUE;
Arrays.sort(nums);
for (int i = 0; i + k - 1 < nums.length; i++) {
res = Math.min(res, nums[k + i - 1] - nums[i]);
}
return res;
}
}
Complexity analysis
Time complexity :O(nlogn), among n It's an array nums The length of . The time required for sorting is O(nlogn), The time required for subsequent traversal is O(n).
Spatial complexity :O(logn), This is the stack space needed for sorting .
边栏推荐
- SQL快速入门
- Sublime text code formatting operation
- Use JQ to realize the reverse selection of all and no selection at all - Feng Hao's blog
- (lightoj - 1369) answering queries (thinking)
- Problem - 922D、Robot Vacuum Cleaner - Codeforces
- ByteDance new programmer's growth secret: those glittering treasures mentors
- QT implementation window gradually disappears qpropertyanimation+ progress bar
- 业务系统从Oracle迁移到openGauss数据库的简单记录
- 软通乐学-js求字符串中字符串当中那个字符出现的次数多 -冯浩的博客
- Market trend report, technical innovation and market forecast of double-sided foam tape in China
猜你喜欢
MariaDB的安装与配置
js封装数组反转的方法--冯浩的博客
Problem - 922D、Robot Vacuum Cleaner - Codeforces

It is forbidden to trigger onchange in antd upload beforeupload
Local visualization tools are connected to redis of Alibaba cloud CentOS server
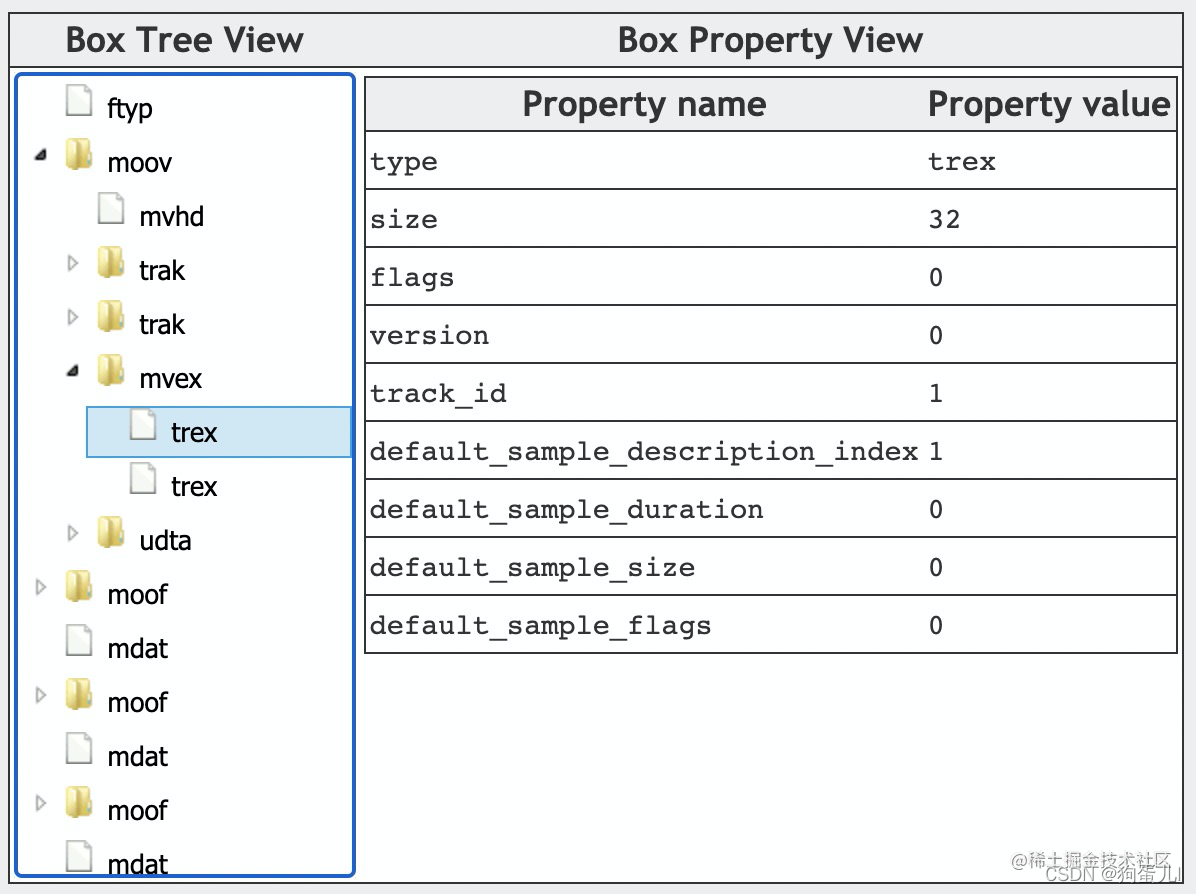
Mp4 format details
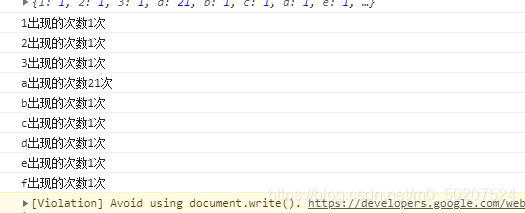
Soft music -js find the number of times that character appears in the string - Feng Hao's blog
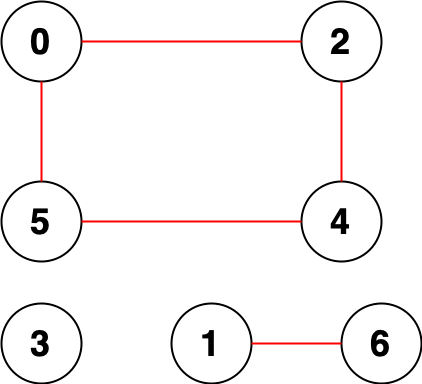
Li Kou: the 81st biweekly match
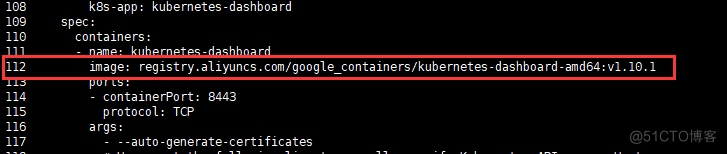
Kubernetes集群部署
Chapter 2 shell operation of hfds
随机推荐
MariaDB的安装与配置
Spark的RDD(弹性分布式数据集)返回大结果集
Spark独立集群动态上线下线Worker节点
Basic principles of video compression coding and audio compression coding
Codeforces Round #771 (Div. 2)
antd upload beforeUpload中禁止触发onchange
提交Spark应用的若干问题记录(sparklauncher with cluster deploy mode)
Hbuilder x format shortcut key settings
Log statistics (double pointer)
Business system compatible database oracle/postgresql (opengauss) /mysql Trivia
图像处理一百题(1-10)
两个礼拜速成软考中级软件设计师经验
Codeforces Round #800 (Div. 2)AC
Sublime text code formatting operation
Local visualization tools are connected to redis of Alibaba cloud CentOS server
指定格式时间,月份天数前补零
(lightoj - 1369) answering queries (thinking)
图像处理一百题(11-20)
Investigation report of bench type Brinell hardness tester industry - market status analysis and development prospect prediction
视频压缩编码和音频压缩编码基本原理