当前位置:网站首页>顺丰科技智慧物流校园技术挑战赛(无t4)
顺丰科技智慧物流校园技术挑战赛(无t4)
2022-07-06 09:28:00 【你好_Ä】
顺丰科技智慧物流校园技术挑战赛(无t4)
顺丰鄂州枢纽运转中心环线检测 - 力扣 (LeetCode) 竞赛
【背景】
鄂州花湖机场是亚洲第一个、世界第四个专业货运枢纽机场。2016年4月获中国民用航空局正式批复,2017年12月20日枢纽工程正式开工,2022年3月19日由顺丰航空使用波音B757-200F型全货机执行试飞成功,系中国首次以全货机机型完成新机场的试飞工作。
顺丰鄂州枢纽转运中心占地约百万平方,实现了快件从卸载(卸车/卸机)到分拣再到装车/打板全自动化。自动化设备运输线总长超过数十公里。如何保障快件最高效到达装车或打板口是核心需要解决的问题。
转运中心内自动化设备通过运输线连接,构成一张立体的连通网络,快件达到分流路口需要决策行走支路,确保全程线路最优前提下,同时要避免大量快件涌向最短线路造成拥堵,还需要及时避开故障线路上的故障设备,直到故障得到修复。
自动化运输线简化图如下:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cGS5Wk2t-1655727366330)(https://pic.leetcode-cn.com/1652078050-dkDCol-探客-有向图 (6)].png)
卸载口代表快件行走起始节点,装载口代表快件经过路线行走后最终目的节点,节点代表从卸载口到达装载口途径线路的分流或汇流点,卸载口和装载口也是一种特殊的节点。
边代表两个相邻节点间自动化设备运输线,线路代表从起始节点到达目的节点(装载口)途径所有的边。
在整连通网络上不应该存在环形线路,环形线路可能会导致快件在运输线上长时间运输,以至于错过飞机或车辆班次,导致延误。因此在建立线路数据模型时应避免出现环。
【问题】
请帮忙检测线路上是否存在环形通路。
示例 1:
输入:
"1->2,2->3,3->1"输出:
true
提示:
- 0 < 节点数 < 100
问题解析
数据量小的可怜。
把所有路径都记录好后,以每一个点为起点进行dfs,如果在一次dfs中能到达一个点两次就说明存在通路。
AC代码
class Solution {
public:
unordered_map<int,vector<int>>mymap;
unordered_map<int,int>cnt;
bool dfs(int x)
{
if(cnt[x]==1)return true;
cnt[x]=1;
for(auto i:mymap[x])
{
if(dfs(i))return true;
}
cnt[x]=0;
return false;
}
bool hasCycle(string graph) {
int n=graph.size();
for(int i=0;i<n;i++)
{
int a=0,b=0;
while(i<n&&graph[i]>='0'&&graph[i]<='9')
{
a*=10;
a+=(graph[i]-'0');
i++;
}
i+=2;
while(i<n&&graph[i]>='0'&&graph[i]<='9')
{
b*=10;
b+=(graph[i]-'0');
i++;
}
mymap[a].push_back(b);
}
bool flag=false;
for(int i=1;i<=100;i++)
{
if(dfs(i))return true;
}
return false;
}
};
小哥派件装载问题 - 力扣 (LeetCode) 竞赛
问题
快递小哥每天都需要揽件并骑电瓶车派送快递,假设电瓶车快递箱容量为V,小哥需要派送n个快递,每个快递都有一定的体积大小。
要求在需要派送的n个快递中,任取若干个快递装放入快递箱,不能溢出,使快递箱的剩余空间最小。
输入:
- n个快递的体积数组:N[],
- 电瓶车快递箱容量:V
返回:
- 尽量装满快递后,快递箱剩余的最小容量
示例1
输入:N = [8, 1, 12, 7, 9, 7], V = 11
输出:1
解释:快递箱容量V为11,物品体积数组N为[8, 1, 12, 7, 9, 7],最优解为取体积为
1的快递和体积为9的快递,即快递箱剩余最小空间为 11-(1+9)=1
提示
- 0 < N.length ≤ 30
- 0 < N[i] < 2000
- V为整数:0 ≤ V ≤ 2000
问题解析
01背包模板题,先求体积V能拿的最多货物,最后返回背包体积V和拿的货物的差值就行。
AC代码
class Solution {
public:
int minRemainingSpace(vector<int>& N, int V) {
int n=N.size();
vector<int>f(V+1);
for(int i=0;i<n;i++)
{
for(int j=V;j>=N[i];j--)
{
f[j]=max(f[j],f[j-N[i]]+N[i]);
}
}
return V-f[V];
}
};
收件节节高 - 力扣 (LeetCode) 竞赛
背景
夏天就来了,天气越来越热了,顺丰小哥收派快递非常辛苦。为了鼓励小哥,我们设置了各种有奖竞赛活动。这其中就有一个叫收件节节高的竞赛,该竞赛比较的是小哥日收件数连续增长的天数,连续增长天数越大排名越高。
问题
小哥人数较多,请帮忙设计一个可以快速算出小哥日收件最大连续增长天数的算法。
输入: 一维数组nums[n]
输出: 连续递增天数长度
示例:
输入:[54,42,62,75,82,86,86]
输出:5
解释:
小哥A最近一周的收件数分别是:54,42,62,75,82,86,86,那么小哥A在这周的日收件最大连续增长天数是5
- 小哥A在这周第2天开始到第6天的日收件数都是在增长
- 第7天与第6天收件数一样,不算增长
提示:
- 0 <= nums.length < 200000
问题解析
用dp[i]表示到第i天时连续增长的天数,判断当前元素是否大于上个元素,如果大于:dp[i]=dp[i-1]+1,如果不等于:dp[i]=1;在此过程中维护最大值即可。
AC代码
class Solution {
public:
int findMaxCI(vector<int>& nums) {
int n=nums.size();
vector<int>f(n,1);
int res=1;
for(int i=1;i<n;i++)
{
if(nums[i]>nums[i-1])f[i]+=f[i-1];
res=max(f[i],res);
}
return res;
}
};
顺丰中转场车辆入场识别-电子围栏 - 力扣 (LeetCode) 竞赛
就是判断一个点在不在多边形里,网上一搜一大把
慧眼神瞳 - 力扣 (LeetCode) 竞赛
【背景】
"慧眼神瞳"平台可以通过分析摄像头监控画面,进行自动化的识别场地形象是否符合标准、工具是否定置定位、火灾预警、防盗预警、异常人员入侵预警等情况。
出于运维考虑,要求场地对摄像头进行分组管理,每组有专门的负责人负责管理。
【问题】
假设平台部署摄像头的距离集合distance,为场地安排n个负责人,其中:
distance[i][j]表示摄像头i和摄像头j之间的距离,如果distance[i][j]<=2米说明它们属于同一组。
请你设计一个算法判断该场地是否可以保证每组摄像头至少有一个负责人管理。
输入: 摄像头部署之间距离集合m*m的二维数组distance[m][m],人员数量n
输出:是否满足要求的结果:true/false
示例1:
假设存在三个摄像头1,2,3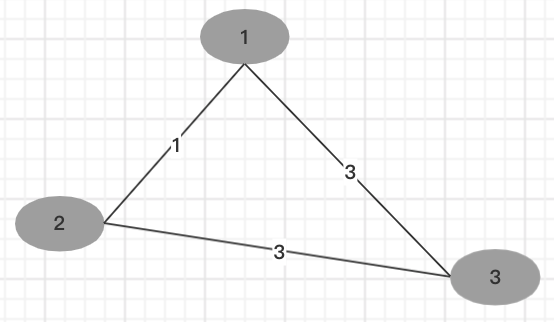
输入:distance=[[0,1,3], [1,0,3], [3,3,0]], n = 2
输出:true
解释:
distance:摄像头部署之间距离集合,摄像头id=索引i+1;
distance=[
[0,1,3], => 摄像头id1(i=0)分别到摄像头id1、2、3(j=0,1,2)的距离:id1->id1: 0米;id1->id2: 1米;id1->id3: 3米
[1,0,3], => 摄像头id2(i=1)分别到摄像头id1、2、3(j=0,1,2)的距离:id2->id1: 1米;id2->id2: 0米;id2->id3: 3米
[3,3,0]] => 摄像头id3(i=2)分别到摄像头id1、2、3(j=0,1,2)的距离:id3->id1: 3米;id3->id2: 1米;id3->id3: 3米
n:负责人个数
摄像头1与2的距离为1,摄像头1与3的距离为3,摄像头2与3的距离为3,所以摄像头1和2为一组,摄像头3自己一组,一共有2组摄像头,2<=n,所以能够满足每组至少有一个负责人管理。
问题解析
dfs或是直接上并查集都行,把所有路径小于等于2的都看为一个连通块,看有多少个联通块即可。
我用dfs,以每个点为起点进行dfs,把每次遍历到的路径距离小于等于2的点都打上标记,每次以一个点为起点进行dfs则计数器++,如果这个起点在之前的dfs就遇到过则不进行dfs。最后返回计数器即可。
AC代码
class Solution {
public:
unordered_map<int,int>mymap;
void dfs(int x,vector<vector<int>>& distance)
{
if(mymap[x]==1)return ;
mymap[x]=1;
int n=distance[x-1].size();
for(int i=0;i<n;i++)
{
if(distance[x-1][i]<=2)
dfs(i+1,distance);
}
}
bool isCompliance(vector<vector<int>>& distance, int n) {
int len=distance.size(),res=0;
for(int i=0;i<len;i++)
{
if(mymap[i+1]==0)
{
res++;
dfs(i+1,distance);
}
}
return res<=n;
}
};
边栏推荐
猜你喜欢
![[exercise-4] (UVA 11988) broken keyboard = = (linked list)](/img/59/78ca7170ab1fd364ec44cfbcdc7ab5.png)
[exercise-4] (UVA 11988) broken keyboard = = (linked list)
第 300 场周赛 - 力扣(LeetCode)
“鬼鬼祟祟的”新小行星将在本周安全掠过地球:如何观看
Gartner: five suggestions on best practices for zero trust network access
b站 實時彈幕和曆史彈幕 Protobuf 格式解析
渗透测试 2 --- XSS、CSRF、文件上传、文件包含、反序列化漏洞
Penetration test (8) -- official document of burp Suite Pro
Ball Dropping
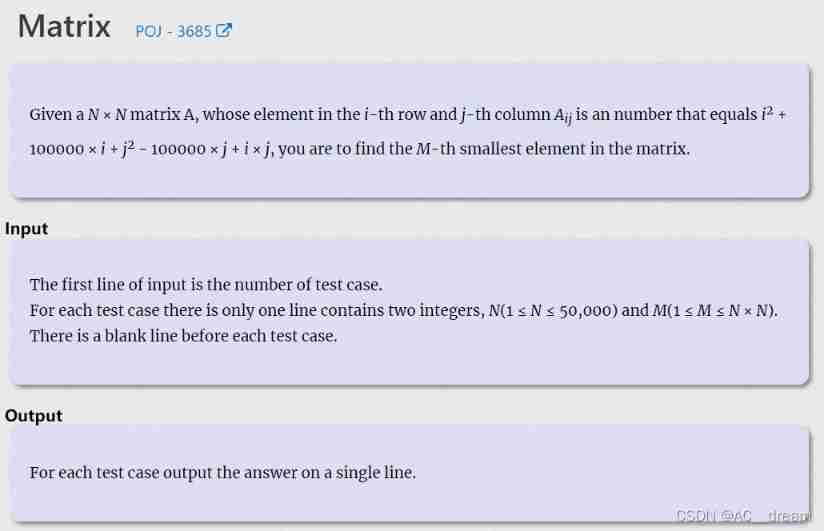
(POJ - 3685) matrix (two sets and two parts)
滲透測試 ( 1 ) --- 必備 工具、導航
随机推荐
Vs2019 initial use
Socket communication
1605. Sum the feasible matrix for a given row and column
(POJ - 3258) River hopper (two points)
树莓派4B安装opencv3.4.0
The most complete programming language online API document
[exercise-7] (UVA 10976) fractions again?! (fraction split)
Quick to typescript Guide
875. 爱吃香蕉的珂珂 - 力扣(LeetCode)
AcWing:第56场周赛
860. Lemonade change
Openwrt build Hello ipk
Penetration test (3) -- Metasploit framework (MSF)
[exercise-1] (UVA 673) parentheses balance/ balanced brackets (stack)
[exercise-8] (UVA 246) 10-20-30== simulation
New to redis
window11 conda安装pytorch过程中遇到的一些问题
MySQL grants the user the operation permission of the specified content
浏览器打印边距,默认/无边距,占满1页A4
双向链表—全部操作