当前位置:网站首页>机械臂速成小指南(十):可达工作空间
机械臂速成小指南(十):可达工作空间
2022-07-06 21:16:00 【躺躺我啊】
指南目录:
********************以下为正文********************
在指南(九)中,我们已得到六自由度机械臂的正运动学方程,将关节变量代入该方程即可求得机械臂末端的位姿。现在我们已经知道了每个关节的可旋转的范围,那么,我们同时也可以得到机械臂末端所能到达的所有位置,我们将这个可能到达的位置的集合称为可达工作空间,而这也是机械臂的一个重要参数指标。
指南中使用使用MATLAB中的Robotic Toolbox工具箱(不是官方的Robotics System Toolbox )对机械臂进行运动学仿真,并使用易于实现且运行速度快的蒙特卡洛方法得到机械臂的可达工作空间。

一、关节空间与驱动器空间
关节空间描述与驱动器空间描述是两种用于描述机械臂位姿的方法。
1.关节空间
对于一个具有n个自由度的机械臂来说,它所有连杆的位置可由一组n个关节变量加以确
定。这样的一组变量常被称为nx1的关节矢量。所有关节矢量组成的空间称为关节空间。
2.驱动器空间
到目前为止,我们一直假设每个关节都是直接由某种驱动器驱动。然而,对于许多工业机器人来说并非如此,有时我们也会使用两个驱动器以差动的方式驱动一个关节,有时又会用直线驱动器通过四连杆机构来驱动旋转关节。
在这些情况下,就需要考虑驱动器空间。由于测量机械臂关节变化的传感器通常安装于驱动器上,因此进行某些计算时必须把关节矢量表示成一组驱动器函数,即驱动器矢量。所有驱动器矢量组成的空间称为驱动器空间。
二、工作空间(workspace)
工作空间(workspace)是当机械臂的所有关节进行所有可能的运动时,末端执行器坐标系的原点位置的集合。工作空间可分为为可达(reachable)工作空间与灵活(dexterous)工作空间。
工作空间是有限、闭合、连贯的。因为关节是转动型或移动型的,易知到工作空间是由平面、球形、环形和圆柱形等曲面元素组成的。机械臂厂商都会在数据手册中以俯视图和平视图的形式给出机械臂的工作空间,是用于评估机器人在预期应用中的性能所需的基本要素。
1.可达工作空间
机械臂末端执行器以一种以上的方向到达的目标点的集合为可达工作空间。
2.灵活工作空间
机械臂能以任意方向到达的目标点的集合为灵活工作空间。
3.机械臂可达工作空间计算的编程实现
%蒙特卡洛法仿真机械臂可达工作空间
%刘躺
radian1 = pi/180;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%定义DH参数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%刘躺%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
d1 = 169.77;
d2 = 0;
d3 = 0;
d4 = -222.63;
d5 = 0;
d6 = -36.25;
%机械臂连杆长度参数a
a1 = 64.2;
a2 = 305;
a3 = 0;
a4 = 0;
a5 = 0;
a6 = 0;
%机械臂关节偏角参数alpha
alpha1 = -90 * radian1;
alpha2 = 0 * radian1;
alpha3 = 90 * radian1;
alpha4 = -90 * radian1;
alpha5 = 90 * radian1;
alpha6 = 0 * radian1;
%定义关节角度限制
lim1_min = -170 * radian1; lim1_max = 170 * radian1; %关节1(-170,170)
lim2_min = -132 * radian1; lim2_max = 0 * radian1; %关节2(-132,0)
lim3_min = 1 * radian1; lim3_max = 141 * radian1; %关节3(1,141)
lim4_min = -165 * radian1; lim4_max = 165 * radian1; %关节4(-165,165)
lim5_min = -105 * radian1; lim5_max = 105 * radian1; %关节5(-105,105)
lim6_min = -155 * radian1; lim6_max = 155 * radian1; %关节6(-155,155)
%定义关节旋转范围
lim1 = lim1_max - lim1_min;
lim2 = lim2_max - lim2_min;
lim3 = lim3_max - lim3_min;
lim4 = lim4_max - lim4_min;
lim5 = lim5_max - lim5_min;
lim6 = lim6_max - lim6_min;
% 定义各个连杆以及关节类型,默认为转动关节
% θ d a α 角度限制 关节偏置
L(1)=Link([ 0 d1 a1 alpha1]); L(1).qlim=[lim1_min,lim1_max];
L(2)=Link([ 0 d2 a2 alpha2]); L(2).qlim=[lim2_min,lim2_max];
L(3)=Link([ 0 d3 a3 alpha3]); L(3).qlim=[lim3_min,lim3_max]; L(3).offset=-pi/2;
L(4)=Link([ 0 d4 a4 alpha4]); L(4).qlim=[lim4_min,lim4_max];
L(5)=Link([ 0 d5 a5 alpha5]); L(5).qlim=[lim5_min,lim5_max];
L(6)=Link([ 0 d6 a6 alpha6]); L(6).qlim=[lim6_min,lim6_max]; L(6).offset=pi;
%组合上述连杆
AR3=SerialLink(L,'name','AR3');
%显示机械臂关节数以及D_H参数列表
%AR3:: 6 axis, RRRRRR, stdDH, slowRNE
AR3.display();
%使用蒙特卡洛法绘制机械臂的工作空间
N=15000;
theta1 = ( lim1_min + (lim1 * rand(N,1)) );
theta2 = ( lim2_min + (lim2 * rand(N,1)) );
theta3 = ( lim3_min + (lim3 * rand(N,1)) );
theta4 = ( lim4_min + (lim4 * rand(N,1)) );
theta5 = ( lim5_min + (lim5 * rand(N,1)) );
theta6 = ( lim6_min + (lim6 * rand(N,1)) );
for n = 1:N
theta = [theta1(n),theta2(n),theta3(n),theta4(n),theta5(n),theta6(n)];
workspace = AR3.fkine(theta);
plot3(workspace.t(1),workspace.t(2),workspace.t(3),'b.','markersize',1);
hold on;
end
AR3.plot(theta); %动画显示
%进行机器人的实时展示
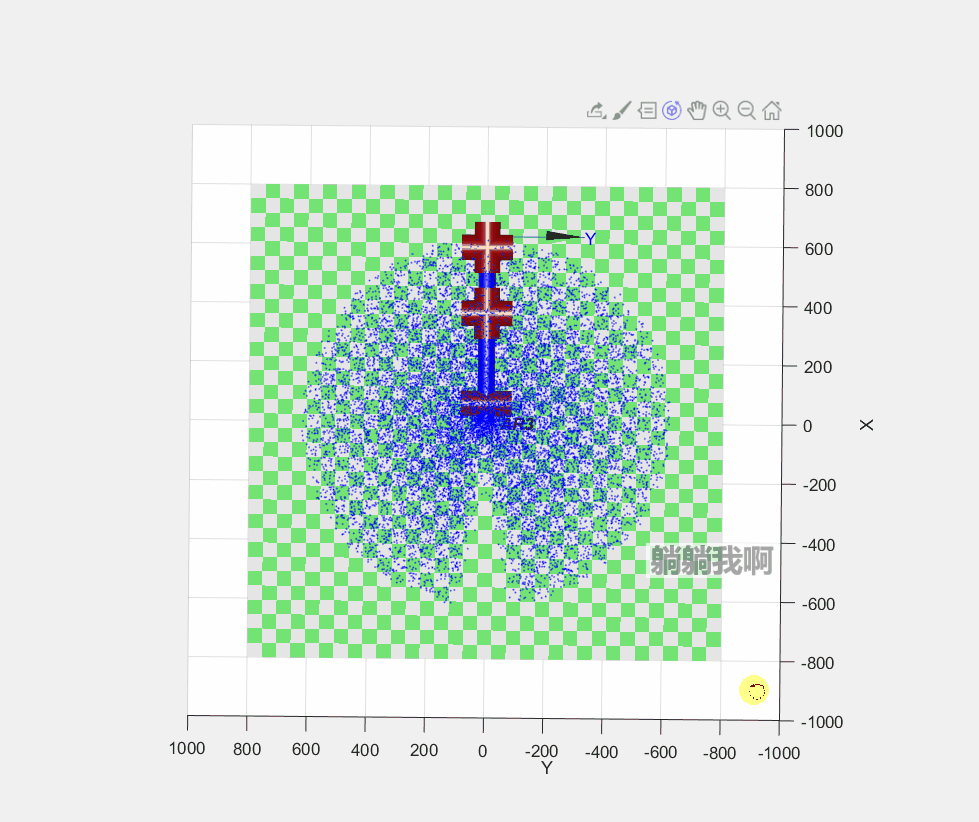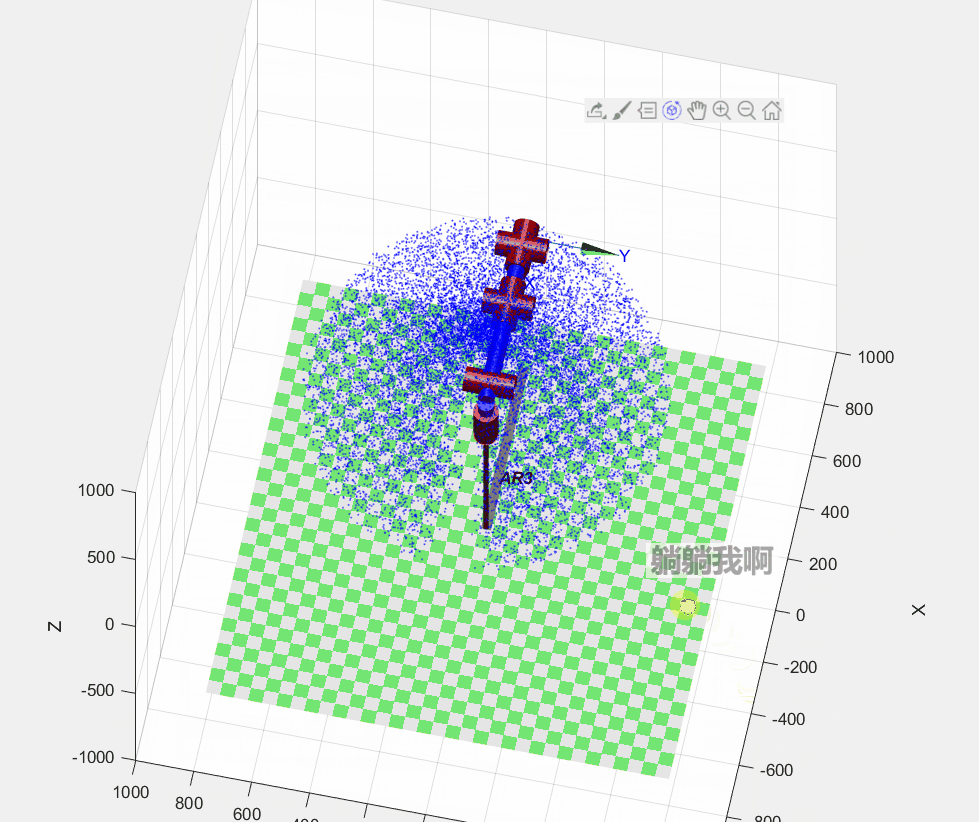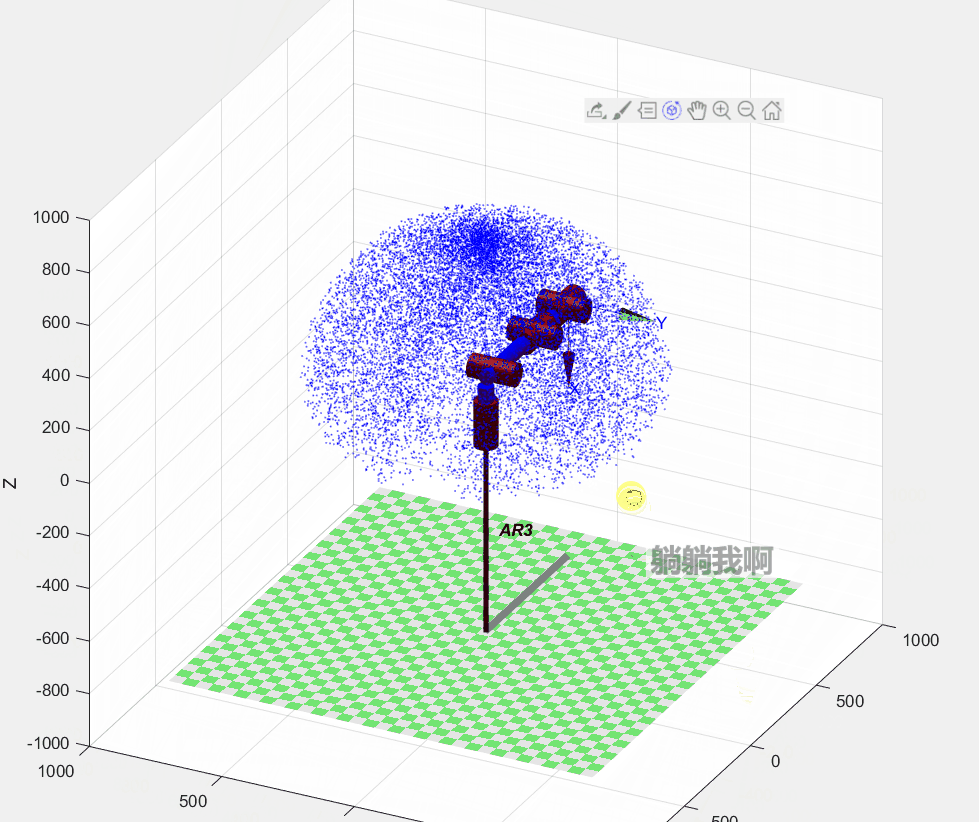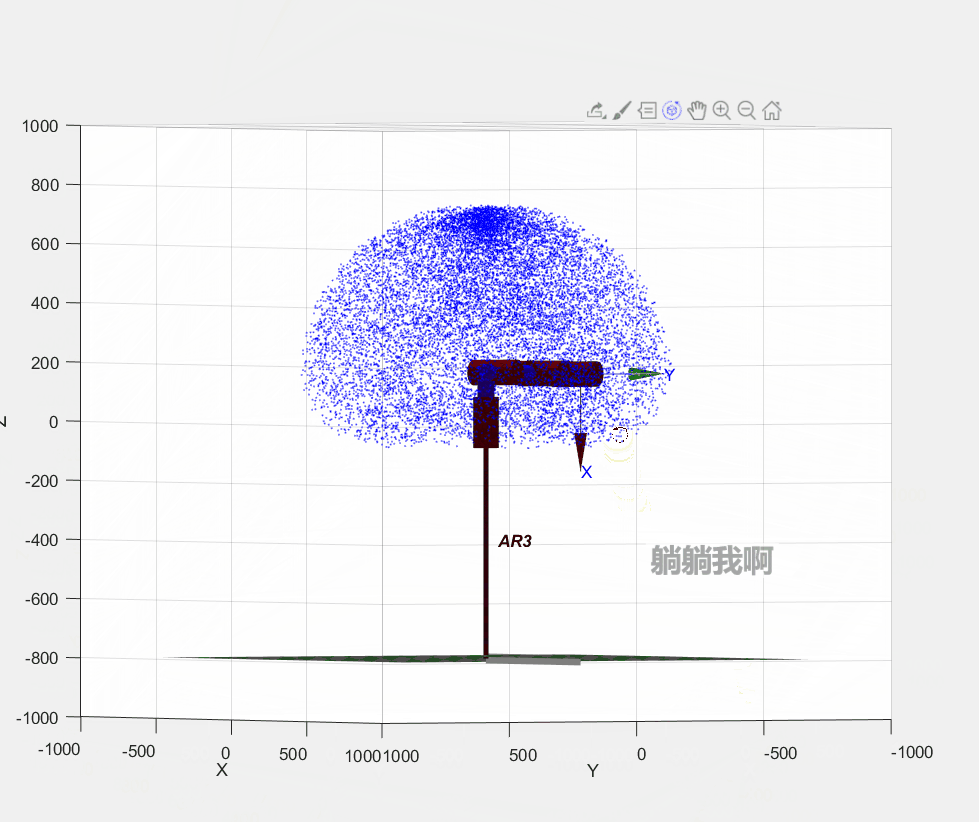
AR3.teach();具体编程过程为:首先根据上一章节中所定义的机械臂运动学参数对Robotic Toolbox工具箱中机械臂相关参数赋值,以此构建机械臂的仿真模型;接着,生成30000个随机关节变量,依次代入正运动学方程进行求解;最后,将代表末端执行器可达位置的点标注于三维空间中,形成的点阵即可表示机械臂的可达工作空间,程序运行效果如下图所示。
 |  | 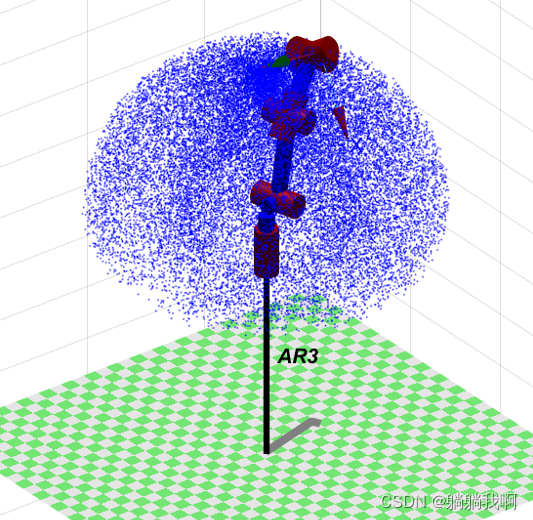 |
边栏推荐
- Kotlin Android 环境搭建
- When QT uses qtooltip mouse to display text, the picture of the button will also be displayed and the prompt text style will be modified
- Delete data in SQL
- 小程序能运行在自有App中,且实现直播和连麦?
- Preprocessing - interpolation
- QT 打开文件 使用 QFileDialog 获取文件名称、内容等
- 一些常用软件相关
- Docker部署Mysql8的实现步骤
- tflite模型转换和量化
- QT thread and other 01 concepts
猜你喜欢
Do you choose pandas or SQL for the top 1 of data analysis in your mind?
你心目中的数据分析 Top 1 选 Pandas 还是选 SQL?

QT item table new column name setting requirement exercise (find the number and maximum value of the array disappear)
链表面试常见题
未来发展路线确认!数字经济、数字化转型、数据...这次会议很重要

List interview common questions
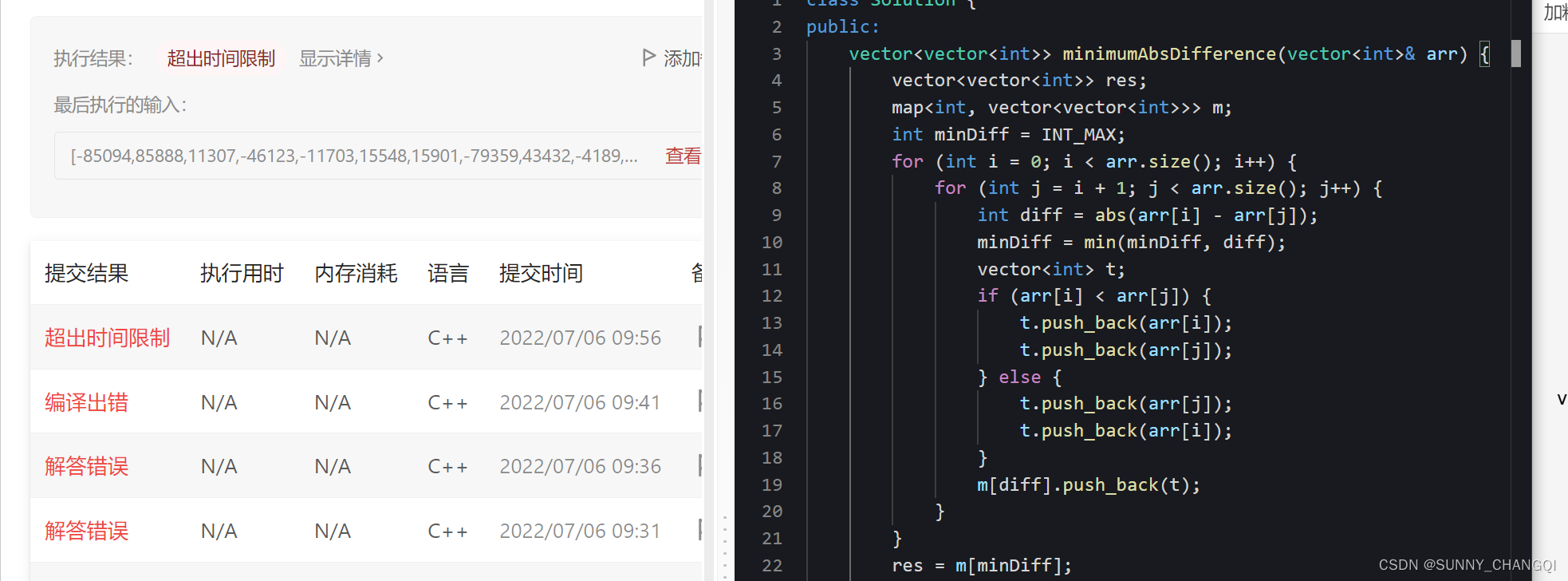
1200.Minimum Absolute Difference

维护万星开源向量数据库是什么体验
QT opens a file and uses QFileDialog to obtain the file name, content, etc
![[security attack and Defense] how much do you know about serialization and deserialization?](/img/1c/e5ae74e65bacf688d7f61cc1b71d3e.png)
[security attack and Defense] how much do you know about serialization and deserialization?
随机推荐
NoSQL之Redis配置与优化
HW notes (II)
MySQL storage engine
QT 项目 表格新建列名称设置 需求练习(找数组消失的数字、最大值)
List interview common questions
25. (ArcGIS API for JS) ArcGIS API for JS line modification line editing (sketchviewmodel)
Huawei and Xiaomi "copy each other"
Probability formula
Construction of Hisilicon universal platform: color space conversion YUV2RGB
SSL certificate deployment
Native MySQL
Class常量池与运行时常量池
哈夫曼树基本概念
When QT uses qtooltip mouse to display text, the picture of the button will also be displayed and the prompt text style will be modified
我的勇敢对线之路--详细阐述,浏览器输入URL发生了什么
使用 BR 备份 TiDB 集群到 GCS
24. (ArcGIS API for JS) ArcGIS API for JS point modification point editing (sketchviewmodel)
Top 50 hit industry in the first half of 2022
Search of linear table
MySQL的索引