After reading this article , You can go and get the following questions :
1143. Longest common subsequence
-----------
Longest common subsequence (Longest Common Subsequence, abbreviation LCS) Is a very classic interview topic , Because its solution is a typical two-dimensional dynamic programming , Most of the more difficult string problems are similar to this problem , For example, editing distance . and , This algorithm can be used to solve other problems with a little modification , So LCS The algorithm is worth learning .
The title is to let us find two strings of LCS length :
Input : str1 = "abcde", str2 = "ace"
Output : 3
explain : The longest common subsequence is "ace", Its length is 3
There must be readers who will ask , Why is this problem solved by dynamic programming ? Because of the type of subsequence , It's not easy to enumerate all possible outcomes , And the dynamic programming algorithm is exhaustive + prune , They're made for each other . So it can be said that as long as the subsequence problem is involved , Nine times out of ten, dynamic planning is needed to solve , It's right to think about this .
Now let's analyze it by hand , How to solve this problem with dynamic programming techniques .
One 、 Dynamic planning ideas
First step , Be clear dp The meaning of array . For the dynamic programming of two strings , The routine is universal .
For example, for Strings s1 and s2, Generally speaking, it is necessary to construct such a DP table:
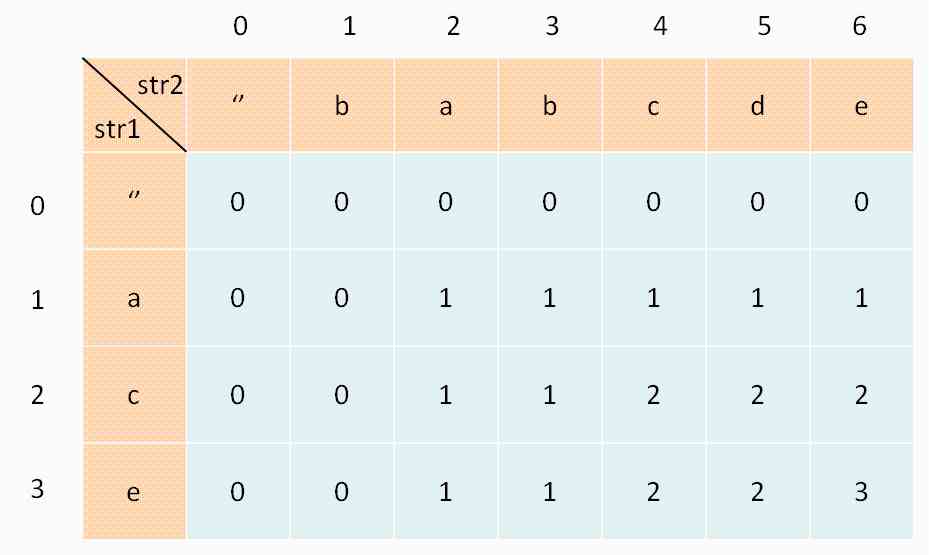
For the convenience of understanding this table , For the time being, we think the index is from 1 At the beginning , Just make a little adjustment in the code later . among ,dp[i][j] The meaning is : about s1[1..i] and s2[1..j], Their LCS The length is dp[i][j].
For example, in the example above ,d[2][4] That means : about "ac" and "babc", Their LCS The length is 2. The final answer we want to get is dp[3][6].
The second step , Definition base case.
We've got the index to be 0 Rows and empty columns ,dp[0][..] and dp[..][0] Should be initialized to 0, This is it. base case.
for instance , According to just now dp Definition of array ,dp[0][3]=0 The meaning is : For strings "" and "bab", Its LCS The length of is 0. Because a string is empty , The length of their longest common subsequence should obviously be 0.
The third step , Find the state transition equation .
This is the most difficult step in dynamic planning , Fortunately, this string problem has the same pattern , Let's talk about the way to deal with this kind of problem .
State transition is simply about making choices , Let's say this question , Is to seek s1 and s2 The longest common subsequence of , Let's call this subsequence lcs. So for s1 and s2 Each character in , What's the choice ? It's simple , Two options , Either in lcs in , Or not .
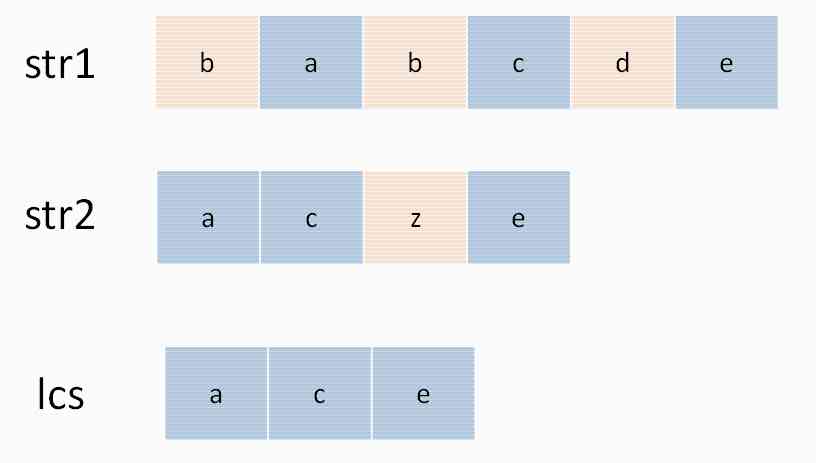
This 「 stay 」 and 「 be not in 」 Is to choose , The key is , How to choose ? This needs a little brain work : If a character should be in lcs in , So this character must exist at the same time s1 and s2 in , because lcs It's the longest public Subsequences . So the idea of this question is like this :
With two Pointers i and j Go back and forth s1 and s2, If s1[i]==s2[j], So this character It must be lcs in ; Otherwise ,s1[i] and s2[j] These two characters At least one of them is not here lcs in , One needs to be discarded . Let's take a look at recursion , Easier to understand :
def longestCommonSubsequence(str1, str2) -> int:
def dp(i, j):
# Empty string of base case
if i == -1 or j == -1:
return 0
if str1[i] == str2[j]:
# I found one here lcs The elements of , Keep looking for
return dp(i - 1, j - 1) + 1
else:
# Who can make lcs The longest , Just listen to who
return max(dp(i-1, j), dp(i, j-1))
# i and j Initialize to the last index
return dp(len(str1)-1, len(str2)-1)
For the first case , Find one lcs The characters in , At the same time i j Move one bit forward , And give lcs Add one... To the length of ; For the latter , Then try two situations , Take a bigger result .
PS: I've seriously written about 100 Multiple original articles , Hand brush 200 Daoli is the subject , All published in labuladong A copy of the algorithm , Continuous updating . Recommended collection , Write the title in the order of my article , Master all kinds of algorithm set, then put into the sea of questions, like fish .
In fact, this code is a brute force solution , We can go through memos or DP table To optimize time complexity , For example, as described above DP table To solve :
def longestCommonSubsequence(str1, str2) -> int:
m, n = len(str1), len(str2)
# structure DP table and base case
dp = [[0] * (n + 1) for _ in range(m + 1)]
# Make a state transition
for i in range(1, m + 1):
for j in range(1, n + 1):
if str1[i - 1] == str2[j - 1]:
# Find one lcs The characters in
dp[i][j] = 1 + dp[i-1][j-1]
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[-1][-1]
Two 、 Troubleshooting
about s1[i] and s2[j] Unequal situation , At least one The character is not in lcs in , Is it possible that neither character is there ? For example, the following situation :
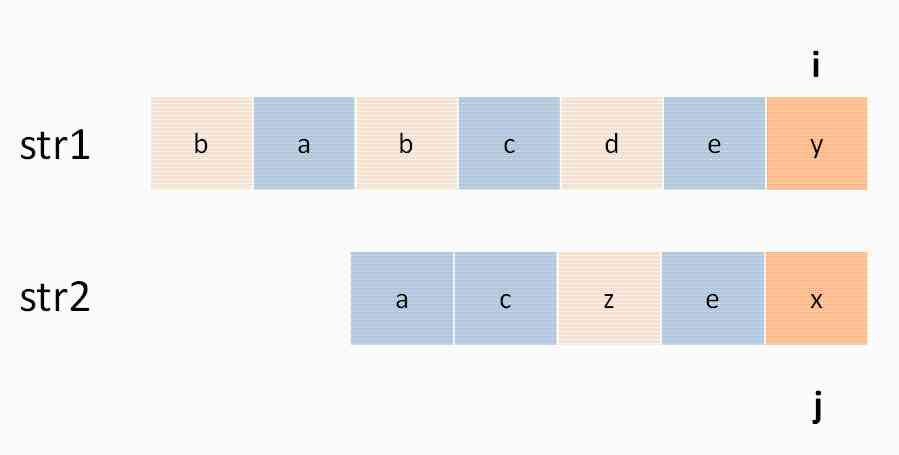
So whether the code should consider this situation , To such :
if str1[i - 1] == str2[j - 1]:
# ...
else:
dp[i][j] = max(dp[i-1][j],
dp[i][j-1],
dp[i-1][j-1])
I had this suspicion at the beginning , In fact, it can be changed in this way , You can also get the right answer , But it's unnecessary , because dp[i-1][j-1] Always the smallest of the three ,max It's impossible to get it at all .
The reason is that we are very concerned about dp Definition of array : about s1[1..i] and s2[1..j], Their LCS The length is dp[i][j].
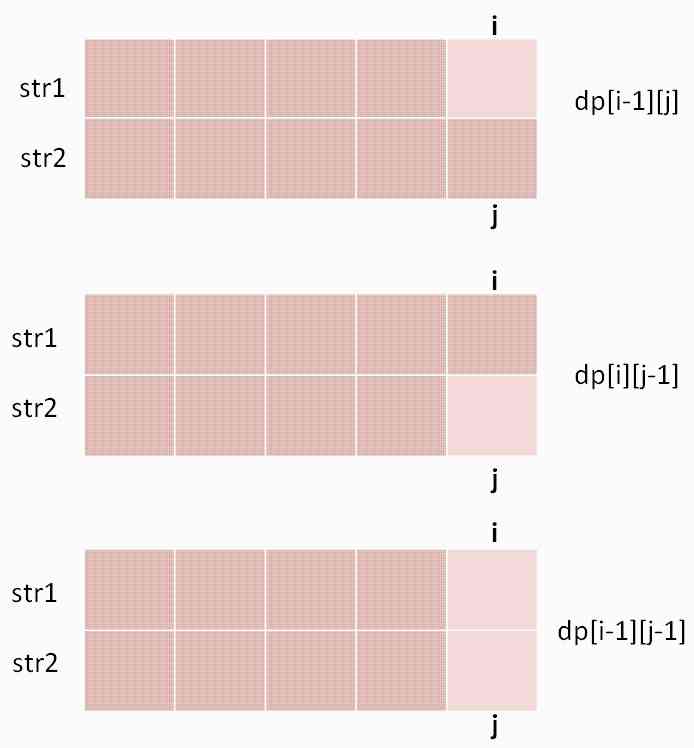
Look at it like this , obviously dp[i-1][j-1] Corresponding lcs The length cannot be larger than the first two cases , So there's no need to participate in the comparison .
3、 ... and 、 summary
For the dynamic programming of two strings , Generally speaking, it is defined as in this article DP table, Because there's a benefit to this definition , It's easy to write state transition equations ,dp[i][j] The state of can be derived from the previous state :
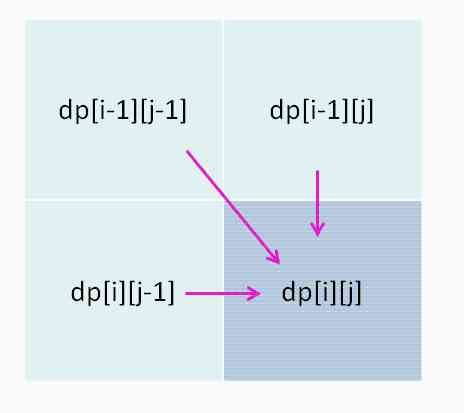
The way to find the state transition equation is , Think about what each state has 「 choice 」, As long as we can make the right choice with the right logic , The algorithm works correctly .
_____________
my Online e-books Yes 100 Original articles , Hands with brushes 200 Daoli is the subject , Recommended collection ! Corresponding GitHub Algorithm Repository We've got it 70k star, Welcome to mark star !