当前位置:网站首页>Prove the time complexity of heap sorting
Prove the time complexity of heap sorting
2022-07-06 12:43:00 【Lemon leaf C】
Time complexity of reactor building
Because the heap is a complete binary tree , A full binary tree is also a complete binary tree . To simplify , Full binary tree will be used to prove .( Time complexity is an approximation , So more nodes will not affect the final result ):
Suppose the height of the tree is  :
:
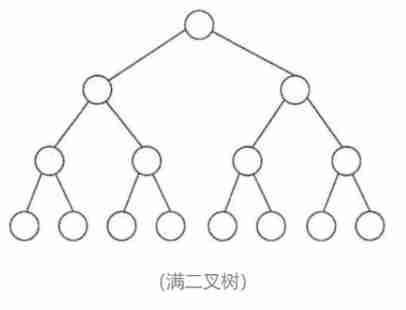
The first
layer :
Nodes , Need to move down
layer
The first
layer :
Nodes , Need to move down
layer
The first
layer :
Nodes , Need to move down
layer
The first
layer :
Nodes , Need to move down
layer
……
The first
layer :
Nodes , Need to move down
layer
The total number of moving steps of the mobile node is :
 ①
①
 ②
②
② - ① Dislocation subtraction :





therefore , The time complexity of reactor construction is 
边栏推荐
猜你喜欢
程序设计大作业:教务管理系统(C语言)
There is no red exclamation mark after SVN update
JS 函数提升和var变量的声明提升
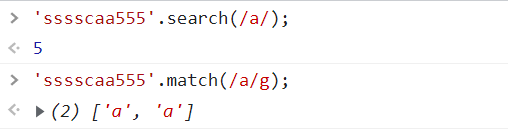
JS regular expression basic knowledge learning
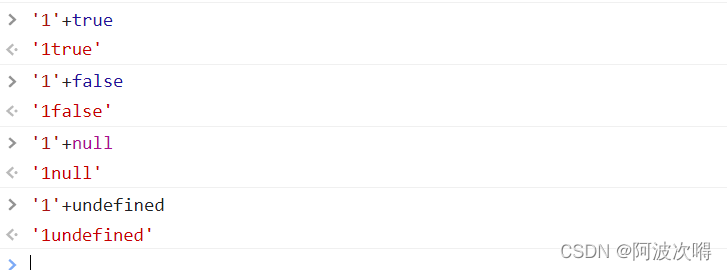
Types de variables JS et transformations de type communes

Pytorch: tensor operation (I) contiguous
![[Clickhouse kernel principle graphic explanation] about the collaborative work of partitioning, indexing, marking and compressed data](/img/28/221b0a51ef5f2e8ed5aeca2de8f463.jpg)
[Clickhouse kernel principle graphic explanation] about the collaborative work of partitioning, indexing, marking and compressed data
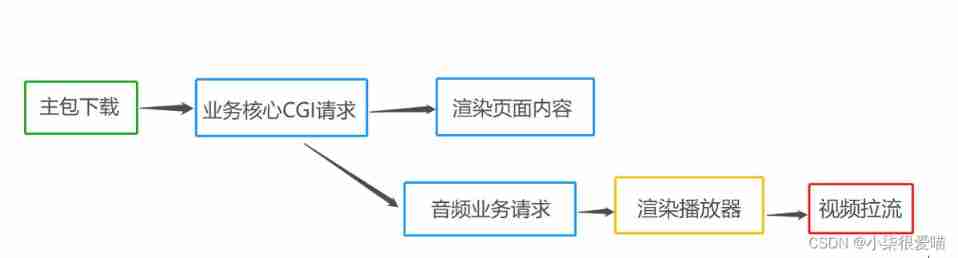
Page performance optimization of video scene
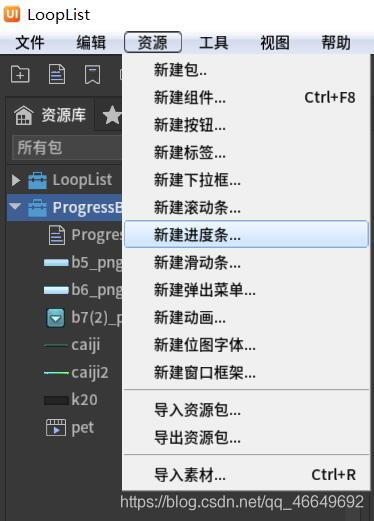
FairyGUI复选框与进度条的组合使用
编译原理:源程序的预处理及词法分析程序的设计与实现(含代码)
随机推荐
Office提示您的许可证不是正版弹框解决
(四)R语言的数据可视化——矩阵图、柱状图、饼图、散点图与线性回归、带状图
SVN更新后不出现红色感叹号
1041 be unique (20 points (s)) (hash: find the first number that occurs once)
Unity3d makes the registration login interface and realizes the scene jump
基于Redis的分布式锁 以及 超详细的改进思路
Postman 中级使用教程【环境变量、测试脚本、断言、接口文档等】
(五)R语言入门生物信息学——ORF和序列分析
FairyGUI人物状态弹窗
Learning notes of JS variable scope and function
1081 rational sum (20 points) points add up to total points
level16
关于Gateway中使用@Controller的问题
JS function promotion and declaration promotion of VaR variable
Redis based distributed ID generator
Teach you to release a DeNO module hand in hand
2022.2.12 resumption
MySQL時間、時區、自動填充0的問題
Design and implementation of general interface open platform - (39) simple and crude implementation of API services
[offer78]合并多个有序链表
 layer :
layer : Nodes , Need to move down
Nodes , Need to move down  layer
layer  layer :
layer : Nodes , Need to move down
Nodes , Need to move down  layer
layer  layer :
layer : Nodes , Need to move down
Nodes , Need to move down  layer
layer  layer :
layer : Nodes , Need to move down
Nodes , Need to move down  layer
layer  Nodes , Need to move down
Nodes , Need to move down