当前位置:网站首页>Use matlab to realize: chord cut method, dichotomy, CG method, find zero point and solve equation
Use matlab to realize: chord cut method, dichotomy, CG method, find zero point and solve equation
2022-07-02 07:23:00 【Drizzle】
Use Matlab Realization : String cutting 、 Dichotomy 、CG Law , Find zero 、 solve equations
String cutting
Example
seek x e x − 1 = 0 xe^x - 1 = 0 xex−1=0 The root of the , Initial value x 0 = 0.5 , x 1 = 0.6 . x_0 = 0.5, x_1 = 0.6. x0=0.5,x1=0.6.
Realization
Its mathematical iteration formula is :
x k + 1 = x k − f ( x k ) f ( x k ) − f ( x k − 1 ) ⋅ ( x k − x k − 1 ) x_{k + 1} = x_k - \frac{f(x_k)} {f(x_k) - f(x_{k - 1})} \cdot (x_k - x_{k - 1}) xk+1=xk−f(xk)−f(xk−1)f(xk)⋅(xk−xk−1)
Use Matlab Realization :
f = inline('x * e^x - 1');
x = 0;
xx = 0.5;
xxx = 0.6;
i=0;
while abs(xx-xxx) >= 1e-5
x = xx;
xx = xxx;
xxx = xx - f(xx) / (f(xx) - f(x)) * (xx - x);
i = i + 1;
end
After iteration 4 Time , obtain x 5 = 0.56714 x_5 = 0.56714 x5=0.56714.
If you need to see more decimal places , have access to :
format long g
Dichotomy
Example
Find the equation by dichotomy 2 e − x − s i n x = 0 2e^{-x} - sinx = 0 2e−x−sinx=0 In the interval [ 0 , 1 ] [0, 1] [0,1] The inner root , requirement ∣ x k − x ∗ ∣ < 1 2 × 1 0 − 5 | x_k - x^* | < \frac12 \times 10^{-5} ∣xk−x∗∣<21×10−5 .
Realization
First, find the endpoint value , Derivation , Make sure the function on the left is [ 0 , 1 ] [0, 1] [0,1] Have solution , And it is a single root interval .
take c = 0 , d = 1 c = 0, d = 1 c=0,d=1 , take [ c , d ] [c, d] [c,d] Bisection , Set the bisection point as x 0 = 1 2 ( c + d ) x_0 = \frac12 (c + d) x0=21(c+d) , Calculation f ( x 0 ) f(x_0) f(x0) , If f ( x 0 ) f(x_0) f(x0) And f ( c ) f(c) f(c) Same number ,……
d n − c n = 1 2 n ( d − c ) d_n - c_n = \frac1{2^n} (d - c) dn−cn=2n1(d−c) , as long as n Large enough , If there is a root, the length of the interval will be small enough , When the length meets the accuracy requirements , take x n = 1 2 ( c n + d n ) x_n = \frac12 (c_n + d_n) xn=21(cn+dn) As an approximation of the root of the equation .
Use Matlab Realization :
f = inline('2 * e^(-x) - sin(x)');
c = 0;
d = 1;
x = 1/2 * (c + d);
i = 0;
while d - c >= 1e-5/2
x = 1/2 * (c + d);
i ++;
if f(x) > 0
c = x;
elseif f(x) < 0
d = x;
else
break;
end;
end;
after 18 Sub iteration , c = x 17 c = x_{17} c=x17 when , d − c < 1 2 × 1 0 − 5 d - c < \frac12 \times 10^{-5} d−c<21×10−5 , The solution of the original equation is : x ∗ = 1 2 ( c 18 + d 18 ) = 0.92103 x^* = \frac12 (c_{18} + d_{18}) = 0.92103 x∗=21(c18+d18)=0.92103 .
CG Law
Example
take x 0 = ( 0 , 0 ) T , use C G Law seek Explain : x_0 = (0, 0)^T, use CG To solve : x0=(0,0)T, use CG Law seek Explain :
[ 6 3 3 2 ] ⋅ [ x 1 x 2 ] = [ 0 − 1 ] \left[\begin{array}{cc} 6 & 3\\ 3 & 2\\ \end{array}\right] \cdot \left[\begin{array}{c} x_1\\ x_2\\ \end{array}\right] = \left[\begin{array}{c} 0\\ -1\\ \end{array}\right] [6332]⋅[x1x2]=[0−1]
Realization
The equations are reduced to : A ⋅ x = b A \cdot x = b A⋅x=b .
take x 0 = ( 0 , 0 ) T , r 0 = b − A x 0 = ( 0 , − 1 ) T , p 0 = r 0 x_0 = (0, 0)^T,r_0 = b - Ax_0 = (0, -1)^T,p_0 = r_0 x0=(0,0)T,r0=b−Ax0=(0,−1)T,p0=r0
α 0 = ( r 0 , r 0 ) ( p 0 , A p 0 ) = 1 2 \alpha_0 = \frac{(r_0, r_0)}{(p_0, Ap_0)} = \frac12 α0=(p0,Ap0)(r0,r0)=21
x 1 = x 0 + α 0 ⋅ p 0 = ( 0 , − 1 2 ) T x_1 = x_0 + \alpha_0 \cdot p_0 = (0, -\frac12)^T x1=x0+α0⋅p0=(0,−21)T
r 1 = r 0 − α 0 ⋅ A ⋅ p 0 = ( 3 2 , 0 ) T r_1 = r_0 - \alpha_0 \cdot A \cdot p_0 = (\frac32, 0)^T r1=r0−α0⋅A⋅p0=(23,0)T
β 0 = ( r 1 , r 1 ) ( r 0 , r 0 ) = 9 4 \beta_0 = \frac{(r_1, r_1)}{(r_0, r_0)} = \frac94 β0=(r0,r0)(r1,r1)=49
p 1 = r 1 + β ⋅ p 0 = ( 3 2 , − 9 4 ) T p_1 = r_1 + \beta \cdot p_0 = (\frac32, -\frac94)^T p1=r1+β⋅p0=(23,−49)T
α 1 = ( r 1 , r 1 ) ( p 1 , A p 1 ) = 2 3 \alpha_1 = \frac{(r_1, r_1)}{(p_1, Ap_1)} = \frac23 α1=(p1,Ap1)(r1,r1)=32
x 2 = x 1 + α 1 ⋅ p 1 = ( 1 , − 2 ) T x_2 = x_1 + \alpha_1 \cdot p_1 = (1, -2)^T x2=x1+α1⋅p1=(1,−2)T
r 2 = r 1 − α 1 ⋅ A ⋅ p 1 = ( 0 , 0 ) T r_2 = r_1 - \alpha_1 \cdot A \cdot p_1 = (0, 0)^T r2=r1−α1⋅A⋅p1=(0,0)T
stay r k = 0 or ( p k , A p k ) = 0 r_k = 0 or (p_k, Ap_k) = 0 rk=0 or (pk,Apk)=0 when , Calculation termination , Yes x k = x ∗ x_k = x^* xk=x∗ .
Use Matlab Realization :
x = [0;0];
A = [6,3;3,2];
b = [0;-1];
r = b - A * x;
p = r;
i = 0;
while !all(r == [0;0]) && !all(dot(p, A * p) == [0;0])
alpha = dot(r, r) / dot(p, A * p);
xx = x + alpha * p;
rr = r - alpha * A * p;
beta = dot(rr, rr) / dot(r, r);
pp = rr + beta * p;
i ++;
r = rr;
x = xx;
p = pp;
end;
边栏推荐
- Oracle RMAN semi automatic recovery script restore phase
- CSRF攻击
- Explanation of suffix of Oracle EBS standard table
- MySQL组合索引加不加ID
- ORACLE EBS 和 APEX 集成登录及原理分析
- DNS attack details
- 一个中年程序员学习中国近代史的小结
- How to call WebService in PHP development environment?
- Sqli-labs customs clearance (less1)
- Illustration of etcd access in kubernetes
猜你喜欢

Message queue fnd in Oracle EBS_ msg_ pub、fnd_ Application of message in pl/sql

Changes in foreign currency bookkeeping and revaluation general ledger balance table (Part 2)
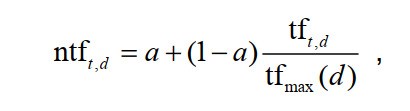
【信息检索导论】第六章 词项权重及向量空间模型

腾讯机试题

IDEA2020中测试PySpark的运行出错

The boss said: whoever wants to use double to define the amount of goods, just pack up and go
中年人的认知科普

一份Slide两张表格带你快速了解目标检测
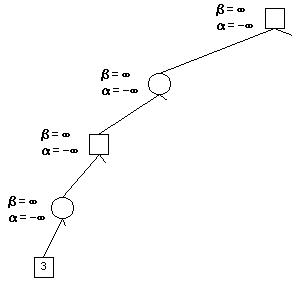
Alpha Beta Pruning in Adversarial Search

@Transitional step pit
随机推荐
view的绘制机制(一)
ERNIE1.0 与 ERNIE2.0 论文解读
Pyspark build temporary report error
Transform the tree structure into array in PHP (flatten the tree structure and keep the sorting of upper and lower levels)
Network security -- intrusion detection of emergency response
CRP实施方法论
实现接口 Interface Iterable&lt;T&gt;
Sqli labs customs clearance summary-page1
Cognitive science popularization of middle-aged people
矩阵的Jordan分解实例
spark sql任务性能优化(基础)
Yolov5 practice: teach object detection by hand
Find in laravel8_ in_ Usage of set and upsert
view的绘制机制(三)
Ceaspectuss shipping company shipping artificial intelligence products, anytime, anywhere container inspection and reporting to achieve cloud yard, shipping company intelligent digital container contr
Principle analysis of spark
Practice and thinking of offline data warehouse and Bi development
华为机试题-20190417
[Bert, gpt+kg research] collection of papers on the integration of Pretrain model with knowledge
The first quickapp demo