当前位置:网站首页>Codeforces Round #771 (Div. 2)
Codeforces Round #771 (Div. 2)
2022-07-06 09:14:00 【%xiao Q】
A. Reverse
这题我们只需要把数组和按顺序排的数组(1,2,3…n)比较即可,找到第一个不相等的位置 l,然后继续在后面数组找到 l 位置原本应该放的最小的数字(即 l)的数的下标 r,然后翻转[l, r],如果都相等,那么这个就是最小的,直接输出
参考代码:
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <cmath>
#include <queue>
#include <algorithm>
#include <unordered_map>
#define LL long long
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define reps(i, a, b) for(int i = a; i < b; i++)
#define pre(i, a, b) for(int i = b; i >= a; i--)
using namespace std;
const int N = 510;
int a[N], b[N];
int main()
{
int T;
cin >> T;
while(T--)
{
int n;
cin >> n;
rep(i, 1, n) cin >> a[i], b[i] = i;
int l = -1, r;
rep(i, 1, n)
if(a[i] != b[i])
{
l = i;
break;
}
if(l == -1)
{
rep(i, 1, n) cout << a[i] << ' ';
cout << endl;
continue;
}
rep(i, 1, n)
if(a[i] == b[l])
{
r = i;
break;
}
rep(i, 1, l - 1) cout << a[i] << ' ';
pre(i, l, r) cout << a[i] << ' ';
rep(i, r + 1, n) cout << a[i] << ' ';
cout << endl;
}
return 0;
}
B. Odd Swap Sort
这题我们可以按照奇偶性来将这些数划分为2个数组,根据题目要求,只有a[i] + a[i + 1]为奇数才可以交换,所以想要交换2个相邻的数,那么他们的奇偶性快点不同,所以我们可以按顺序枚举,将这些数分为2个数组(奇数和偶数数组),然后判断这2个数组里面是否存在a[i] > a[i + 1],因为奇偶性相同是不能交换的,想要把大的数往后面交换,那么他们2个数肯定要交换一次,如果不存在,那么就可以排成有序,反之不能。
参考代码:
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <cmath>
#include <queue>
#include <algorithm>
#include <unordered_map>
#define LL long long
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define reps(i, a, b) for(int i = a; i < b; i++)
#define pre(i, a, b) for(int i = b; i >= a; i--)
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
int main()
{
int T;
cin >> T;
while(T--)
{
int n, n1 = 0, n2 = 0;
cin >> n;
rep(i, 1, n)
{
int x;
cin >> x;
if(x & 1) a[n1++] = x;
else b[n2++] = x;
}
bool flag = true;
rep(i, 0, n1 - 2)
if(a[i] > a[i + 1]) flag = false;
rep(i, 0, n2 - 2)
if(b[i] > b[i + 1]) flag = false;
if(flag) puts("Yes");
else puts("No");
}
return 0;
}
C. Inversion Graph
这题我们可以利用一个单调递增的栈来做,栈内每个元素代表一个连通块中最大的元素,
那么我们如何来维护这个栈呢?
首先安顺序遍历这个数组:
- a[i] > q.top():因为是单调栈,所以大于栈内所有的数,直接入栈为一个新的连通块
- a[i] < q.top() :这时一个判断q.top()是否可以和栈内其它元素连通,即栈内元素可以和a[i]相连(也就是q[i] > a[i]),这时我们只要把大于a[i]的数全部出栈即可,但是栈顶不能出栈。
参考代码:
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <algorithm>
#include <unordered_map>
#define LL long long
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define reps(i, a, b) for(int i = a; i < b; i++)
#define pre(i, a, b) for(int i = b; i >= a; i--)
using namespace std;
int main()
{
int T;
cin >> T;
while(T--)
{
stack<int> a;
int n;
cin >> n;
rep(i, 1, n)
{
int x;
cin >> x;
if(a.empty())
{
a.push(x);
continue;
}
if(x > a.top()) a.push(x);
else
{
int t = a.top();
while(!a.empty() && a.top() > x) a.pop();
a.push(t);
}
}
cout << a.size() << endl;
}
return 0;
}
边栏推荐
- Django running error: error loading mysqldb module solution
- 报错解决 —— io.UnsupportedOperation: can‘t do nonzero end-relative seeks
- Request object and response object analysis
- 项目实战-后台员工信息管理(增删改查登录与退出)
- Why can't I use the @test annotation after introducing JUnit
- AcWing 242. A simple integer problem (tree array + difference)
- Did you forget to register or load this tag 报错解决方法
- Swagger, Yapi interface management service_ SE
- Picture coloring project - deoldify
- Dotnet replaces asp Net core's underlying communication is the IPC Library of named pipes
猜你喜欢

Classes in C #
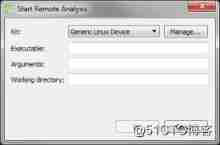
QT creator runs the Valgrind tool on external applications
Picture coloring project - deoldify
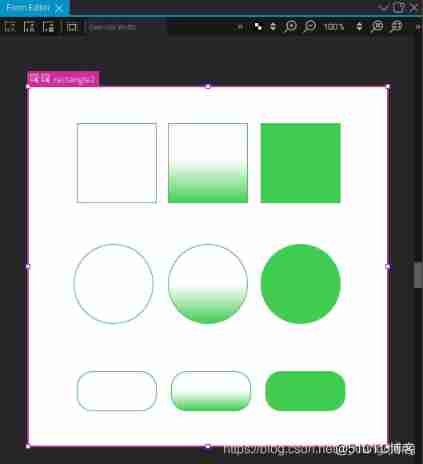
QT creator shape
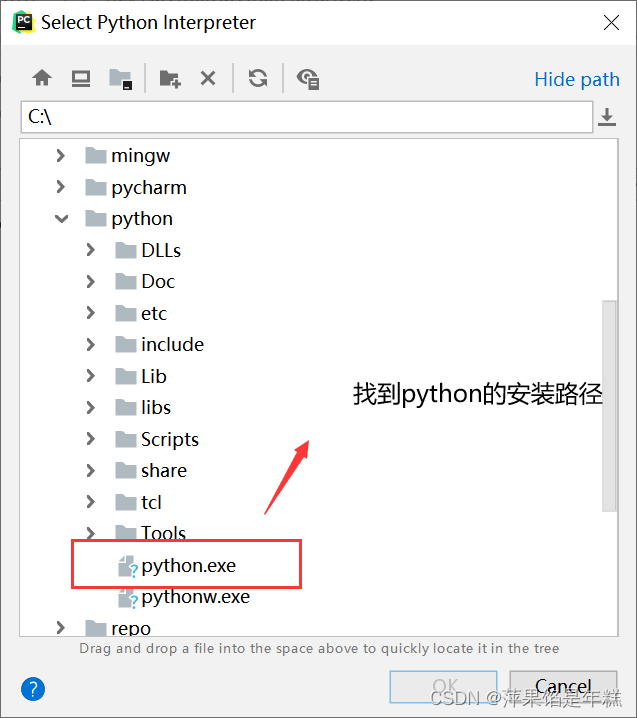
Unable to call numpy in pycharm, with an error modulenotfounderror: no module named 'numpy‘

图片上色项目 —— Deoldify
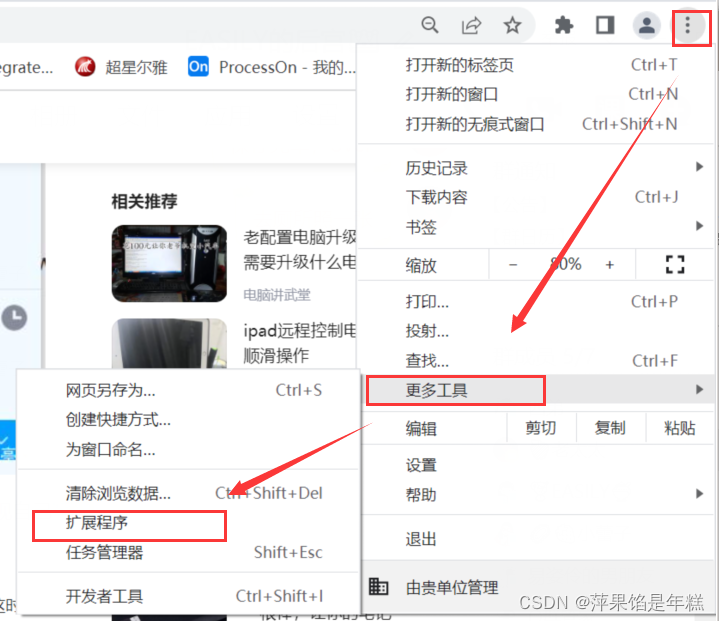
打开浏览器的同时会在主页外同时打开芒果TV,抖音等网站
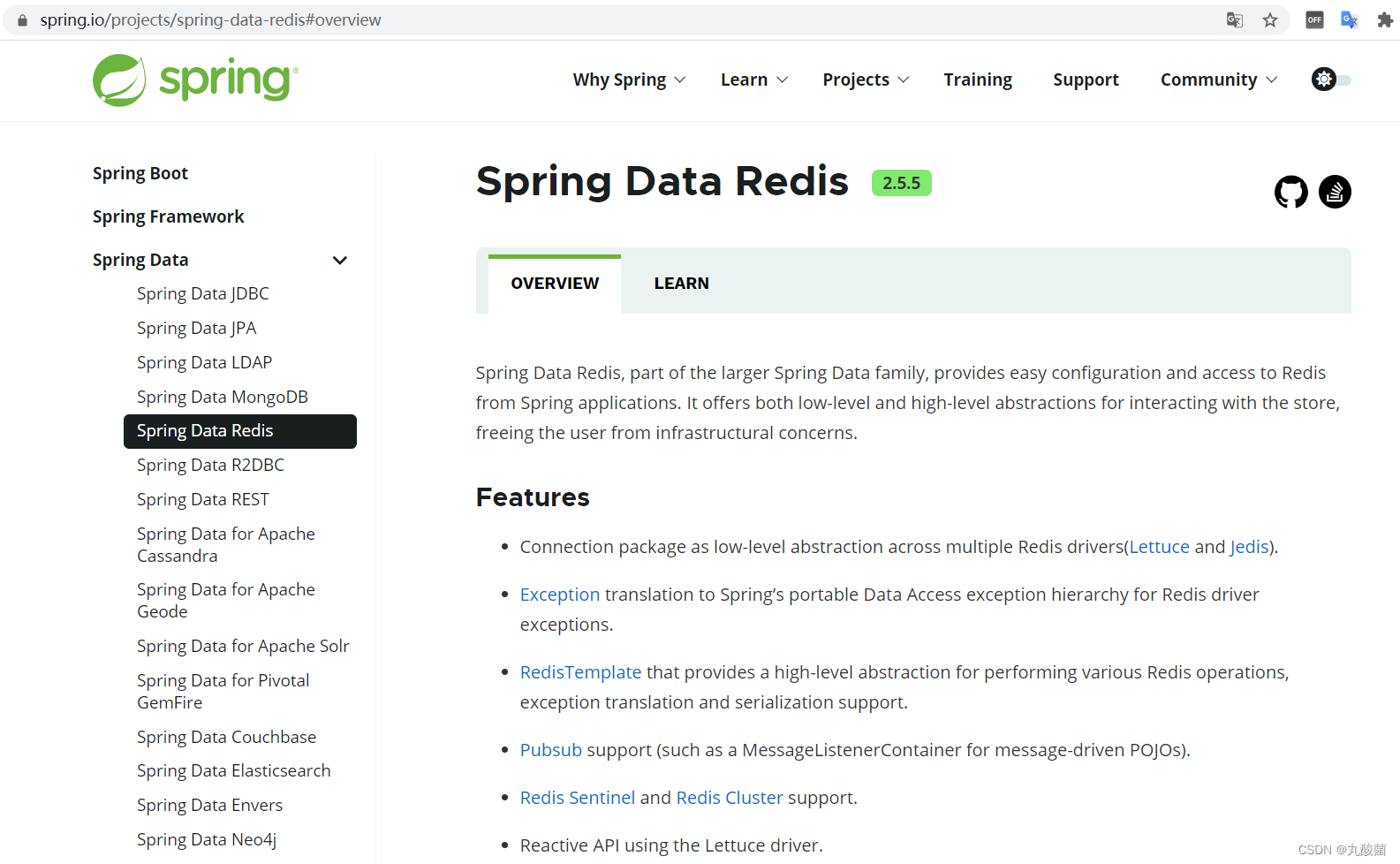
Basic use of redis
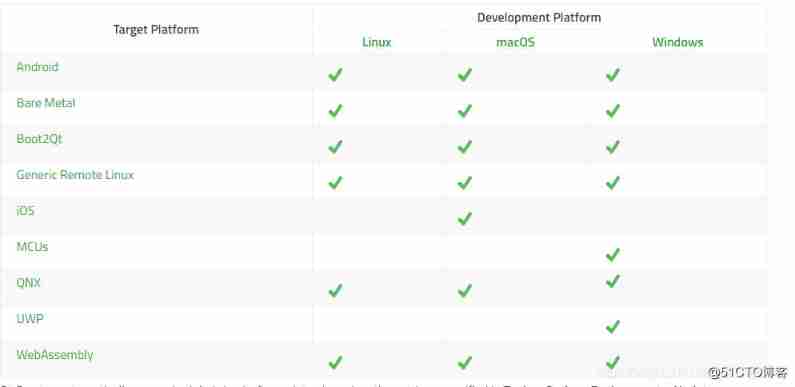
QT creator support platform
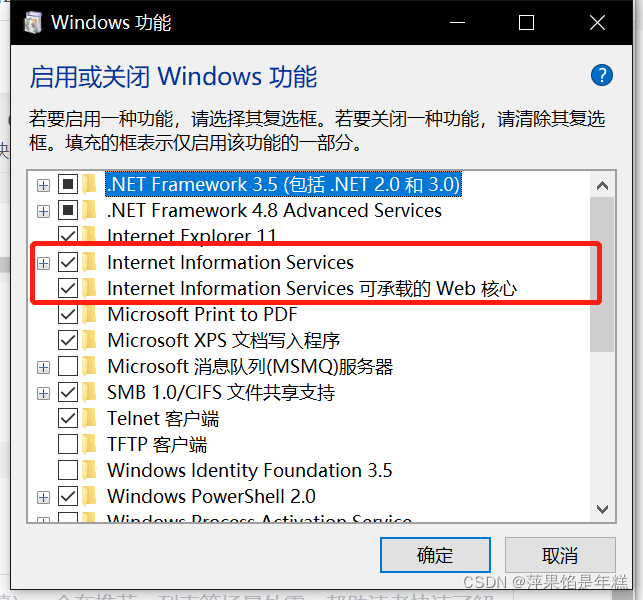
Learning question 1:127.0.0.1 refused our visit
随机推荐
Esp8266 at+cipstart= "", "", 8080 error closed ultimate solution
MySQL completely uninstalled (windows, MAC, Linux)
QT creator create button
Julia 1.6 1.7 common problem solving
解决安装Failed building wheel for pillow
windows下同时安装mysql5.5和mysql8.0
Asp access Shaoxing tourism graduation design website
Image recognition - pyteseract TesseractNotFoundError: tesseract is not installed or it‘s not in your path
There are three iPhone se 2022 models in the Eurasian Economic Commission database
Use dapr to shorten software development cycle and improve production efficiency
软件测试与质量学习笔记3--白盒测试
Generate PDM file from Navicat export table
Invalid default value for 'create appears when importing SQL_ Time 'error reporting solution
[free setup] asp Net online course selection system design and Implementation (source code +lunwen)
Ubuntu 20.04 安装 MySQL
QT creator test
Introduction to the easy copy module
Tcp/ip protocol (UDP)
基于apache-jena的知识问答
How to set up voice recognition on the computer with shortcut keys