当前位置:网站首页>AcWing 1294. Cherry Blossom explanation
AcWing 1294. Cherry Blossom explanation
2022-07-06 11:16:00 【Octopus loving monster】
AcWing 1294. Cherry blossoms Answer key
Title Description
Given an integer n n n , Find how many positive integer pairs ( x , y ) (x,y) (x,y) Satisfy 1 x + 1 y = 1 n ! \dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{n!} x1+y1=n!1
Input format :
An integer n n n
Output format :
An integer , Indicates the number of pairs that meet the conditions
The answer is right 1 0 9 + 7 10^9+7 109+7 modulus
Data range
1 ≤ n ≤ 1 0 6 1\le n \le 10^6 1≤n≤106
Answer key
Look at the formula , Easy to launch x > n ! x > n! x>n! y > n ! y >n! y>n!
Two unknowns x , y x,y x,y, Knowing one of them, you can launch another
So we might as well set y = n ! + k y=n!+k y=n!+k
The transformed formula is
1 x + 1 n ! + k = 1 n ! \dfrac{1}{x}+\dfrac{1}{n!+k}=\dfrac{1}{n!} x1+n!+k1=n!1
Divide the formula on both sides to get n ! ( n ! + k ) + ( n ! ) x = x ( n ! + k ) n!(n!+k)+(n!)x=x(n!+k) n!(n!+k)+(n!)x=x(n!+k)
Change can get
x = n ! ( n ! + k ) k = ( n ! ) 2 k + n ! x=\dfrac{n!(n!+k)}{k}=\dfrac{(n!)^2}{k}+n! x=kn!(n!+k)=k(n!)2+n!
because x To satisfy the property of positive integers , So the problem turns into k The value of needs to become ( n ! ) 2 (n!)^2 (n!)2 The divisor of
The problem became Find the divisor of a number
To find the divisor, you can use Basic theorem of arithmetic
The basic theorem of arithmetic is as follows
Any positive integer can be uniquely determined by its prime factor ( among p i p_i pi Is its qualitative factor )
x = p 1 α 1 ⋅ p 2 α 2 ⋅ p 3 α 3 … ⋅ p n α n x=p_1^{\alpha_1} · p_2^{\alpha_2}·p_3^{\alpha_3}\dots·p_n^{\alpha_n} x=p1α1⋅p2α2⋅p3α3…⋅pnαn
According to the full arrangement formula, the number of factors is
( α 1 + 1 ) ⋅ ( α 2 + 1 ) ⋅ ( α 2 + 1 ) ⋅ ( α 2 + 1 ) (\alpha_1+1)·(\alpha_2+1)·(\alpha_2+1)·(\alpha_2+1) (α1+1)⋅(α2+1)⋅(α2+1)⋅(α2+1)
The problem becomes a solution ( n ! ) 2 (n!)^2 (n!)2 The prime factor of and the order of each prime factor
We can ask for ( n ! ) (n!) (n!) And the order of each prime factor, then multiply the order 2 You can get there ( n ! ) 2 (n!)^2 (n!)2 Solution
How to find ( n ! ) (n!) (n!) For the quality factor and the order of the quality factor, please refer to my other blog
AcWing 197. Factorial decomposition Answer key
Get ( n ! ) (n!) (n!) Multiply the order of the prime factor by 2, Finally, by using the calculation formula of the number of factors, we can get k All values of
For each of these k Each value has a x The value corresponds to , Then all the final values are the number of positive integer pairs
Complete code
import java.io.*;
import java.util.*;
public class Main {
static int n;
static final int N=1000010;
static final long MOD=1000000007;
static int[] Primes =new int[N];
static boolean[] isPrime =new boolean[N];
static int cnt=0;
static long ans=1;
public static void init(int n)// Linear sieve
{
Arrays.fill(isPrime,true);
for(int i=2;i<=n;i++) {
if (isPrime[i])
Primes[cnt++] = i;
for(int j=0;j<cnt;j++)
{
int p=Primes[j];
if(i*p>n)
break;
isPrime[i*p]=false;
if(i%p==0)
{
break;
}
}
}
}
public static void main(String[] agrs) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
n=Integer.parseInt(reader.readLine());
init(n);
for(int i=0;i<cnt;i++)// Decomposing the prime factor
{
int tmp=n;
int p=Primes[i];
long res=0;
while(tmp>0)
{
res+=tmp/p;
tmp/=p;
}
res*=2;// The order of the prime factor converted to square
ans=(ans%MOD)*((res+1)%MOD);// Factor calculation formula
ans%=MOD;
}
System.out.println(ans);
}
}
边栏推荐
- Neo4j installation tutorial
- Software testing and quality learning notes 3 -- white box testing
- [free setup] asp Net online course selection system design and Implementation (source code +lunwen)
- Are you monitored by the company for sending resumes and logging in to job search websites? Deeply convinced that the product of "behavior awareness system ba" has not been retrieved on the official w
- Ansible practical Series III_ Task common commands
- Some problems in the development of unity3d upgraded 2020 VR
- Development of C language standard
- QT creator runs the Valgrind tool on external applications
- CSDN question and answer module Title Recommendation task (I) -- Construction of basic framework
- 项目实战-后台员工信息管理(增删改查登录与退出)
猜你喜欢
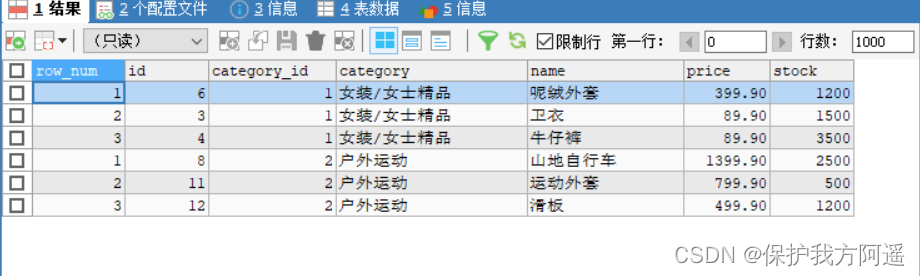
Other new features of mysql18-mysql8

QT creator create button

CSDN markdown editor
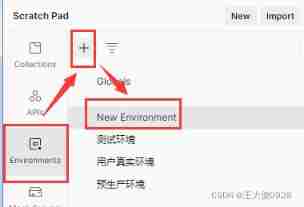
Postman environment variable settings
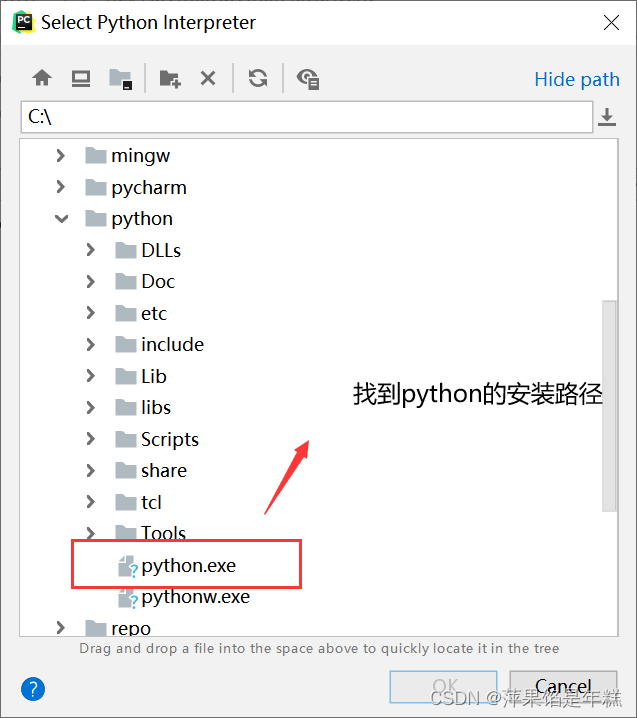
PyCharm中无法调用numpy,报错ModuleNotFoundError: No module named ‘numpy‘

csdn-Markdown编辑器
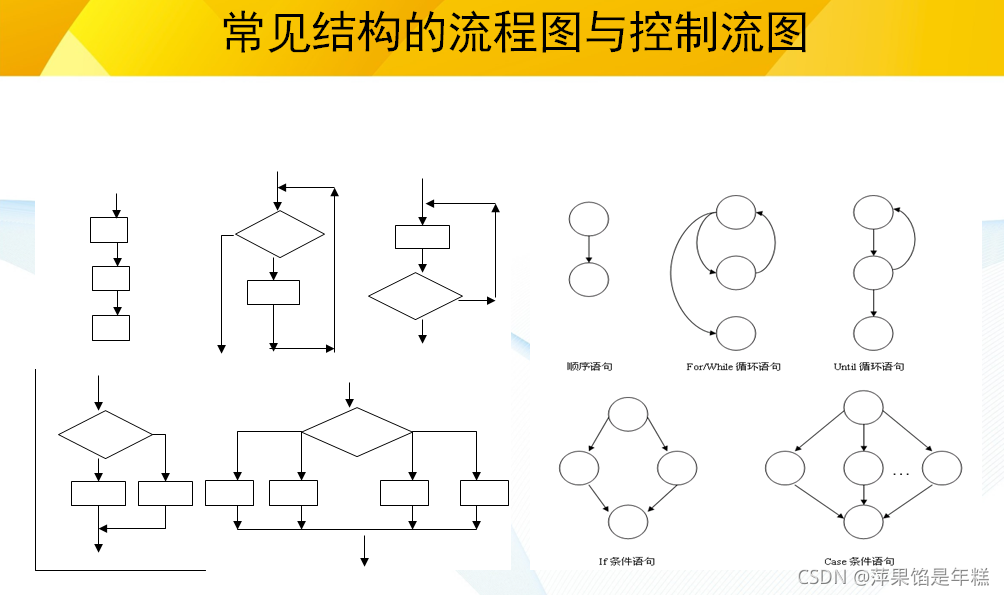
软件测试与质量学习笔记3--白盒测试

【博主推荐】SSM框架的后台管理系统(附源码)
Swagger、Yapi接口管理服务_SE
error C4996: ‘strcpy‘: This function or variable may be unsafe. Consider using strcpy_s instead
随机推荐
Django运行报错:Error loading MySQLdb module解决方法
Software testing and quality learning notes 3 -- white box testing
连接MySQL数据库出现错误:2059 - authentication plugin ‘caching_sha2_password‘的解决方法
虚拟机Ping通主机,主机Ping不通虚拟机
FRP intranet penetration
Database advanced learning notes -- SQL statement
SSM integrated notes easy to understand version
Deoldify project problem - omp:error 15:initializing libiomp5md dll,but found libiomp5md. dll already initialized.
[recommended by bloggers] C MVC list realizes the function of adding, deleting, modifying, checking, importing and exporting curves (with source code)
打开浏览器的同时会在主页外同时打开芒果TV,抖音等网站
Generate PDM file from Navicat export table
解决:log4j:WARN Please initialize the log4j system properly.
Asp access Shaoxing tourism graduation design website
【博主推荐】C#MVC列表实现增删改查导入导出曲线功能(附源码)
The virtual machine Ping is connected to the host, and the host Ping is not connected to the virtual machine
Software testing - interview question sharing
Windows cannot start the MySQL service (located on the local computer) error 1067 the process terminated unexpectedly
Development of C language standard
Data dictionary in C #
Dotnet replaces asp Net core's underlying communication is the IPC Library of named pipes