当前位置:网站首页>[Li Kou brushing questions] one dimensional dynamic planning record (53 change exchanges, 300 longest increasing subsequence, 53 largest subarray and)
[Li Kou brushing questions] one dimensional dynamic planning record (53 change exchanges, 300 longest increasing subsequence, 53 largest subarray and)
2022-07-06 21:20:00 【Li xiaoenzi】
Catalog
Two 、300. The longest increasing subsequence
3、 ... and 、53. Maximum subarray and
One 、322. Change for
subject
Give you an array of integers coins , Coins of different denominations ; And an integer amount , Represents the total amount .
Calculate and return the amount needed to make up the total amount The minimum number of coins . If no combination of coins can make up the total amount , return -1 . You can think of the number of coins of each kind as infinite .

Their thinking
First of all, make it clear that dp Definition of array : Enter a target amount n, Returns the minimum number of coins to round up the target amount .
【base case】:amount = 0, return 0;
【 state 】: The only target amount ;
【 choice 】: Each coin chosen , It's equivalent to reducing the target amount .
【 State transition equation 】:
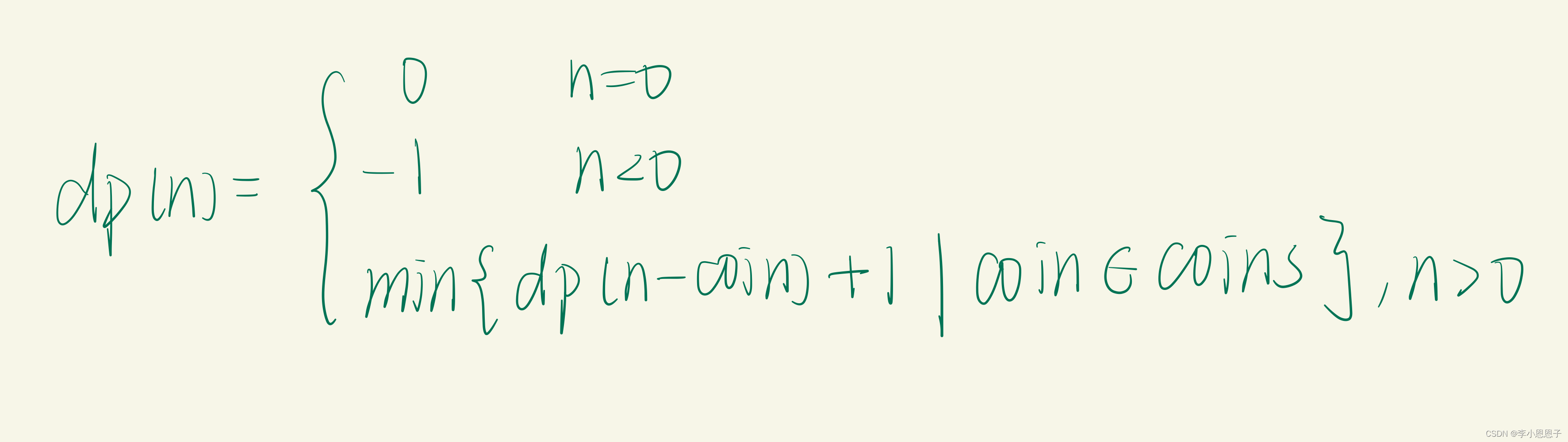
Code
The top-down : Search down with memory , Reduce the number of solving subproblems
class Solution {
public int coinChange(int[] coins, int amount) {
// A one-dimensional
// Memory search
//dp The array represents the input target amount amount Return the number of coins with the smallest target amount
int[] dp = new int[amount + 1];
for(int i = 0;i <= amount;i++){
dp[i] = -99;// Initialize a special value casually , Used to determine
}
return coin(coins,dp,amount);
}
public int coin(int[] coins,int[] dp,int amount){
if(amount == 0) return 0;
if(amount < 0) return -1;
// Don't double count , prune
if(dp[amount] != -99) return dp[amount];
int res = Integer.MAX_VALUE;
for(int coin = 0; coin < coins.length;coin++){
// Sub problem
int next = coin(coins,dp,amount-coins[coin]);
// There is no solution to the subproblem
if(next == -1) continue;
// Choose the optimal solution among all subproblems ,+1
res = Math.min(res,next + 1);
}
// Records of the results , Reduce double counting
dp[amount] = (res == Integer.MAX_VALUE) ? -1:res;
return dp[amount];
}
}Bottom up :dp Iterative solution of array
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
//amount+1 It's equivalent to infinity , Because the number of coins is the largest, that is amount( All for 1 The condition of a coin with pieces )
for(int i = 0;i < amount + 1 ; i++){
dp[i] = amount + 1;
}
dp[0] = 0;
for(int i = 0; i < amount + 1;i++){
// Find the optimal solution of all subproblems +1
for(int coin = 0; coin < coins.length; coin++){
if(i - coins[coin] < 0) continue;
dp[i] = Math.min(dp[i],dp[i - coins[coin]] + 1);
}
}
return (dp[amount] == amount + 1) ? -1 : dp[amount];
}
}Two 、300. The longest increasing subsequence
subject
Give you an array of integers nums , Find the length of the longest strictly increasing subsequence .
Subsequence Is a sequence derived from an array , Delete ( Or do not delete ) Elements in an array without changing the order of the rest . for example ,[3,6,2,7] It's an array [0,3,1,6,2,2,7] The subsequence .

Their thinking
Notice that you need to find subsequences , It's not a subarray , Subarray is continuous , Subsequence is not , You don't have to be continuous . As the example above 1 The subsequence 【2,3,7,101】.
dp Definition of array :dp[i] Said to nums[i] The longest increasing subsequence at the end of this number .
【base case】:dp[i] All values are initialized to 1, Because in order to nums[i] The longest increasing subsequence at the end at least includes itself
【 choice 】: For each of these dp[i], Just find all the smaller elements in front of it dp[j], Again +1, Find the maximum value, that is dp[i].
【 result 】: The maximum of subsequences , yes dp The maximum value in the array .
Code
class Solution {
public int lengthOfLIS(int[] nums) {
// Dynamic programming
// Definition dp[i] Represents the element nums[i] The longest increasing subsequence at the end
// For each of these dp[i], Just find all the smaller elements in front of it dp[j], Again +1, Find the maximum value, that is dp[i]
int[] dp = new int[nums.length];
for(int i = 0; i < nums.length;i++){
dp[i] = 1;// initialization , All elements are 1
}
int res = 1;
for(int i = 0; i < nums.length;i++){
for(int j = 0; j < i; j++){
if(nums[j] < nums[i]){
dp[i] = Math.max(dp[i],dp[j] + 1);
}
}
res = Math.max(res,dp[i]);
}
return res;
}
}3、 ... and 、53. Maximum subarray and
subject
Give you an array of integers nums , Please find a continuous subarray with the largest sum ( A subarray contains at least one element ), Return to its maximum and . Subarray Is a continuous part of the array .

Their thinking
And above 【 The longest increasing subsequence 】 similar , Definition dp Array meaning :dp[i] Said to nums[i] The largest subarray at the end and .
【 Be careful 】: If you define dp[i] The array is nums[0...i] The largest subarray in and , Then you can't find it , because Can't push it out dp[i+1], Subarray must be contiguous , But there is no guarantee dp[i] To dp[i+1] When :nums[0...i] The largest subarray in and nums[i+1] It's adjacent .
【base case】:dp[0] = nums[0]
【 choice 】: Judge the size and make a choice ,① Connect with the previous adjacent elements to form a larger sub array ;② Self as a subarray
【 result 】: The maximum sum of subarrays , yes dp The maximum value in the array .
Code
class Solution {
public int maxSubArray(int[] nums) {
// Dynamic programming
// Definition dp[i] Said to nums[i] The largest subarray at the end and
// There are two options for dynamic transfer , The first is combined with the previous element to form a larger sum , The second is to work in a group of your own
int[] dp = new int[nums.length];
dp[0] = nums[0];
for(int i = 1;i < nums.length;i++){
dp[i] = Math.max(nums[i],dp[i - 1] + nums[i]);
}
int res = Integer.MIN_VALUE;
for(int i = 0 ; i < nums.length;i++){
res = Math.max(res,dp[i]);
}
return res;
}
}In fact, the first thing I think about when I see this topic is sliding window , Because sliding window is most suitable for solving continuous substrings 、 Subarray and other problems , But there are negative numbers in this array element , You can't do it with a sliding window , because The conditions for changing the left and right pointers of the window are not clear .
Topic two 、 Topic 3 belongs to the same kind of dynamic programming problem .
边栏推荐
- Le langage r visualise les relations entre plus de deux variables de classification (catégories), crée des plots Mosaiques en utilisant la fonction Mosaic dans le paquet VCD, et visualise les relation
- 039. (2.8) thoughts in the ward
- 【滑动窗口】第九届蓝桥杯省赛B组:日志统计
- 每个程序员必须掌握的常用英语词汇(建议收藏)
- 防火墙基础之外网服务器区部署和双机热备
- ACdreamoj1110(多重背包)
- SAP Fiori应用索引大全工具和 SAP Fiori Tools 的使用介绍
- Manifest of SAP ui5 framework json
- for循环中break与continue的区别——break-完全结束循环 & continue-终止本次循环
- 快过年了,心也懒了
猜你喜欢
None of the strongest kings in the monitoring industry!
【深度学习】PyTorch 1.12发布,正式支持苹果M1芯片GPU加速,修复众多Bug

3D face reconstruction: from basic knowledge to recognition / reconstruction methods!
Introduction to the use of SAP Fiori application index tool and SAP Fiori tools
After working for 5 years, this experience is left when you reach P7. You have helped your friends get 10 offers
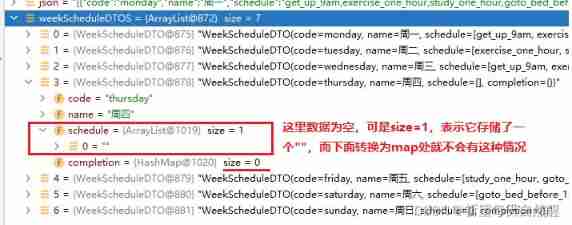
Fastjson parses JSON strings (deserialized to list, map)

爱可可AI前沿推介(7.6)
OneNote 深度评测:使用资源、插件、模版

967- letter combination of telephone number
The most comprehensive new database in the whole network, multidimensional table platform inventory note, flowus, airtable, seatable, Vig table Vika, flying Book Multidimensional table, heipayun, Zhix
随机推荐
KDD 2022 | realize unified conversational recommendation through knowledge enhanced prompt learning
Web开发小妙招:巧用ThreadLocal规避层层传值
SDL2来源分析7:演出(SDL_RenderPresent())
JS according to the Chinese Alphabet (province) or according to the English alphabet - Za sort &az sort
Reinforcement learning - learning notes 5 | alphago
在最长的距离二叉树结点
SAP UI5 框架的 manifest.json
JS traversal array and string
Replace Internet TV set-top box application through digital TV and broadband network
The difference between break and continue in the for loop -- break completely end the loop & continue terminate this loop
b站视频链接快速获取
Absolute primes (C language)
[sliding window] group B of the 9th Landbridge cup provincial tournament: log statistics
Start the embedded room: system startup with limited resources
Is this the feeling of being spoiled by bytes?
Four common ways and performance comparison of ArrayList de duplication (jmh performance analysis)
【Redis设计与实现】第一部分 :Redis数据结构和对象 总结
审稿人dis整个研究方向已经不仅仅是在审我的稿子了怎么办?
Opencv learning example code 3.2.3 image binarization
【mysql】触发器