当前位置:网站首页>leetcode:1139. 最大的以 1 为边界的正方形
leetcode:1139. 最大的以 1 为边界的正方形
2022-07-05 20:43:00 【OceanStar的学习笔记】
题目来源
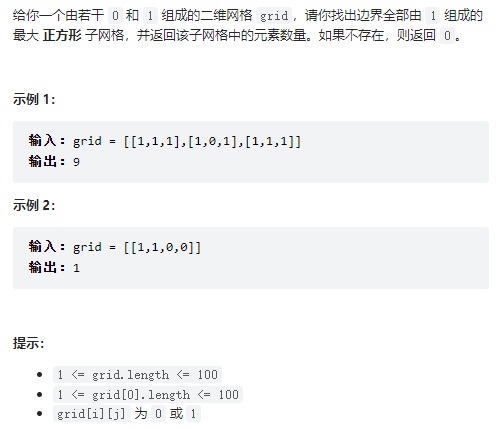
题目描述
class Solution {
public:
int largest1BorderedSquare(vector<vector<int>>& grid) {
}
};
举个例子:可以肉眼看出一个满足条件的数组边长为 33 ,同时也是最大边长。
vector<vector<int>> grid ={
{
0, 1, 0, 1, 1},
{
1, 1, 1, 1, 1},
{
1, 1, 0, 1, 1},
{
1, 1, 1, 1, 0},
{
0, 1, 1, 1, 1},
{
1, 1, 1, 0, 1},
{
0, 1, 1, 1, 1},
{
1, 1, 1, 0, 1}
};
std::vector<std::vector<int>> grid = {
{
1, 1, 1},
{
1, 0, 1},
{
1, 1, 1}
};
题目解析
动态规划
class Solution {
public:
// 运用动态规划的思想,建立一个三维数组来存储每个点的左侧和上方连续的1的个数
int largest1BorderedSquare(vector<vector<int>>& grid) {
if(grid.empty()){
return 0;
}
int length = grid.size(); //矩阵的长
int width = grid[0].size(); //矩阵的宽
//用dp[i][j][0]来表示第i行第j列的 左边 连续的1的个数
//用dp[i][j][1]来表示第i行第j列的 上面 连续的1的个数
std::vector<std::vector<std::vector<int>>> dp(
length + 1, std::vector<std::vector<int>>(
width + 1, std::vector<int>(
2, 0
)
)
);
int maxLen = 0;
for (int i = 1; i <= length; ++i) {
for (int j = 1; j <= width; ++j) {
if(grid[i - 1][j - 1] == 1){
//因为上面的代码 i 和 j 都是从1开始,到m,n结束,可以理解为在矩形的左边和上边加了一层0,所以实际的dp[i][j][0]其实是grid[i-1][j-1]左边连续的1的个数(包括自身),这样做其实就是为了方便初始化,避免写太多的if-else,是一种很常见的技巧
dp[i][j][0] += dp[i][j - 1][0] + 1;
dp[i][j][1] += dp[i - 1][j][1] + 1;
//尝试以第i行第j列(当前点)为右下角构成正方形
int len = std::min(dp[i][j][0], dp[i][j][1]); //最大可能长度
while (len > 0){
//判断这个可能的正方形右上角左侧是否有连续len个1 && 左下角的上方是否有连续len个1
if(dp[i - len + 1][j][0] >= len && dp[i][j - len + 1][1] >= len){
break;
}
len--;
}
maxLen = std::max(maxLen, len);
}
}
}
return maxLen * maxLen;
}
};
边栏推荐
- Mongodb basic exercises
- [record of question brushing] 1 Sum of two numbers
- 教你自己训练的pytorch模型转caffe(二)
- Open source SPL eliminates tens of thousands of database intermediate tables
- Common view container class components
- 资源道具化
- 线程池的使用
- Mongodb/ document operation
- Duchefa细胞分裂素丨二氢玉米素 (DHZ)说明书
- Codeforces Round #804 (Div. 2) - A, B, C
猜你喜欢

培养机器人教育创造力的前沿科技
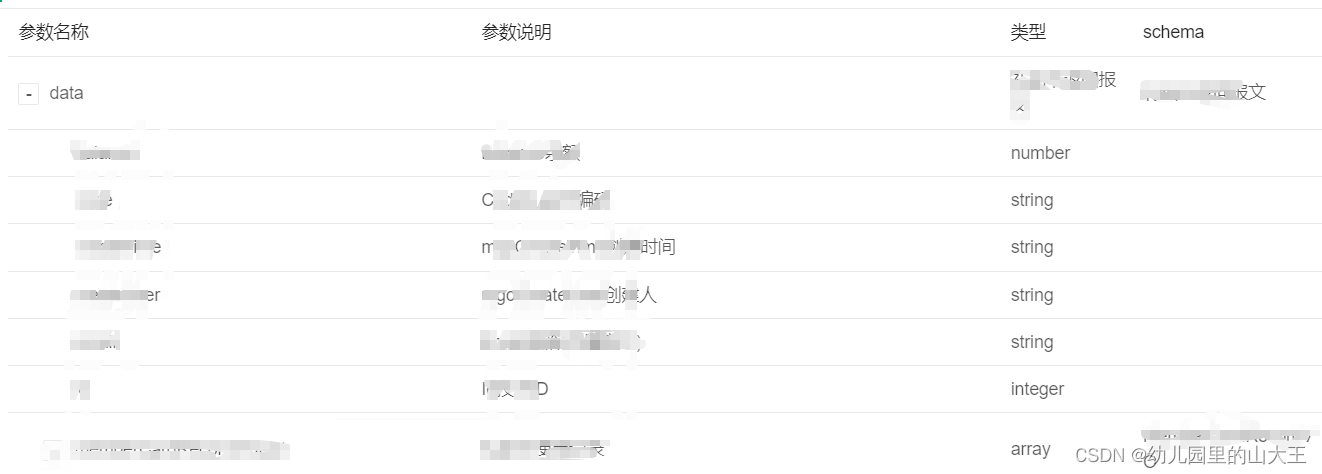
How to form standard interface documents

Applet page navigation
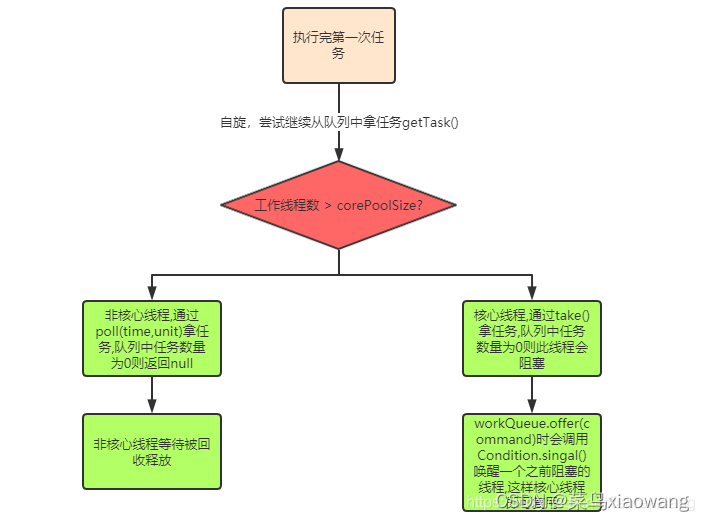
Use of thread pool

Duchefa p1001 plant agar Chinese and English instructions
![[quick start of Digital IC Verification] 2. Through an example of SOC project, understand the architecture of SOC and explore the design process of digital system](/img/1d/22bf47bfa30b9bdc2e8fd348180f49.png)
[quick start of Digital IC Verification] 2. Through an example of SOC project, understand the architecture of SOC and explore the design process of digital system
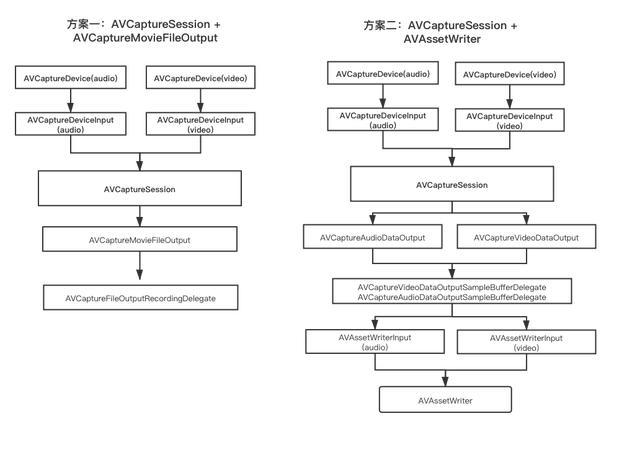
基于AVFoundation实现视频录制的两种方式
Use of form text box (II) input filtering (synthetic event)
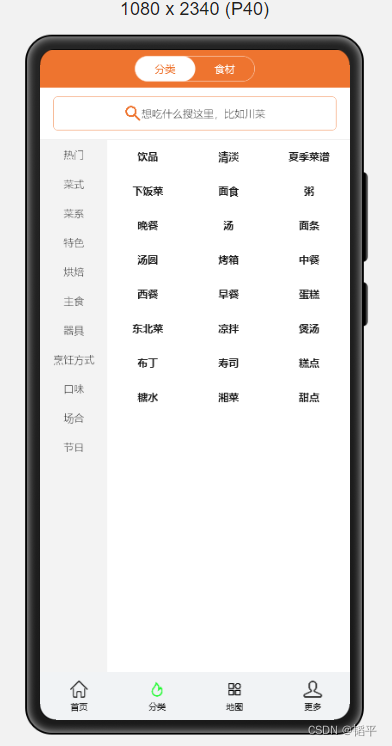
鸿蒙os第四次学习
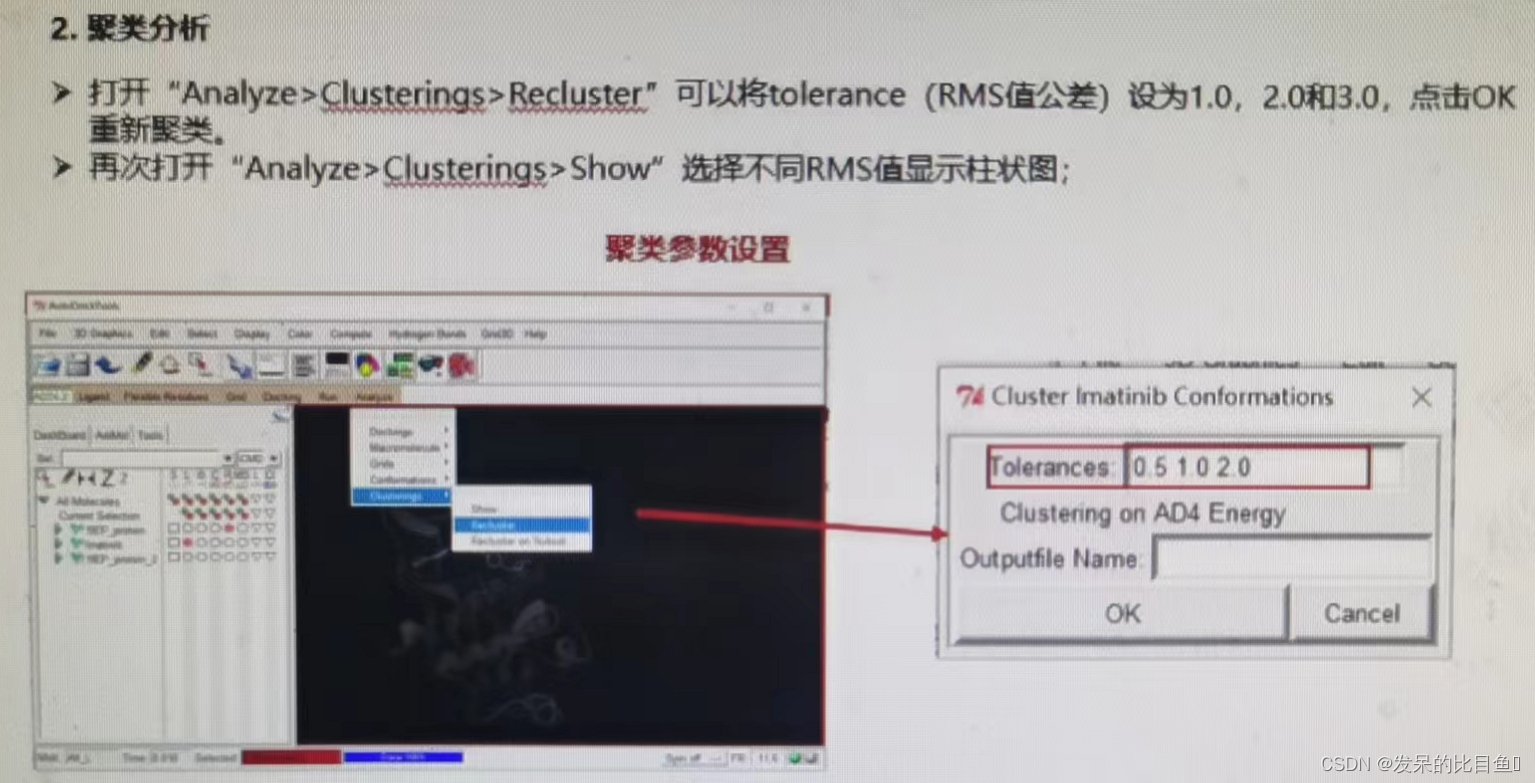
CADD course learning (7) -- Simulation of target and small molecule interaction (semi flexible docking autodock)
随机推荐
解析创客教育的知识迁移和分享精神
Duchefa丨D5124 MD5A 培养基中英文说明书
Chemical properties and application instructions of prosci Lag3 antibody
欢迎来战,赢取丰厚奖金:Code Golf 代码高尔夫挑战赛正式启动
Abnova丨培养细胞总 RNA 纯化试剂盒中英文说明书
Leetcode (347) - top k high frequency elements
手机开户股票开户安全吗?我家比较偏远,有更好的开户途径么?
Duchefa cytokinin dihydrozeatin (DHZ) instructions
重上吹麻滩——段芝堂创始人翟立冬游记
[UE4] unrealinsight obtains the real machine performance test report
2020 CCPC Weihai - A. golden spirit (thinking), D. ABC project (big number decomposition / thinking)
Implementation of redis unique ID generator
haas506 2.0开发教程 - 阿里云ota - pac 固件升级(仅支持2.2以上版本)
Classic implementation of the basic method of intelligent home of Internet of things
Informatics Olympiad 1337: [example 3-2] word search tree | Luogu p5755 [noi2000] word search tree
Is it safe to open a stock account by mobile phone? My home is relatively remote. Is there a better way to open an account?
Sort and projection
小程序代码的构成
IC popular science article: those things about Eco
线程池的使用