当前位置:网站首页>[Leetcode15]三数之和
[Leetcode15]三数之和
2022-07-06 09:17:00 【劲腰傩舞】
个人向,仅作记录回顾
双指针
问题
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
示例 2:
输入:nums = []
输出:[]
示例 3:
输入:nums = [0]
输出:[]
提示:
0 <= nums.length <= 3000
-105 <= nums[i] <= 105
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/3sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
vector<vector<int>> threeSum(vector<int>& nums) {
/* * 题目给了一个数组。要求枚举出所有三个数字相加等于零的组合。且组合不能重复。 * 直接用三重循环枚举的话。需要额外判断组合之间是否重复。 * 如果先对nums进行排序。要求枚举出来的三个数字有a<=b<=c。那么就可以避免重复。 */
sort(nums.begin(), nums.end());
/*获取nums大小。即将开始枚举。*/
int size = nums.size();
//存放结果
vector<vector<int>> ans;
for (int first = 0; first < size; first++) {
//在first=n-1的时候。开不出第二个for循环。
/*为了避免枚举出的组合的重复*/
if (first > 0 && nums[first] == nums[first - 1])
continue;
/*目标是三个数字的和等于零。那么随着second这个下标越来越大。third越来越小。 * 开始双指针。先初始化third */
int third = size - 1;
for (int second = first + 1; second < size; second++) {
/*还是为了避免枚举出的组合的重复*/
if (second > first + 1 && nums[second] == nums[second - 1])
continue;
/*还是先避免组合的重复*/
while (third > second && third < size - 1 && nums[third] == nums[third + 1])
third--;
/*不满足条件的话,继续左移third*/
while (third > second && nums[third] + nums[second] > -nums[first])
third--;
/*双指针重叠的时候。second指针继续右移的话。也不会再满足题意了 * 但是first还可以继续右移。 */
if (third == second)
break;
if (nums[third] + nums[second] == -nums[first])
/*初始化vector<int>的一种好用的方法{1,2,3}*/
ans.push_back({
nums[first],nums[second],nums[third] });
/*小于的情况不用考虑了。继续右移second就能解决*/
}
}
return ans;
}
边栏推荐
- 关于Gateway中使用@Controller的问题
- Detailed explanation of 5g working principle (explanation & illustration)
- Symbolic representation of functions in deep learning papers
- map文件粗略分析
- (三)R语言的生物信息学入门——Function, data.frame, 简单DNA读取与分析
- Dead loop in FreeRTOS task function
- ORA-02030: can only select from fixed tables/views
- ESP学习问题记录
- 程序员老鸟都会搞错的问题 C语言基础 指针和数组
- Whistle+switchyomega configure web proxy
猜你喜欢
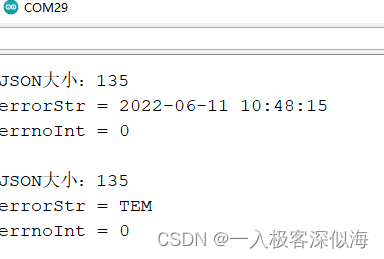
arduino JSON数据信息解析
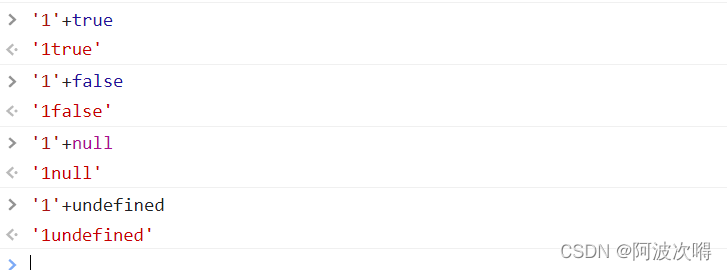
Types de variables JS et transformations de type communes
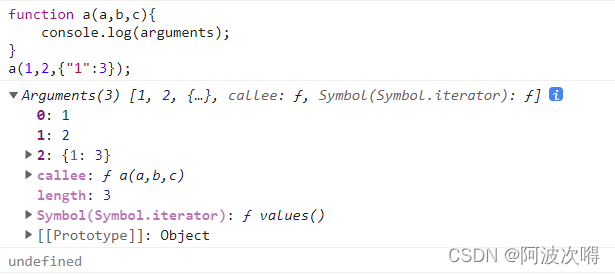
js 变量作用域和函数的学习笔记
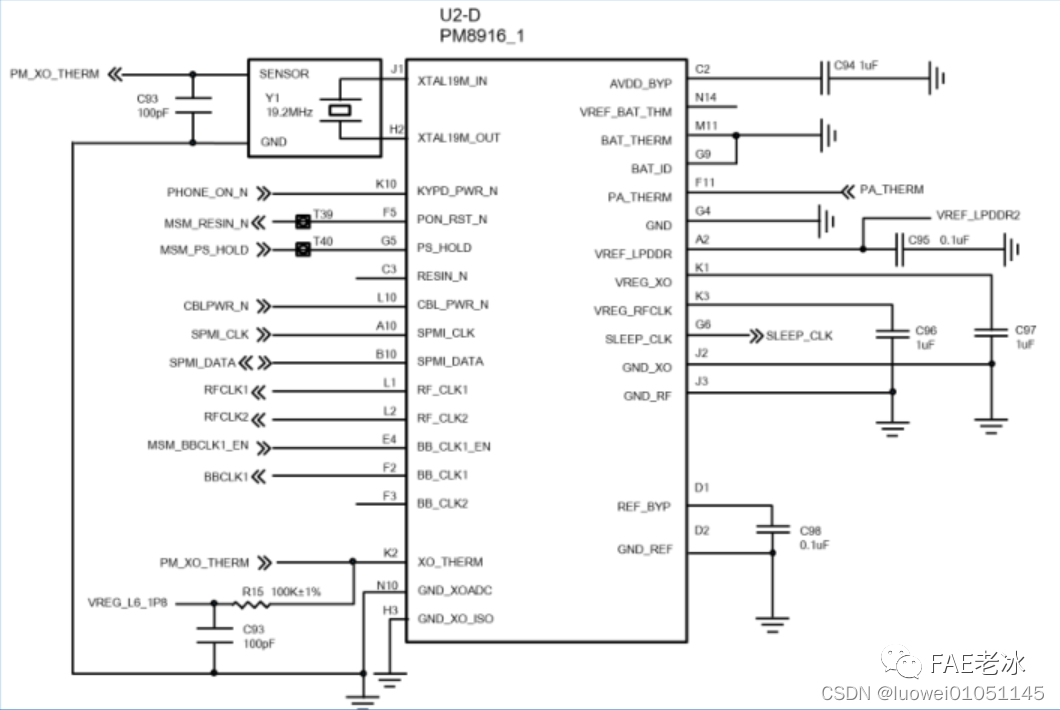
Working principle of genius telephone watch Z3
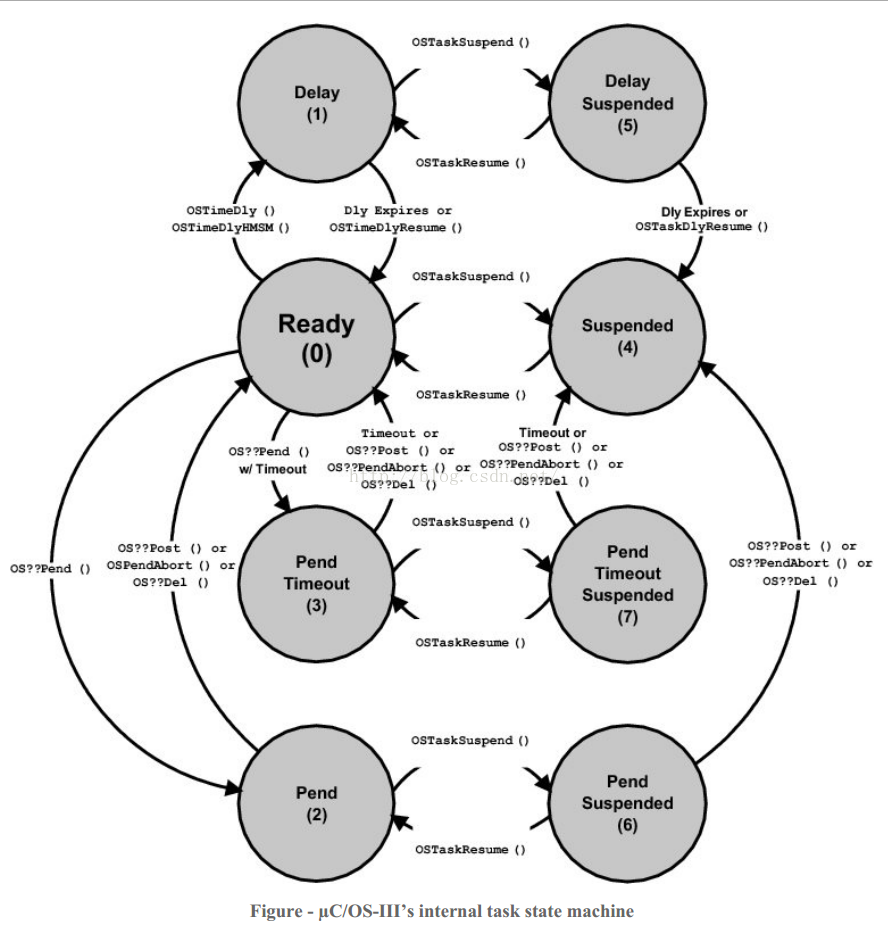
Characteristics, task status and startup of UCOS III

Stm32f1+bc20+mqtt+freertos system is connected to Alibaba cloud to transmit temperature and humidity and control LED lights

CUDA C programming authoritative guide Grossman Chapter 4 global memory

Basic operations of databases and tables ----- creating data tables
MySQL takes up too much memory solution
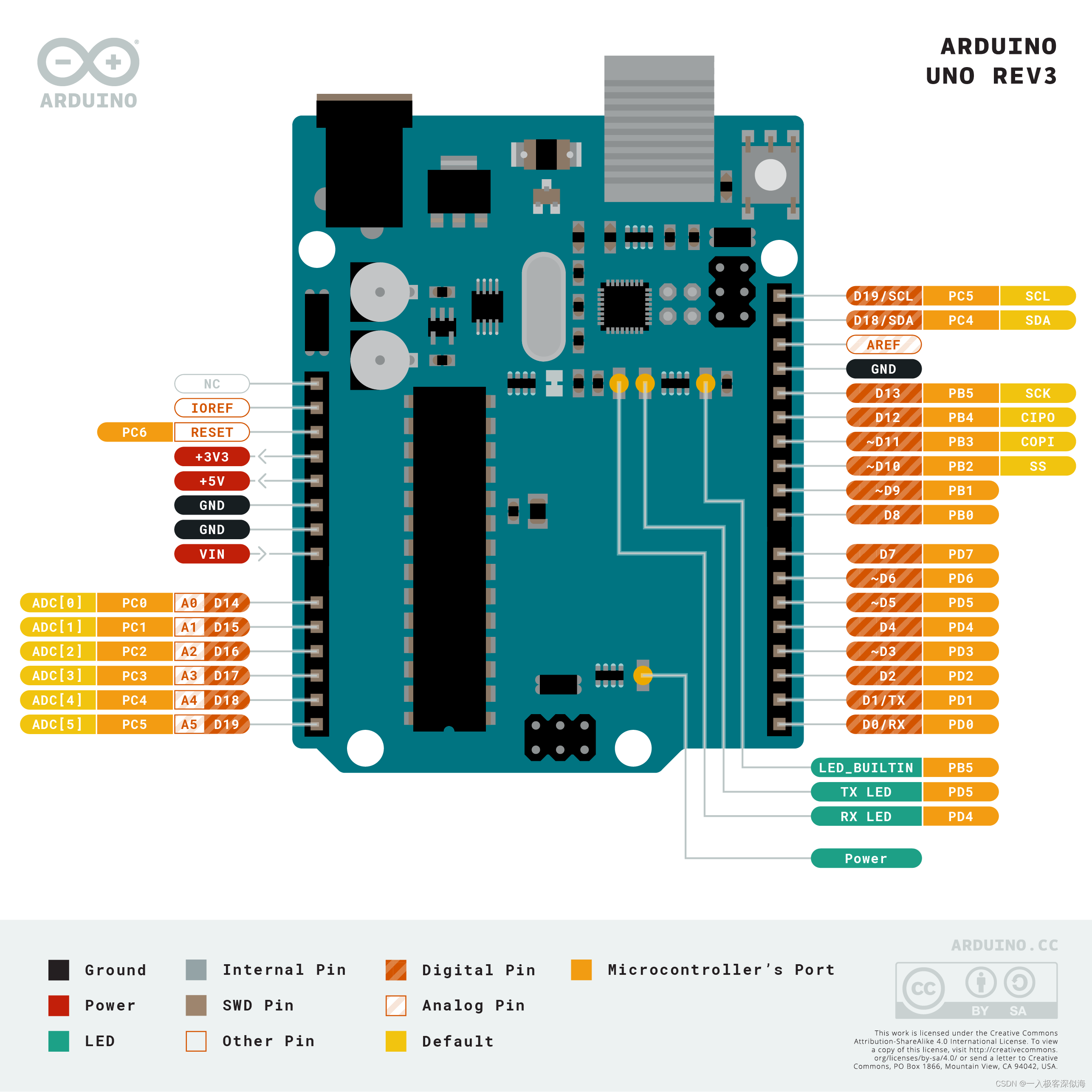
arduino UNO R3的寄存器写法(1)-----引脚电平状态变化
随机推荐
JS正则表达式基础知识学习
AMBA、AHB、APB、AXI的理解
Gravure sans fil Bluetooth sur micro - ordinateur à puce unique
Kconfig Kbuild
Common properties of location
map文件粗略分析
arduino获取随机数
如何给Arduino项目添加音乐播放功能
open-mmlab labelImg mmdetection
ES6 grammar summary -- Part I (basic)
RT thread API reference manual
C language callback function [C language]
Custom view puzzle getcolor r.color The color obtained by colorprimary is incorrect
Basic operations of databases and tables ----- creating data tables
Intermediate use tutorial of postman [environment variables, test scripts, assertions, interface documents, etc.]
ESP学习问题记录
The first simple case of GNN: Cora classification
imgcat使用心得
Arm pc=pc+8 is the most understandable explanation
GCC compilation options