当前位置:网站首页>Tensorflow2.0 自定义训练的方式求解函数系数
Tensorflow2.0 自定义训练的方式求解函数系数
2022-07-06 11:32:00 【赫凯】
做曲线拟合逼近的时候,如果知道拟合的大致方程,如何求出方程的系数呢?
其实在numpy中已经有函数去求多项式系数了,如下
# x和y对应的就是坐标轴上x和y。
z = np.polyfit(x, y, 3) #用3次多项式拟合,输出系数从高到0
# p就是所求方程
p = np.poly1d(z) #使用次数合成多项式
但是有时候曲线不只是多项式,而是指数函数、幂函数,这就需要我们自己写了,其实就和之前求线性函数的系数一样,只不过换了一个方程式
# 这里定义自变量和因变量x,y。
x = tf.constant([1, 2, 3, 4, 5, 6],dtype=tf.float64)
y = tf.constant([11, 23, 45, 46, 48, 59],dtype=tf.float64)
# 这里定义反传时需要更新的参数,也就是我们要求的参数
w_a = tf.Variable(-0.0, dtype=tf.float64,name='a')
w_b = tf.Variable(0.1, dtype=tf.float64,name='b')
w_c = tf.Variable(-0.0, dtype=tf.float64,name='c')
w_d = tf.Variable(2.1, dtype=tf.float64,name='d')
# 把我们的系数放在一个数组里,方便后面反传
variables=[w_a, w_b, w_c, w_d]
# 定义循环次数
epoch = 1000
# 定义优化器
optimizer=tf.keras.optimizers.Adam(learning_rate=1e-3)
# 循环
for e in range(epoch):
with tf.GradientTape() as tape:
# 预测函数
y_pred=w_a*tf.exp(w_b*x)+w_c*x+w_d
# 损失函数
loss=tf.reduce_sum(tf.square(y_pred-y))
# 对变量求导
grads=tape.gradient(loss, variables)
# 调整参数
optimizer.apply_gradients(grads_and_vars=zip(grads, variables))
# 打印结果
if e%100==0:
print(f"step: {
e}, loss: {
loss}, a: {
w_a.numpy()}, b: {
w_b.numpy()}, c: {
w_c.numpy()}, d: {
w_d.numpy()}")
# 输出参数
print(variables)
就酱
边栏推荐
- 今日直播 | “人玑协同 未来已来”2022弘玑生态伙伴大会蓄势待发
- 深入分析,Android面试真题解析火爆全网
- An error occurs when installing MySQL: could not create or access the registry key needed for the
- Word如何显示修改痕迹
- 【pytorch】yolov5 训练自己的数据集
- 学习探索-函数防抖
- 时钟轮在 RPC 中的应用
- R语言dplyr包进行数据分组聚合统计变换(Aggregating transforms)、计算dataframe数据的分组均值(mean)
- CCNP Part 11 BGP (III) (essence)
- Digital "new" operation and maintenance of energy industry
猜你喜欢
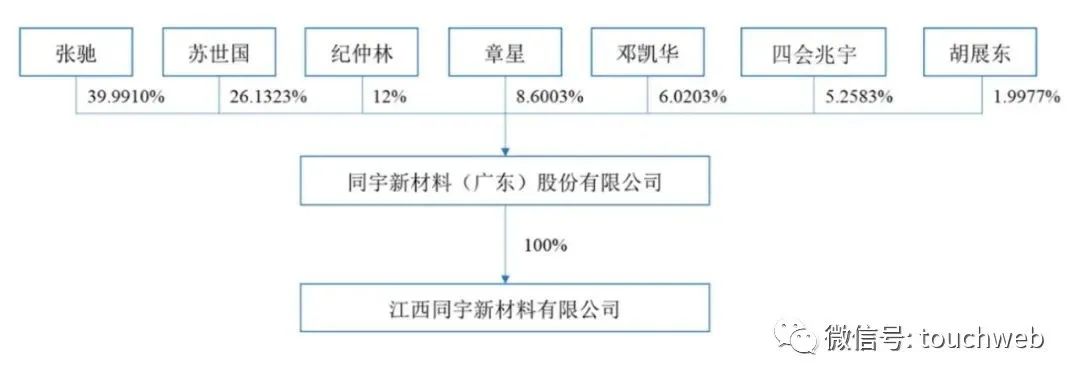
Tongyu Xincai rushes to Shenzhen Stock Exchange: the annual revenue is 947million Zhang Chi and Su Shiguo are the actual controllers

关于静态类型、动态类型、id、instancetype
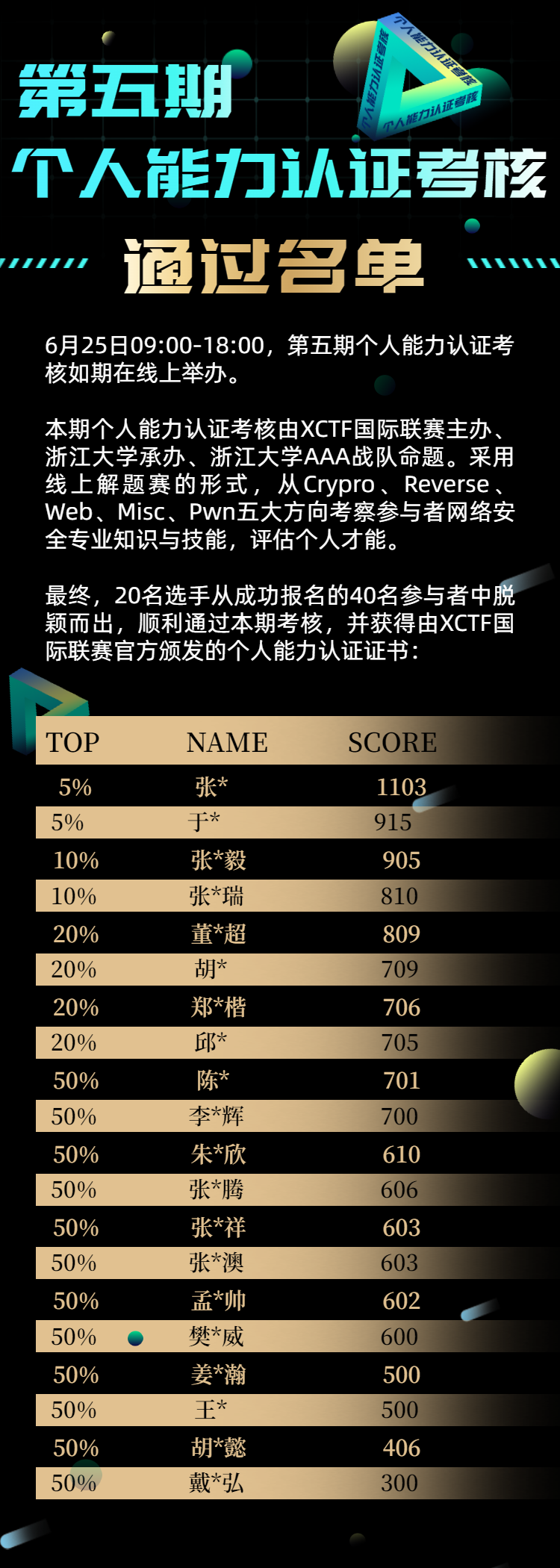
The list of people who passed the fifth phase of personal ability certification assessment was published

Help improve the professional quality of safety talents | the first stage of personal ability certification and assessment has been successfully completed!

How to improve website weight

黑馬--Redis篇

思维导图+源代码+笔记+项目,字节跳动+京东+360+网易面试题整理
![Airiot IOT platform enables the container industry to build [welding station information monitoring system]](/img/52/88e3c7b7a60867282921d9bb5c96da.jpg)
Airiot IOT platform enables the container industry to build [welding station information monitoring system]

学习探索-使用伪元素清除浮动元素造成的高度坍塌
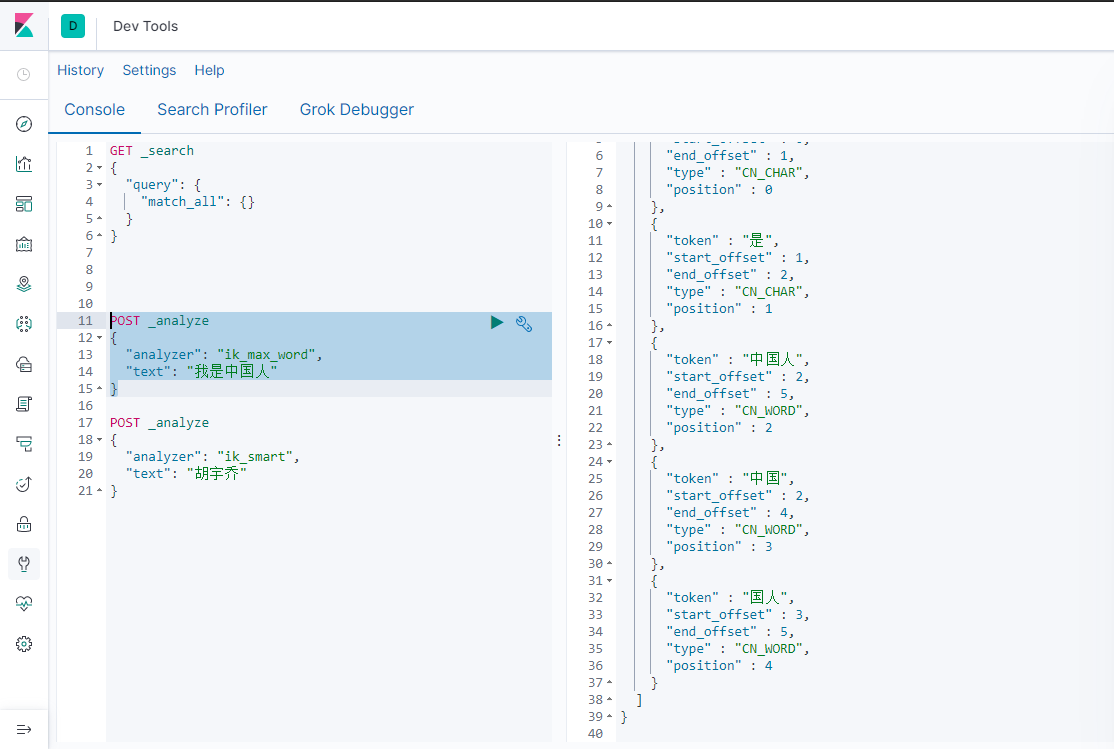
Cereals Mall - Distributed Advanced p129~p339 (end)
随机推荐
Cereals Mall - Distributed Advanced p129~p339 (end)
Countdown 2 days | live broadcast preview of Tencent cloud message queue data import platform
10 schemes to ensure interface data security
Mind map + source code + Notes + project, ByteDance + JD +360+ Netease interview question sorting
Graffiti intelligence is listed on the dual main board in Hong Kong: market value of 11.2 billion Hong Kong, with an annual revenue of 300 million US dollars
时钟轮在 RPC 中的应用
RT-Thread 组件 FinSH 使用时遇到的问题
R language uses DT function to generate t-distribution density function data and plot function to visualize t-distribution density function data
R language ggplot2 visual time series histogram: visual time series histogram through two-color gradient color matching color theme
Swagger2 reports an error illegal DefaultValue null for parameter type integer
GCC [7] - compilation checks the declaration of functions, and link checks the definition bugs of functions
Pytorch common loss function
Translation D28 (with AC code POJ 26:the nearest number)
Camel case with Hungarian notation
GCC【7】- 编译检查的是函数的声明,链接检查的是函数的定义bug
Help improve the professional quality of safety talents | the first stage of personal ability certification and assessment has been successfully completed!
Actf 2022 came to a successful conclusion, and 0ops team won the second consecutive championship!!
谷粒商城--分布式高级篇P129~P339(完结)
In 50W, what have I done right?
潇洒郎: AttributeError: partially initialized module ‘cv2‘ has no attribute ‘gapi_wip_gst_GStreamerPipe