当前位置:网站首页>Introduction to Chapter 8 proof problem of njupt "Xin'an numeral base"
Introduction to Chapter 8 proof problem of njupt "Xin'an numeral base"
2022-07-05 13:42:00 【huangx607087】
NJUPT 《 Confidence safe number base 》 Introduction to group theory proof problem
notes : This article is suitable for students who study the mathematical basis of information security to make a surprise attack before the exam , Not applicable to students majoring in Mathematics . Some of the contents may not be rigorous for the Department of Mathematics , But for students majoring in information security who want to cope with the exam, it is completely enough .
The fundamental reason why many students can't do modern algebra is that they don't understand the basic concepts , For the course of mathematics foundation of information security , It won't be as difficult as the mathematics department ( Engineering is mainly applied ), Therefore, the focus of review is to understand all the concepts . Instead of memorizing the topic .
This article It's all my own summary , Mainly Sort out the conceptual things 、 Sum up some How to solve the proof problem , Build a complete proof idea , Considering that there are few online resources , I'm bored during the winter vacation , Then write a message for the benefit of younger students and younger students .
First put a picture of Zhenlou . Then get to the point

1 Group
1.1 The concept of group
What is a group ? textbook P233 It's very messy . In short : A group is a group with ** Sealing property 、 Can be combined with 、 There is only one yuan 、 An algebraic system in which any element is reversible . ** So by definition , We can easily get the properties of groups :
The properties of groups : In groups < G , ∗ > <G,*> <G,∗> in , Yes :
1. Sealing property : namely ∀ a , b ∈ G \forall a,b \in G ∀a,b∈G , There are a b ∈ G ab\in G ab∈G.
2. associativity : namely ∀ a , b , c ∈ G \forall a,b,c \in G ∀a,b,c∈G, There are a ( b c ) = ( a b ) c a(bc)=(ab)c a(bc)=(ab)c establish
3. There is only one yuan : That is, there is an element in the Group e e e , bring ∀ a ∈ G \forall a \in G ∀a∈G , There are a e = e a = a ae=ea=a ae=ea=a establish .
4. Any element is reversible : namely ∀ a ∈ G \forall a \in G ∀a∈G , ∃ b ∈ G \exists b \in G ∃b∈G , bring a b = b a = e ab=ba=e ab=ba=e establish . here b b b be called a a a Inverse element , Write it down as a − 1 a^{-1} a−1
Operations in groups are not necessarily commutative , If it is exchangeable , So this group is a commutative group .
So if we want to prove an algebraic system < G , ∗ > <G,*> <G,∗> It's a group , Then we use the definition method to prove , It's like writing eight part essay .
Example 1: prove < Z , + > <\Z,+> <Z,+> It's a group . among Z \Z Z It's a set of integers , + + + It's ordinary addition .
①: because ∀ a , b ∈ Z \forall a,b \in \Z ∀a,b∈Z , There are a + b ∈ Z a+b \in \Z a+b∈Z Hang up . Therefore, the closeness of operation is established
②: because ∀ a , b , c ∈ Z \forall a,b,c \in \Z ∀a,b,c∈Z , There are ( a + b ) + c = a + ( b + c ) (a+b)+c=a+(b+c) (a+b)+c=a+(b+c) establish . Therefore, the operation is associative .
③: because ∀ a ∈ Z \forall a \in \Z ∀a∈Z , There are a + 0 = 0 + a = a a+0=0+a=a a+0=0+a=a , Therefore, the operation has a unitary 0 0 0 .
④: because ∀ a ∈ Z \forall a \in \Z ∀a∈Z , There are − a ∈ Z -a \in \Z −a∈Z , bring a + ( − a ) = ( − a ) + a = 0 a+(-a) =(-a)+a=0 a+(−a)=(−a)+a=0 establish . Therefore, any element in the set has an additive inverse .
Sum up , from ①②③④ You know , < Z , + > <\Z,+> <Z,+> It's a group .
Is it simple ?. Of course, if the title requires proof < Z , + > <\Z,+> <Z,+> It's an exchange group , Then add one step to prove commutativity .( Please try to prove , Just add the fifth step to the description of commutativity on the basis of the above steps to prove the Group .)
The operation here is addition , So the additive unit is 0 0 0, a a a The additive inverse of is − a -a −a .
1.2 subgroup
Because a group is an algebraic system , Algebraic systems consist of sets and operations defined on sets . Therefore, the concept of subgroup is also well understood
If < G , ∗ > <G,*> <G,∗> It's a group , H ⊆ G H\subseteq G H⊆G , < H , ∗ > <H,*> <H,∗> It's also a group , that < H , ∗ > <H,*> <H,∗> yes < G , ∗ > <G,*> <G,∗> Subgroups , Write it down as H ≤ G H≤G H≤G. among ∗ * ∗ Operation is the same operation .
Proof subgroup can also be proved by definition .
Example 2: prove < 5 Z , + > <5\Z,+> <5Z,+> It's a group < Z , + > <\Z,+> <Z,+> Subgroups . among 5 Z = { 5 k ∣ k ∈ Z } 5\Z=\text{\{}5k|k\in \Z \text{\}} 5Z={ 5k∣k∈Z}
①: because ∀ a , b ∈ 5 Z \forall a,b \in 5\Z ∀a,b∈5Z , namely a , b a,b a,b All are 5 5 5 Multiple , Obviously a + b a+b a+b still 5 5 5 Multiple . Therefore, the closeness of operation is established
②: because ∀ a , b , c ∈ 5 Z \forall a,b,c \in 5\Z ∀a,b,c∈5Z , There are ( a + b ) + c = a + ( b + c ) (a+b)+c=a+(b+c) (a+b)+c=a+(b+c) establish . Therefore, the operation is associative .
③: because ∀ a ∈ 5 Z \forall a \in 5\Z ∀a∈5Z , There are a + 0 = 0 + a = a a+0=0+a=a a+0=0+a=a , Therefore, the operation has a unitary 0 0 0 .
④: because ∀ a ∈ 5 Z \forall a \in 5\Z ∀a∈5Z , There are − a ∈ 5 Z -a \in 5\Z −a∈5Z , bring a + ( − a ) = ( − a ) + a = 0 a+(-a) =(-a)+a=0 a+(−a)=(−a)+a=0 establish . Therefore, any element in the set has an additive inverse .
Obviously , For any integer a a a , 5 a 5a 5a It's still an integer . therefore 5 Z ⊂ Z 5\Z \subset \Z 5Z⊂Z.
therefore < 5 Z , + > <5\Z,+> <5Z,+> yes < Z , + > <\Z,+> <Z,+> Subgroups .
Is it almost the same operation ?
Of course , There is another theorem for judging subgroups :
Theorem : set up H ⊆ G H \subseteq G H⊆G , < G , ∗ > <G,*> <G,∗> It's a group . if ∀ a , b ∈ H \forall a,b \in H ∀a,b∈H , a b − 1 ∈ H ab^{-1}\in H ab−1∈H Hang up . that < H , ∗ > < H,*> <H,∗> yes < G , ∗ > <G,*> <G,∗> Subgroups .
So we can prove the above question :
because < Z , + > <\Z,+> <Z,+> It's a group , set up a , b ∈ 5 Z a,b\in 5\Z a,b∈5Z , namely a , b a,b a,b All are 5 5 5 Multiple .
Again because b b b The additive inverse of is − b -b −b , because b b b yes 5 5 5 Multiple , that − b -b −b It's also 5 5 5 Multiple , a + ( − b ) a+(-b) a+(−b) It's also 5 5 5 Multiple .
therefore a + ( − b ) ∈ 5 Z a+(-b) \in 5\Z a+(−b)∈5Z , so < 5 Z , + > <5\Z,+> <5Z,+> yes < Z , + > <\Z,+> <Z,+> Subgroups .
Do you suddenly feel that the proof is still very simple ?, Proof group is to write eight part essay , Just add up the four properties ! Of course , In known G G G In the case of a group , We should also learn to use these four properties .
Let's look at two more questions to consolidate :
Example 3: set up G G G It's a group , And ∀ a ∈ G \forall a\in G ∀a∈G, There are a 2 = e a^{2}=e a2=e establish , prove G G G It's an exchange group .
set up $a,b \in G $, By group Sealing property , You know a b ∈ G , b a ∈ G ab\in G,ba\in G ab∈G,ba∈G.
So we can get a 2 = b 2 = ( a b ) 2 = e a^{2}=b^{2}=(ab)^{2}=e a2=b2=(ab)2=e, namely ( a b ) 2 = a 2 b 2 (ab)^{2}=a^{2}b^{2} (ab)2=a2b2 . ( Be careful : ( a b ) 2 = ( a b ) ( a b ) = a b a b (ab)^{2}=(ab)(ab)=abab (ab)2=(ab)(ab)=abab, General groups do not have commutativity )
Expand square , Available a b a b = a a b b abab=aabb abab=aabb , Multiply both sides by one a a a , Multiply one right b b b , You can get a 2 ( b a ) b 2 = a 2 ( a b ) b 2 a^{2}(ba)b^{2}=a^{2}(ab)b^{2} a2(ba)b2=a2(ab)b2 .
Eliminate square , Yes b a = a b ba=ab ba=ab establish , therefore G G G It's an exchange group .
Let's have a little more difficulty ( This question suggests imitating the above method , Do it yourself and see the answer )
Example 4: In groups G G G in , ∀ a , b \forall a,b ∀a,b, There are a 3 b 3 = ( a b ) 3 , a 4 b 4 = ( a b ) 4 , a 5 b 5 = ( a b ) 5 a^{3}b^{3}=(ab)^{3},a^{4}b^4=(ab)^4,a^5b^5=(ab)^{5} a3b3=(ab)3,a4b4=(ab)4,a5b5=(ab)5 , prove G G G It's an exchange group .
because a 3 b 3 = ( a b ) 3 a^{3}b^{3}=(ab)^{3} a3b3=(ab)3, therefore a ( a b ) 3 b = a ( a 3 b 3 ) b = a 4 b 4 = ( a b ) 4 = a ( b a ) 3 b a(ab)^{3}b=a(a^3b^3)b=a^{4}b^{4}=(ab)^{4}=a(ba)^{3}b a(ab)3b=a(a3b3)b=a4b4=(ab)4=a(ba)3b . namely a ( a b ) 3 b = a ( b a ) 3 b a(ab)^{3}b=a(ba)^{3}b a(ab)3b=a(ba)3b. Multiply left on both sides of the equal sign a − 1 a^{-1} a−1 , Take the right b − 1 b^{-1} b−1, available ( a b ) 3 = ( b a ) 3 (ab)^{3}=(ba)^{3} (ab)3=(ba)3 (P.S. because G G G It's a group , therefore a − 1 a^{-1} a−1 You can write directly )
Again because a 4 b 4 = ( a b ) 4 a^{4}b^{4}=(ab)^{4} a4b4=(ab)4, therefore a ( a b ) 4 b = a ( a 4 b 4 ) b = a 5 b 5 = ( a b ) 5 = a ( b a ) 4 b a(ab)^{4}b=a(a^4b^4)b=a^{5}b^{5}=(ab)^{5}=a(ba)^{4}b a(ab)4b=a(a4b4)b=a5b5=(ab)5=a(ba)4b . namely a ( a b ) 4 b = a ( b a ) 4 b a(ab)^{4}b=a(ba)^{4}b a(ab)4b=a(ba)4b. Multiply left on both sides of the equal sign a − 1 a^{-1} a−1 , Take the right b − 1 b^{-1} b−1, available ( a b ) 4 = ( b a ) 4 (ab)^{4}=(ba)^{4} (ab)4=(ba)4 . ( This step can be seen directly in the same way ).
Double right ( a b ) 3 (ab)^{3} (ab)3 Inverse element ( namely ( a b ) − 3 (ab)^{-3} (ab)−3), obtain ( a b ) 4 ( a b ) − 3 = ( b a ) 4 ( a b ) − 3 (ab)^{4}(ab)^{-3}=(ba)^{4}(ab)^{-3} (ab)4(ab)−3=(ba)4(ab)−3 , namely ( a b ) 4 ( a b ) − 3 = ( b a ) 4 ( b a ) − 3 (ab)^{4}(ab)^{-3}=(ba)^{4}(ba)^{-3} (ab)4(ab)−3=(ba)4(ba)−3, That is to say a b = b a ab=ba ab=ba , Reason group G G G It's an exchange group .
Here's another reminder , The power here is the abbreviation of the same operation for consecutive times , Not necessarily multiplication . For example, in addition Group < R , + > <\R,+> <R,+> in , 4 3 4^{3} 43 Three 4 4 4 Add up , So the result is 12 12 12. But in multiplicative groups < R − 0 , × > <\R-{0},×> <R−0,×> in , 4 3 4^{3} 43 It means three 4 4 4 Multiply , The result is 64 64 64 .
2 Normal subgroups and quotient groups
2.1 Simply understand coset 、 Quotient set 、 Normal subgroup 、 Quotient group
8.2 section , The textbook is confusing .... Let's first look at how coset is defined in the textbook :
Similar to the classification of modular congruence , People can pass G G G Subgroups H H H To the group G G G To classify
a H = { c ∣ c ∈ G , c − 1 a ∈ H } aH=\{c|c\in G,c^{-1}a\in H\} aH={ c∣c∈G,c−1a∈H}
So let's talk about what cosets are . Coset is A collection . $ 5\Z$ yes Z \Z Z Subgroups , The algorithm is addition . Then we can export Z \Z Z On 5 Z 5\Z 5Z The cosets of are .
5 Z , 1 + 5 Z , 2 + 5 Z , 3 + 5 Z , 4 + 5 Z 5\Z,1+5\Z,2+5\Z,3+5\Z,4+5\Z 5Z,1+5Z,2+5Z,3+5Z,4+5Z
among 1 + 5 Z = { . . . , − 4 , 1 , 6 , 11 , . . . } 1+5\Z=\{...,-4,1,6,11,...\} 1+5Z={ ...,−4,1,6,11,...}, 2 + 5 Z = { . . . , − 3 , 2 , 7 , 12 , . . . } 2+5\Z=\{...,-3,2,7,12,...\} 2+5Z={ ...,−3,2,7,12,...} , And so on . exactly , It has something to do with congruence ...
above 5 5 5 In a collection , Only 5 Z 5\Z 5Z The addition on forms a group , Additions on other sets do not form groups !!!( Because it doesn't satisfy the closeness )
Then the quotient set is A set of all cosets , Its essence is A collection of collections . Z / 5 Z \Z/5\Z Z/5Z The result is to add braces to all the previous line ..
Z / 5 Z = { 5 Z , 1 + 5 Z , 2 + 5 Z , 3 + 5 Z , 4 + 5 Z } \Z/5\Z=\{5\Z,1+5\Z,2+5\Z,3+5\Z,4+5\Z\} Z/5Z={ 5Z,1+5Z,2+5Z,3+5Z,4+5Z}
Please try to write R / Z \R/\Z R/Z Result ( answer :$ {a+\Z|a\in[0,1) }$).
And then we'll find out : Z / 5 Z \Z/5\Z Z/5Z It's also a collection ( It contains 5 5 5 Elements , Each element is a module 5 5 5 Congruence class of ). If we define operations $\bigoplus_5 $ For the mould 5 5 5 Add , Then it can be proved that : < Z / 5 Z , ⨁ 5 > <\Z/5\Z,\bigoplus_5 > <Z/5Z,⨁5> It's a group . let me put it another way , Z / 5 Z \Z/5\Z Z/5Z It also forms a group .
Because we came to the conclusion at the beginning , When the operation is addition , Z \Z Z It's a group , 5 Z 5\Z 5Z It's also a group , And quotient set Z / 5 Z \Z/5\Z Z/5Z It can also form groups . Then we can draw two conclusions :
Because the quotient set Z / 5 Z \Z/5\Z Z/5Z Can form a group , therefore
① 5 Z 5\Z 5Z yes Z \Z Z Normal subgroups of
② Z / 5 Z \Z/5\Z Z/5Z It's a Z \Z Z A quotient group on
Let's make it clear here : Z / 5 Z \Z/5\Z Z/5Z Follow Z 5 \Z_5 Z5 It's a different concept , because Z 5 = { 0 , 1 , 2 , 3 , 4 } \Z_5 =\{0,1,2,3,4\} Z5={ 0,1,2,3,4} , and Z / 5 Z = { 5 Z , 5 Z + 1 , 5 Z + 2 , 5 Z + 3 , 5 Z + 4 } \Z/5\Z=\{5\Z,5\Z+1,5\Z+2,5\Z+3,5\Z+4\} Z/5Z={ 5Z,5Z+1,5Z+2,5Z+3,5Z+4} . The elements in the former are numbers , The element in the latter is aggregate .
2.2 Relevant proof methods
1. Prove that two cosets are equal
Properties of cosets : H H H yes G G G Subsets on , a , b ∈ G a,b\in G a,b∈G . So there are :
① a H = b H ⇔ b − 1 a ∈ H aH=bH\Leftrightarrow b^{-1}a\in H aH=bH⇔b−1a∈H
② a H ∩ b H = ϕ ⇔ b − 1 a ∉ H aH\cap bH=\phi \Leftrightarrow b^{-1}a \not \in H aH∩bH=ϕ⇔b−1a∈H.
③ Any two cosets are either equal , Or not . That is to say a H ∩ b H = ϕ aH \cap bH=\phi aH∩bH=ϕ or a H = b H aH=bH aH=bH, No other relationship
for instance : 4 + 5 Z = 9 + 5 Z 4+5\Z=9+5\Z 4+5Z=9+5Z, because − 9 + 4 = − 5 ∈ 5 Z -9+4=-5\in 5\Z −9+4=−5∈5Z . and 4 + 5 Z ≠ 3 + 5 Z 4+5\Z \not=3+5\Z 4+5Z=3+5Z , because $-3+4=1 \not \in 5\Z $.
2. Prove a subgroup H H H It's a group G G G Normal subgroups of
Proof method of normal subgroup :
set up a ∈ G a\in G a∈G, H H H yes G G G Subgroups , If we want to prove H H H yes G G G Normal subgroups of , Just prove
a H a − 1 ⊂ H aHa^{-1} \subset H aHa−1⊂H
Of course, there is another property , Readers can try to prove , This conclusion is better not to use directly , Because one head can come out
if G G G It's an exchange group , H H H yes G G G Subgroups , be H H H It must be G G G Normal subgroups of
Let's take an example :
Example 5: set up G G G It's a group , C = { a ∣ a ∈ G , ∀ b ∈ G → a b = b a } C=\{a|a\in G,\forall b\in G \rightarrow ab=ba\} C={ a∣a∈G,∀b∈G→ab=ba}. prove C C C yes G G G Normal subgroups of .
First prove that C C C yes G G G Subgroups :
①: because G G G It's a group , so G G G There's a dollar on it e e e , And ∀ g ∈ G \forall g\in G ∀g∈G There are g e = e g = g ge=eg=g ge=eg=g , therefore e ∈ C e\in C e∈C . C C C There's a dollar on it e e e .
②: because G G G It's a group , so G G G The operations in are associative , C C C yes G G G Subset , Therefore, the combination of this operation is C C C China is still established
③: set up s , t ∈ C , g ∈ G s,t \in C,g\in G s,t∈C,g∈G that ( s t ) g = s ( t g ) = s ( g t ) = ( s g ) t = g s t = g ( s t ) (st)g=s(tg)=s(gt)=(sg)t=gst=g(st) (st)g=s(tg)=s(gt)=(sg)t=gst=g(st) , explain s t ∈ C st\in C st∈C , It can be seen that the operation is in C C C It is also closed .
( notes : here s t g = s g t stg=sgt stg=sgt It's using C C C Properties of the upper element , have a look C C C How are the elements defined in , since t ∈ C , g ∈ G t\in C,g\in G t∈C,g∈G, that t g = g t tg=gt tg=gt Is established , The reason for changing brackets at will is G G G It's a group , G G G The combination of is established )
④: set up s ∈ C , g ∈ G s\in C,g\in G s∈C,g∈G , from s g = g s sg=gs sg=gs , be s − 1 ( s g ) s − 1 = s − 1 ( g s ) s − 1 s^{-1}(sg)s^{-1}=s^{-1}(gs) s^{-1} s−1(sg)s−1=s−1(gs)s−1 , That is to say g s − 1 = s − 1 g gs^{-1}=s^{-1}g gs−1=s−1g ( Please go to the brackets and have a look ) , You know s − 1 ∈ C s^{-1} \in C s−1∈C.
from ①②③④ You know , C C C It's a group , And C C C yes G G G Subgroups . The following proof C C C yes G G G Normal subgroups of
set up g ∈ G , s ∈ C g\in G,s\in C g∈G,s∈C , Then there are g s g − 1 = ( g s ) g − 1 = ( s g ) g − 1 = s gsg^{-1} = (gs)g^{-1} =(sg)g^{-1}=s gsg−1=(gs)g−1=(sg)g−1=s , explain g s g − 1 ∈ C gsg^{-1} \in C gsg−1∈C , namely g C g − 1 ⊂ C gCg^{-1} \subset C gCg−1⊂C . You know C C C yes G G G Normal subgroups of .
In the above question , You will find proof C C C yes G G G Subgroups of are still defined , Four step proof . And prove C C C yes G G G Normal subgroups of , It is proved by definition . So the definition is the most important .
3 Homomorphism and isomorphism
3.1 Definition
The book defines homomorphism and isomorphism in this way :
set up f f f It's a group G G G To the group G ′ G' G′ Mapping / function , if ∀ a , b ∈ G \forall a,b\in G ∀a,b∈G , There are f ( a ) f ( b ) = f ( a b ) f(a)f(b)=f(ab) f(a)f(b)=f(ab) Hang up , be f f f yes G G G To G ′ G' G′ Homomorphism of .
Specifically , if f f f If it is injective, it is simple homomorphism , f f f Is a surjection is a full homomorphism . if f f f It is both simple homomorphism and full homomorphism , be f f f It's isomorphic .
P.S: One shot is a one-to-one mapping , Using symbolic language is : if f ( x 1 ) = f ( x 2 ) f(x_1)=f(x_2) f(x1)=f(x2) , There must be x 1 = x 2 x_1=x_2 x1=x2 . A surjection is a mapping / The value range of the function fills the whole G ′ G' G′ aggregate , That is to say, for any y ∈ G ′ y \in G' y∈G′ , There is always x ∈ G x\in G x∈G , bring y = f ( x ) y=f(x) y=f(x) establish .
for instance : set up f f f yes R \R R To R \R R Mapping , be f ( x ) = e x f(x)=e^{x} f(x)=ex It's a single shot but not a full shot , f ( x ) = x sin x f(x)=x\sin x f(x)=xsinx It's a full shot, but not a single shot , f ( x ) = x 3 f(x)=x^{3} f(x)=x3 It's both a single shot and a full shot , f ( x ) = sin x f(x)=\sin x f(x)=sinx Neither single shot nor full shot .
3.2 Method of proof
So we get the proof of homomorphism and isomorphism ( It's still the definition ):
Methods of proving homomorphism : Find one from G G G To G ′ G' G′ Function of f f f, To prove to G G G Arbitrary in a , b a,b a,b , There are f ( a b ) = f ( a ) f ( b ) f(ab)=f(a)f(b) f(ab)=f(a)f(b) establish .
Methods of proving isomorphism : Find one from G G G To G ′ G' G′ Function of f f f, Prove that this function has :① Homomorphism ,② Single shot ,③ Full shot . Three fixed steps , Just like proving that groups have four fixed steps .
Of course , There are several properties that need to be understood , It can be used directly :
if f f f Is a group homomorphism , There must be f ( e ) = e ′ f(e)=e' f(e)=e′ , f ( a k ) = [ f ( a ) ] k f(a^{k})=[f(a)]^{k} f(ak)=[f(a)]k It's all established .
The necessary and sufficient condition of injectivity : ker f = { e } \ker f=\{e\} kerf={ e} . The necessary and sufficient condition of surjection : f ( G ) = G ′ f(G)=G' f(G)=G′
There are still a few concepts to understand :
Homomorphic kernel k e r f = { x ∣ x ∈ G And f ( x ) = e ′ } \mathrm{ker} f=\{x|x\in G And f(x)=e'\} kerf={ x∣x∈G And f(x)=e′} ( e ′ e' e′ It's a group G ′ G' G′ One yuan of ). for example : from < Z , + > <\Z,+> <Z,+> To < Z 5 , ⨁ 5 > <\Z_{5},\bigoplus_5 > <Z5,⨁5> Mapping on f ( x ) = x m o d 5 f(x)=x\mod 5 f(x)=xmod5 . Obviously , f ( a ) ⨁ 5 f ( b ) = f ( a + b ) f(a)\bigoplus_5 f(b)=f(a+b) f(a)⨁5f(b)=f(a+b) Is established . So this is a homomorphism . and Z 5 \Z_5 Z5 The unit in is 0 0 0 , So we want to have 0 = f ( x ) 0=f(x) 0=f(x) , So we can get x ∈ 5 Z = { 5 k ∣ k ∈ Z } x\in 5\Z=\{5k|k\in Z\} x∈5Z={ 5k∣k∈Z} . So here , k e r f = 5 Z \mathrm{ker}f=5\Z kerf=5Z .
Please pay attention to the Z 5 \Z_{5} Z5 and 5 Z 5\Z 5Z The difference between ( As mentioned above ), as well as Z \Z Z Upper operation and Z 5 \Z_{5} Z5 The difference of upper operation , above a , b a,b a,b yes Z \Z Z Medium element , f ( a ) , f ( b ) f(a),f(b) f(a),f(b) yes Z 5 \Z_{5} Z5 Medium element .
Fundamental theorem of homomorphism : if f f f yes G G G To G ′ G' G′ The homomorphism of , be G / k e r f G/\mathrm{ker}f G/kerf And G ′ G' G′ isomorphism
Example 6: Prove the basic theorem of homomorphism
set up F F F yes G / k e r f G/\mathrm{ker}f G/kerf To G ′ G' G′ Mapping , F ( a ker f ) = f ( a ) F(a\ker f)=f(a) F(akerf)=f(a)
①: prove F F F It's homomorphism : because f f f It's homomorphism , therefore f ( a b ) = f ( a ) f ( b ) f(ab)=f(a)f(b) f(ab)=f(a)f(b) , therefore F ( a ker f ) F ( b ker f ) = F ( a b ker f ) F(a\ker f)F(b\ker f)=F(ab\ker f) F(akerf)F(bkerf)=F(abkerf) establish , so F F F It's homomorphism .
②: prove F F F It's a single shot : if a ker F ∈ ker F a\ker F \in \ker F akerF∈kerF , So there are F ( a ker f ) = f ( a ) = e ′ F(a\ker f)=f(a)=e' F(akerf)=f(a)=e′ . therefore a ∈ ker f a\in \ker f a∈kerf , so a ker f = ker f a\ker f=\ker f akerf=kerf. So we have ker F = { ker f } \ker F =\{\ker f\} kerF={ kerf} . ker F \ker F kerF There is only one element in , so F F F It's a single shot .
③: because f f f It's homomorphism , So for any y ∈ G ′ y\in G' y∈G′, There is always x ∈ G x\in G x∈G bring y = f ( x ) y=f(x) y=f(x). So we have F ( x ker f ) = y F(x\ker f)=y F(xkerf)=y establish , so F F F It's a volley .
from ①②③ You know : F F F It's a volley , so G / k e r f G/\mathrm{ker}f G/kerf And G ′ G' G′ isomorphism .
It is worth noting that : G / ker f G/\ker f G/kerf It's a set of sets , therefore F F F The domain of definition yes G / ker f G/\ker f G/kerf The elements in ( The type of this element is set ), The value range is G ′ G' G′ The elements in .
Let's take another example to prove isomorphism
Example 7: set up G G G It's a group , a ∈ G a\in G a∈G , f ( x ) = a x a − 1 f(x)=axa^{-1} f(x)=axa−1 . prove f f f yes G G G To G G G Automorphism of .
①: Prove homomorphism : set up s , t ∈ G s,t\in G s,t∈G , be f ( s ) f ( t ) = a s a − 1 a t a − 1 = a s ( a a − 1 ) t a − 1 = a s t a − 1 = f ( s t ) f(s)f(t)=asa^{-1}ata^{-1}=as(aa^{-1})ta^{-1}=asta^{-1}=f(st) f(s)f(t)=asa−1ata−1=as(aa−1)ta−1=asta−1=f(st) , therefore f f f Have homomorphism .
②: Prove that single shot : set up f ( x 1 ) = f ( x 2 ) f(x_1)=f(x_2) f(x1)=f(x2) , namely a x 1 a − 1 = a x 2 a − 1 ax_1a^{-1}=ax_2a^{-1} ax1a−1=ax2a−1, Multiply both sides by one a − 1 a^{-1} a−1, Multiply one right a a a , You can get a − 1 a x 1 a − 1 a = a − 1 a x 2 a − 1 a a^{-1}ax_1a^{-1}a=a^{-1}ax_2a^{-1}a a−1ax1a−1a=a−1ax2a−1a , namely x 1 = x 2 x_1=x_2 x1=x2 establish . so f f f It's a single shot .
③: Prove the full shot : set up y = f ( x ) = a x a − 1 y=f(x)=axa^{-1} y=f(x)=axa−1 , be a − 1 y a = x a^{-1}ya=x a−1ya=x , namely y = f ( a − 1 y a ) y=f(a^{-1}ya) y=f(a−1ya) , so f f f It's a volley .
Because the operations in the group are closed , So ①②③ You know , f f f yes G G G To G ′ G' G′ Automorphism of .
~~ So proving isomorphism is still writing eight part essay .~~ Directly use the definition of a shuttle .
4. Cyclic groups
4.1 Several definitions
set up G G G It's a group
G G G Medium element a a a The order of o r d ( a ) \mathrm{ord}(a) ord(a) : send a k = e a^{k}=e ak=e The smallest positive integer of k k k , And k k k It must be ∣ G ∣ |G| ∣G∣ The factor of
if G G G There is an element in g g g , send G = { g , g 2 , g 3 , . . . } G=\{g,g^2,g^3,...\} G={ g,g2,g3,...} , be G G G It's a cyclic group , g g g yes G G G The generator of .( Analog primal root )
Properties of cyclic groups :
Cyclic groups must be commutative groups
Infinite order cyclic groups and < Z , + > <\Z,+> <Z,+> isomorphism , Finite order ( n n n rank ) Cyclic groups and < Z n , ⨁ n > <\Z_n,\bigoplus_n> <Zn,⨁n> isomorphism .
if g g g It's a group G G G The generator of , if ∣ G ∣ = + ∞ |G|=+∞ ∣G∣=+∞, be G G G There are only two generators g g g and g − 1 g^{-1} g−1 . if ∣ G ∣ = n |G|=n ∣G∣=n , g k ∣ gcd ( k , n ) = 1 g^{k}|_{\gcd(k,n)=1} gk∣gcd(k,n)=1 yes G G G The generator of .
Please try to prove it yourself : < Z 41 ∗ , ⨂ 41 > <\Z_{41}^*,\bigotimes_{41}> <Z41∗,⨂41> And < Z 40 , ⨁ 40 > <\Z_{40},\bigoplus_{40}> <Z40,⨁40> These two groups are isomorphic , among ⨂ 41 \bigotimes_{41} ⨂41 Is the mould 41 41 41 Multiplication , ⨁ 40 \bigoplus_{40} ⨁40 Is the mould 40 40 40 Add .
Tips : model 41 41 41 A primitive root of is 6 6 6 .
answer : set up f f f yes Z 40 \Z_{40} Z40 To Z 41 ∗ \Z_{41}^* Z41∗ The function on , f ( x ) = 6 x m o d 41 f(x)=6^{x} \mod {41} f(x)=6xmod41
①: because φ ( 41 ) = 40 \varphi(41) = 40 φ(41)=40. set up a , b ∈ Z 40 a,b\in \Z_{40} a,b∈Z40. so f ( a + b ) = 6 a ⨁ 40 b m o d 41 = 6 a ⨂ 41 6 b = f ( a ) ⨂ 41 f ( b ) f(a+b)= 6^{a\bigoplus_{40}b}\mod 41=6^a\bigotimes_{41}6^b=f(a)\bigotimes_{41}f(b) f(a+b)=6a⨁40bmod41=6a⨂416b=f(a)⨂41f(b), so f f f Have homomorphism .
②: if f ( x 1 ) = f ( x 2 ) f(x_1)=f(x_2) f(x1)=f(x2), namely 6 x 1 ≡ 6 x 2 ( m o d 41 ) 6^{x_1}\equiv 6^{x_2} \pmod{41} 6x1≡6x2(mod41) . therefore x 1 ≡ x 2 ( m o d 40 ) x_1\equiv x_2 \pmod {40} x1≡x2(mod40). Again because x 1 , x 2 ∈ Z 40 x_1,x_2 \in \Z_{40} x1,x2∈Z40 , So only x 1 = x 2 x_1=x_2 x1=x2 establish , so f f f It's a single shot .
③: because 6 6 6 Is the mould 41 41 41 The original root , so model 41 41 41 A complete remainder system of can be written as { 6 , 6 2 , 6 3 , . . . , 6 40 = 6 0 = 1 } \{6,6^{2},6^{3},...,6^{40}=6^0=1\} { 6,62,63,...,640=60=1} , namely 6 i , i ∈ Z 40 6^{i},i\in \Z_{40} 6i,i∈Z40 Traversed the module 41 41 41 The complete residue system of , so f f f It's a volley .
from ①②③ You know , < Z 41 ∗ , ⨂ 41 > <\Z_{41}^*,\bigotimes_{41}> <Z41∗,⨂41> And < Z 40 , ⨁ 40 > <\Z_{40},\bigoplus_{40}> <Z40,⨁40> These two groups are isomorphic
4.2 Method of proof
Prove that a group is a cyclic group , Is to find it The generator , If it is a finite cyclic group ( The steps are n n n ), Find an order of n n n The elements of .
example 7: Prove that a group of prime order must be a cyclic group
set up ∣ G ∣ = p |G|=p ∣G∣=p Prime number , Then for groups G G G Any element in , The order can only be 1 1 1 or p p p .
set up a ≠ e a \not = e a=e , be a a a The order of cannot be 1 1 1 , So only a a a The first step is p p p . therefore a a a It's a group $G $ The generator of , G G G It's a cyclic group
example 8: Known group G G G, ∣ G ∣ = p q |G|=pq ∣G∣=pq , among p , q p,q p,q Are different primes , prove G G G It's a cyclic group .
prove : because ∣ G ∣ = p q |G|=pq ∣G∣=pq, p , q p,q p,q Are different primes , So for any element a a a, a a a The order of can only be 1 , p , q , p q 1,p,q,pq 1,p,q,pq Four situations . if a ≠ e a\not =e a=e, be a a a The order of can only be p , q , p q p,q,pq p,q,pq.
set up g , h ∈ G g,h\in G g,h∈G, o r d ( g ) = p , o r d ( h ) = q \mathrm{ord}(g)=p,\mathrm{ord}(h)=q ord(g)=p,ord(h)=q . Because group G G G The closeness of operations in , so g h ∈ G gh\in G gh∈G .
Then there are ( g h ) 1 ≠ e (gh)^{1}\not =e (gh)1=e, ( g h ) p = g p h p = h p ≠ e (gh)^{p}=g^ph^p=h^p\not =e (gh)p=gphp=hp=e, ( g h ) q = g q h q ≠ e (gh)^{q}=g^qh^q\not =e (gh)q=gqhq=e, explain ( g h ) (gh) (gh) The order of cannot be 1 , p , q 1,p,q 1,p,q.
so o r d ( g h ) = p q = ∣ G ∣ \mathrm{ord}(gh)=pq=|G| ord(gh)=pq=∣G∣. g h gh gh yes G G G The generator of , Reason group G G G It's a cyclic group .
Do you feel a little confused ? Then I'll take a big move !.
5 Summary of ideas of proof questions in group theory
a a a The order of can only be p , q , p q p,q,pq p,q,pq.
set up g , h ∈ G g,h\in G g,h∈G, o r d ( g ) = p , o r d ( h ) = q \mathrm{ord}(g)=p,\mathrm{ord}(h)=q ord(g)=p,ord(h)=q . Because group G G G The closeness of operations in , so g h ∈ G gh\in G gh∈G .
Then there are ( g h ) 1 ≠ e (gh)^{1}\not =e (gh)1=e, ( g h ) p = g p h p = h p ≠ e (gh)^{p}=g^ph^p=h^p\not =e (gh)p=gphp=hp=e, ( g h ) q = g q h q ≠ e (gh)^{q}=g^qh^q\not =e (gh)q=gqhq=e, explain ( g h ) (gh) (gh) The order of cannot be 1 , p , q 1,p,q 1,p,q.
so o r d ( g h ) = p q = ∣ G ∣ \mathrm{ord}(gh)=pq=|G| ord(gh)=pq=∣G∣. g h gh gh yes G G G The generator of , Reason group G G G It's a cyclic group .
Do you feel a little confused ? Then I'll take a big move !.
5 Summary of ideas of proof questions in group theory
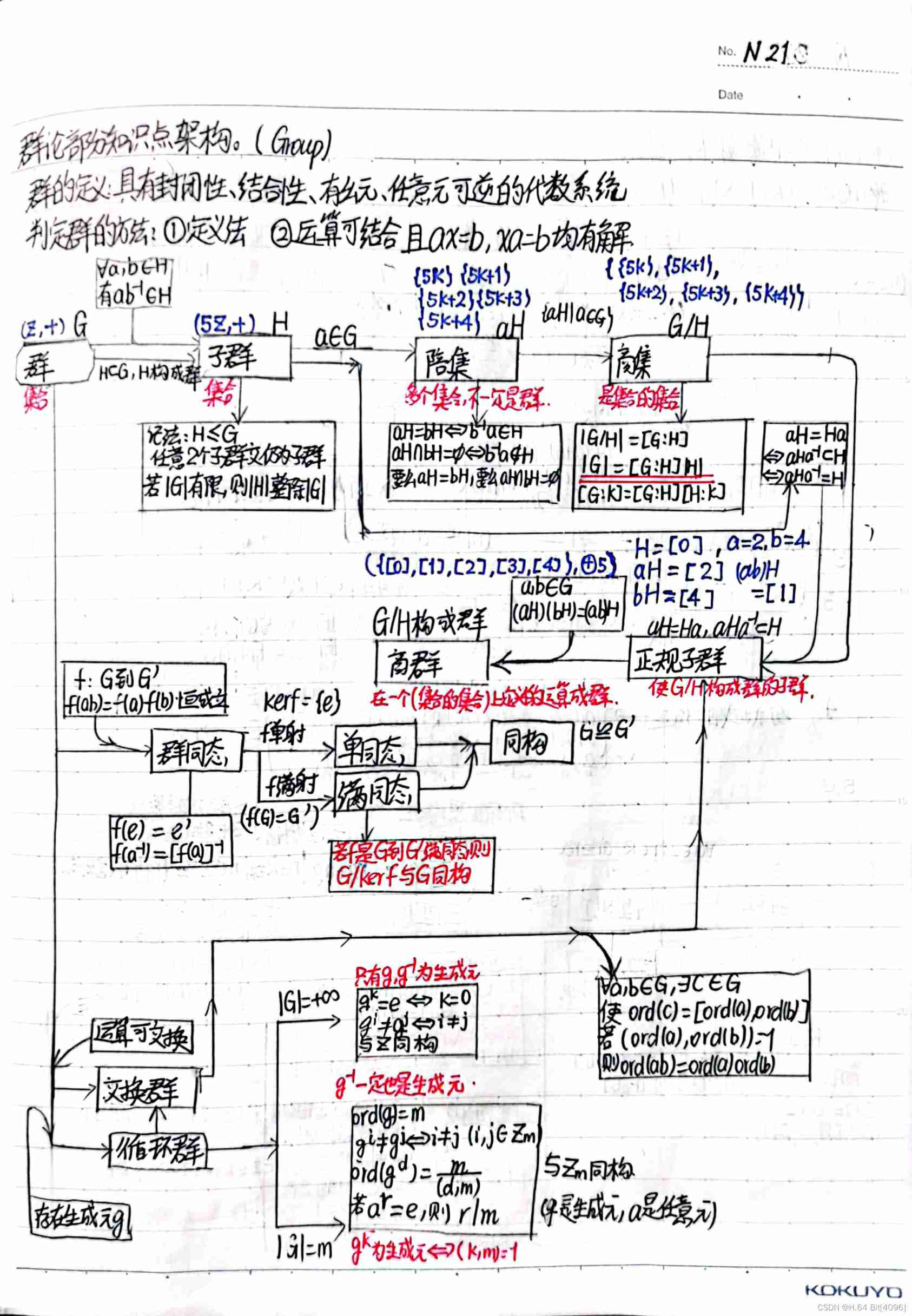
边栏推荐
- A detailed explanation of ASCII code, Unicode and UTF-8
- Go array and slice
- Go pointer
- restTemplate详解
- Shandong University Summer Training - 20220620
- [深度学习论文笔记]TransBTSV2: Wider Instead of Deeper Transformer for Medical Image Segmentation
- Catch all asynchronous artifact completable future
- 面试官灵魂拷问:为什么代码规范要求 SQL 语句不要过多的 join?
- Solve the problem of "unable to open source file" xx.h "in the custom header file on vs from the source
- Zhubo Huangyu: these spot gold investment skills are not really bad
猜你喜欢

MySQL --- 数据库查询 - 排序查询、分页查询
Huawei push service content, read notes
Win10 - lightweight gadget
ZABBIX monitoring
![[server data recovery] a case of RAID5 data recovery stored in a brand of server](/img/04/c9bcf883d45a1de616c4e1b19885a5.png)
[server data recovery] a case of RAID5 data recovery stored in a brand of server
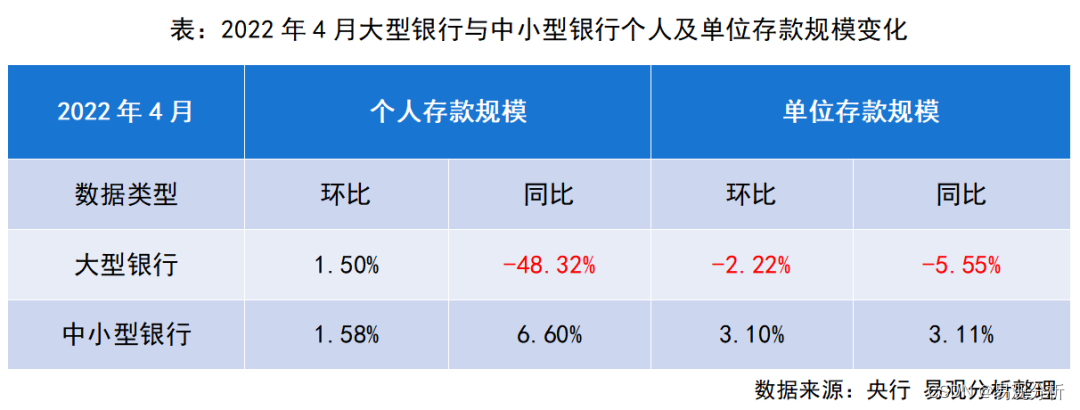
Although the volume and price fall, why are the structural deposits of commercial banks favored by listed companies?
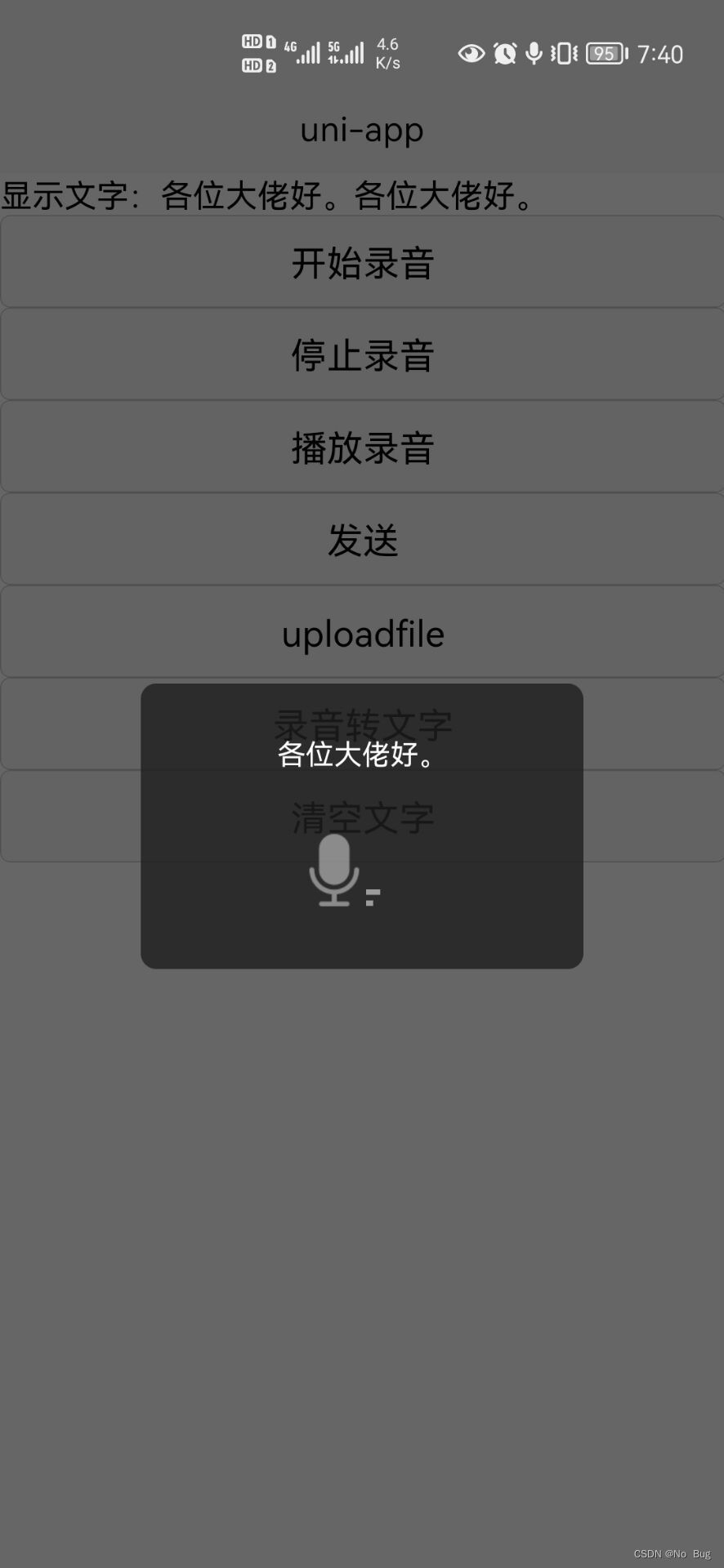
The development of speech recognition app with uni app is simple and fast.
Jenkins installation
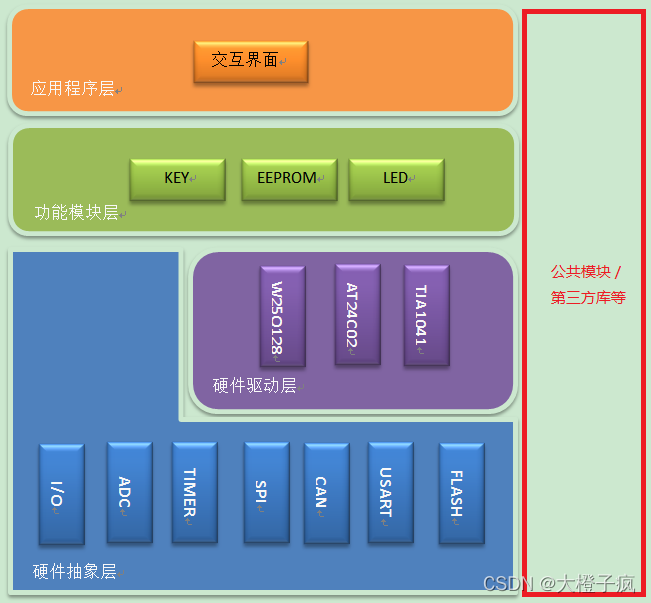
嵌入式软件架构设计-消息交互
![[daily question] 1200 Minimum absolute difference](/img/2f/9214df63f6d5fafa1f7247c4529643.png)
[daily question] 1200 Minimum absolute difference
随机推荐
龙芯派2代烧写PMON和重装系统
Binder communication process and servicemanager creation process
"Baidu Cup" CTF competition in September, web:sql
【Hot100】33. Search rotation sort array
Summit review | baowanda - an integrated data security protection system driven by compliance and security
Programmer growth Chapter 8: do a good job of testing
Huawei push service content, read notes
Difference between avc1 and H264
asp. Net read TXT file
Zhubo Huangyu: these spot gold investment skills are not really bad
华为推送服务内容,阅读笔记
Could not set property ‘id‘ of ‘class XX‘ with value ‘XX‘ argument type mismatch 解决办法
Idea remote debugging agent
Go array and slice
Wonderful express | Tencent cloud database June issue
MySQL - database query - sort query, paging query
When using Tencent cloud for the first time, you can only use webshell connection instead of SSH connection.
Intranet penetration tool NetApp
The real king of caching, Google guava is just a brother
jasypt配置文件加密|快速入门|实战