当前位置:网站首页>【刷题】BFS题目精选
【刷题】BFS题目精选
2022-07-05 03:38:00 【影中人lx】
文章目录
1.BFS使用场景
分层遍历
一层一层的遍历一个图、数、矩阵
简单图的最短路径
连通块问题
通过图的一个点找到其他所有连通的点
找到所有方案问题的一种非递归实现方式
拓扑排序
时间复杂度:
N个点,M条边,图上BFS时间复杂度 = O(N + M),说是 O(M)问题也不大,因为M一般都比N大。
M最大是 O(N^2) 的级别(任意两个点之间都有边), 所以最坏情况可能是 O(N^2)
1.1.关于最短路算法
1.1.1dijkstra算法
也叫做单源最短路径算法,解决一个点到其余个点顶点的最短路径
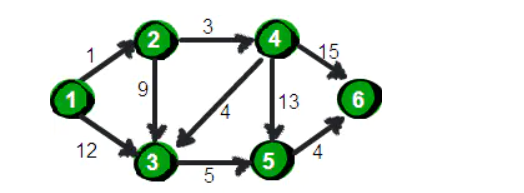
首先需要写出邻接矩阵

使用dis数组存储源顶点(1号顶点)到其余个顶点的距离
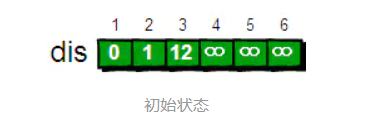
具体思路
从初始的dis数组中找到最小值为2,那么1->2顶点的最短路径就成为了确定值,值为1。
从顶点2开始出发,可以到达的顶点为2->3,2->4;其中如果中顶点2进行"中转",那么1->2->3的路径为1(1->2的最短路径)+9(2->3的路径)为10,小于1->3的距离12,所以将dis数组中1->3的值变为10;对2->4进行同样的处理1->4的最短路径更新为4。
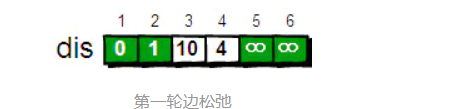
在现在的dis数组中,确定的顶点有2;而第一次松弛后除去到顶点2的最短路径为1->4(路径长度为4),顶点4为确定值。从4开始出发
- 可以到达的顶点有3,5,6;将顶点4作为"中转"进行第二轮的松弛
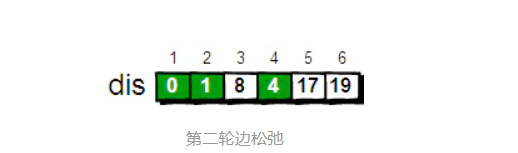
现在的确定的顶点为2,4;剩下顶点的最短路径为1->3,顶点3为最短路径,变为确定值;
进行下一轮的松弛

最终的松弛结果为:
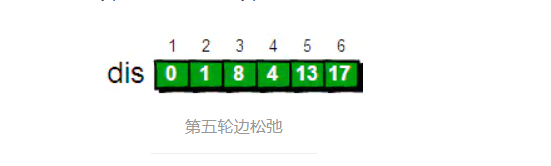
dis数组中存放了到各顶点的最短路径
//代码实现
const int INF=INT_MAX;//最大值
const int Maxsize=INT_MAX;//最大顶点数
int e[Maxsize][Maxsize];//邻接矩阵
int flag[Maxsize];//标记数组,记录顶点是否为
int dis[Maxsize];//距离表
int n,m;//n表示节点,m表示边
//初始化dis数组
void dijkstra(){
//邻接矩阵中的0位置不存数,为了方便都按照结点开始
for(int i=1;i<=n;i++){
dis[i]=e[1][i]
}
for(int i=2;i<=n;i++){
flag[i]=0;
}
book[i]=1;
//对dis进行松弛处理
for(int i=1;i<=n-1;i++){
//对于n个节点需要进行n-1次松弛处理
//记录这一轮松弛的最短距离
int min_num=INT_MAX;
//记录这一轮松弛的确定节点
int min_index=0;
for(int k=1;k<=n;k++){
if(flag[k]==0&&dis[k]<min_num)//如果还不是确定结点
{
min_num=dis[k];
min_index=k;
}
}
//确定结点
flag[min_index]=1;
//松弛处理
for(int j=1;j<=n;j++){
if(flag[j]==0&&e[min_index][j]<INT_MAX)//如果两个结点之间有路径
{
dis[j]=min(dis[j],dis[min_index]+e[min_index][j]);
}
}
}
}
dijkstra算法的优化
c edge
{
int d,v;// d:距离;v:节点(弧头)
edge(){
}
edge(int a,int b)// 初始化 d 和 v
{
d=a,v=b;
}
// 重载"<"运算符,以便更改优先队列的排序规则
// 根据"最短距离"d来进行排序
bool operator < (const edge&x)const
{
if(d==x.d)return v<x.v;
else return d>x.d;
}
};
vector<edge>G[Maxsize];// 图 G
int dis[Maxsize];// 距离表
int n,m;// n:顶点个数 m:边数
int v1,v2,w;// v1->v2,weight==w
// Dijkstra算法,源点为 s
void dijkstra(int s)
{
// 初始化dis数组
for(int i=0;i<=n;i++)dis[i]=INF;
dis[s]=0;
priority_queue<edge>que;// 优先队列
que.push(edge(dis[s],s));// 将起点压入队列
// 队列非空
while(!que.empty())
{
// get the min_index
edge temp=que.top();
que.pop();
int v=temp.v;// 顶点
if(dis[v]<temp.d)continue;//
// 遍历顶点v相连的所有边
for(int i=0;i<G[v].size();i++)
{
edge e=G[v][i];
if(dis[e.v]>dis[v]+e.d)
{
dis[e.v]=dis[v]+e.d;
que.push(edge(dis[e.v],e.v));
}
}
}
}
1.1.2Floyd-Warshall算法
弗洛伊德算法的核心就是通过引入第三k个顶点进行中转,只需要判e[ i ] [ 1 ]+e[ 1 ] [ j ]是否会比e[ i ] [ j ]小即可。
//弗洛伊德算法最核心的部分只有几行代码,其中e表示邻接矩阵
for(int k=1;k<=n;k++){
//中间媒介可能不止一个
for(int i=1;i<=n;i++){
//遍历所有的结点
for(int j=1;j<=n;j++){
e[i][j]=min(e[i][j],e[i][k]+e[j][j];)
}
}
}
弗洛伊德算法的优点是可以处理负权问题
2.题目
题目1:
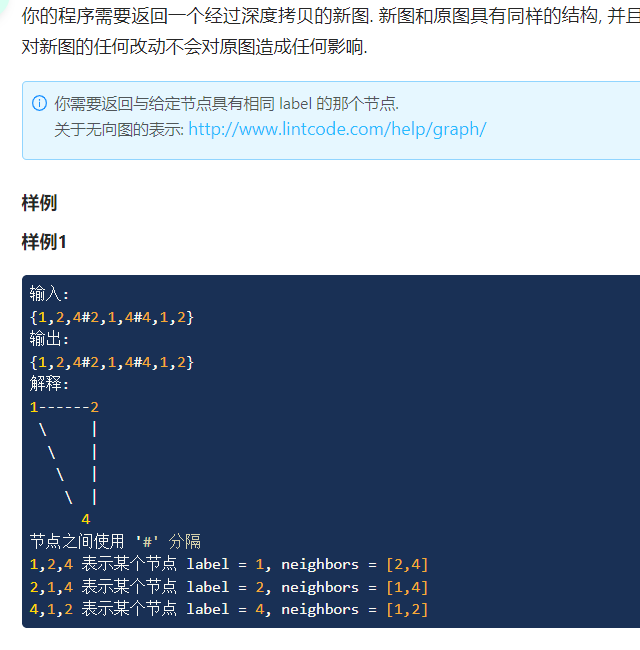
方法一:分治
class Solution {
public:
UndirectedGraphNode *clone(UndirectedGraphNode*node,map<int,UndirectedGraphNode *>&table){
if(node==NULL){
return NULL;
}
//如果当前的结点已经被复制
if(table.find(node->label)!=table.end()){
return table[node->label];
}
//如果当前结点没有被复制
//调用构造函数
UndirectedGraphNode *newcode=new UndirectedGraphNode(node->label);
table[node->label]=newcode;
for(int i=0;i<(node->neighbors).size();i++){
UndirectedGraphNode *code=clone((node->neighbors)[i],table);
(newcode->neighbors).push_back(code);
}
return newcode;
}
UndirectedGraphNode* cloneGraph(UndirectedGraphNode *node) {
map<int,UndirectedGraphNode *>visittable;
return clone(node,visittable);
}
};
方法二:BFS
//思路分为三步
//第一步:得到所有不重复的点
//第二步:将点与复制的点进行映射
//第三步:复制边
class Solution {
public:
UndirectedGraphNode* cloneGraph(UndirectedGraphNode *node) {
if(node==nullptr){
return node;
}
//第一步:得到所有的点
vector<UndirectedGraphNode*>nodes=getnodes(node);
//第二步:将得到的点和复制的点进行映射
unordered_map<UndirectedGraphNode*,UndirectedGraphNode*>mapping=clonenodes(nodes);
//第三步:连接边
connectnodes(mapping,nodes);
return mapping[node];
}
vector<UndirectedGraphNode *>getnodes(UndirectedGraphNode *node){
queue<UndirectedGraphNode *>q;
//不重复的Set
unordered_set<UndirectedGraphNode *>s;
vector<UndirectedGraphNode*>nodes;
q.push(node);
s.insert(node);
nodes.push_back(node);
while(!q.empty()){
UndirectedGraphNode*tmp=q.front();
q.pop();
for(auto neighbor:tmp->neighbors){
//如果在s中找到,表示已经被放入了则跳过
if(s.find(neighbor)!=s.end()){
continue;
}
q.push(neighbor);
s.insert(neighbor);
nodes.push_back(neighbor);
}
}
return nodes;
}
unordered_map<UndirectedGraphNode *,UndirectedGraphNode *>clonenodes(vector<UndirectedGraphNode *>nodes){
unordered_map<UndirectedGraphNode *,UndirectedGraphNode *>mapping;
for(auto node:nodes){
mapping.insert(make_pair(node,new UndirectedGraphNode(node->label)));
}
return mapping;
}
//连接复制好的边
void connectnodes(unordered_map<UndirectedGraphNode *,UndirectedGraphNode *>mapping,vector<UndirectedGraphNode *>nodes){
for(auto node:nodes){
for(auto neighbor:node->neighbors){
UndirectedGraphNode*newnode=mapping[node];
UndirectedGraphNode*newneighbor=mapping[neighbor];
newnode->neighbors.push_back(newneighbor);
}
}
}
};
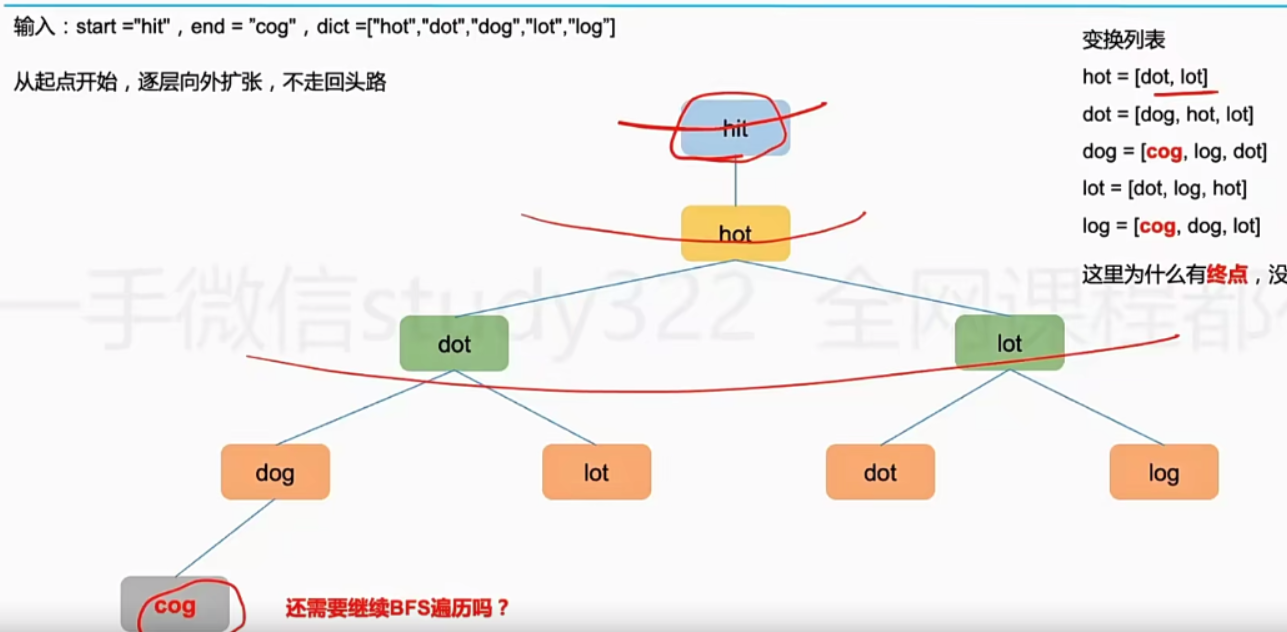
(题目2)
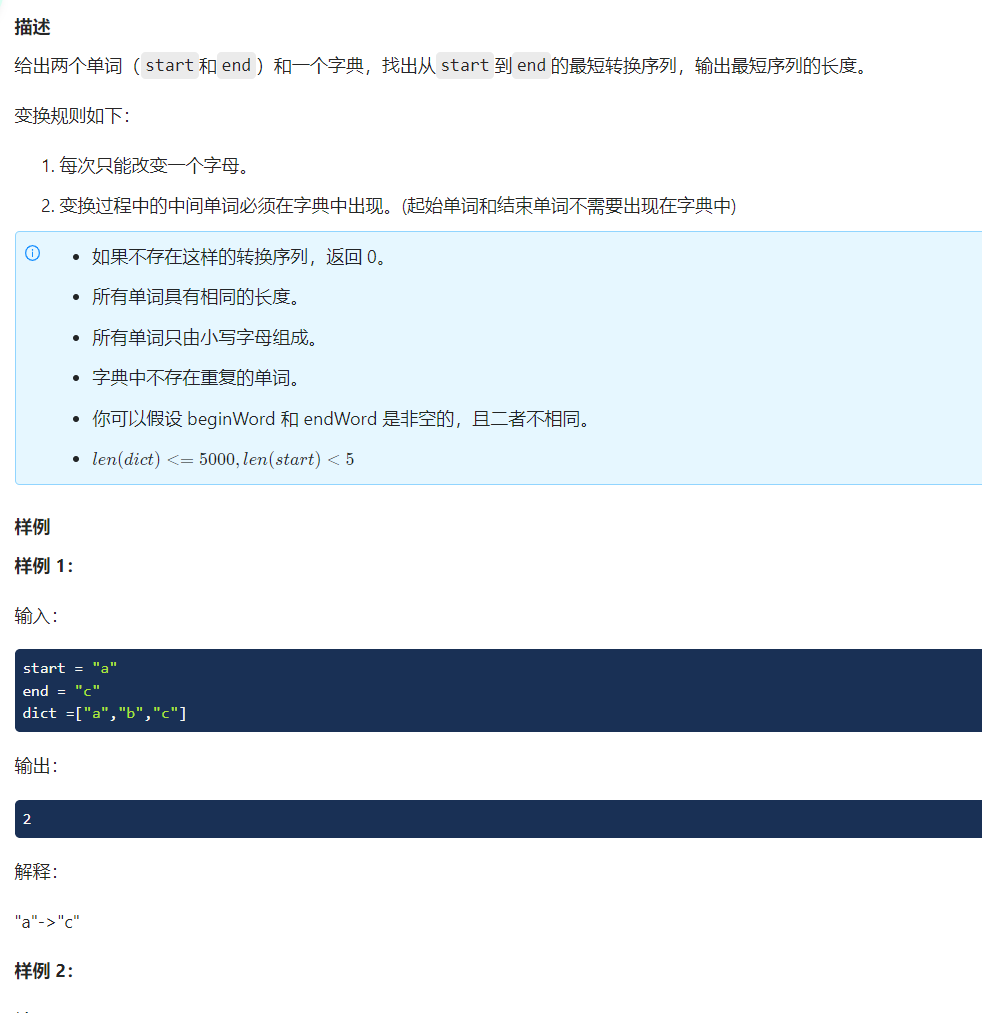
思路:
每个单词可以转换的单词形成了一棵树,所以可以使用BFS得到结果
// version LintCode
class Solution {
public:
int ladderLength(string &start, string &end, unordered_set<string> &dict) {
int n=start.size();
if(start==end){
return 1;
}
if(n<1||n!=end.size()){
return -1;
}
queue<string>q;
q.push(start);
dict.erase(start);
int step=2;
while(!q.empty()){
//记录这一层的单词数量
int size=q.size();
for(int i=0;i<size;i++){
string tmp=q.front();
q.pop();
//替换字母
for(int j=0;j<tmp.size();j++){
char ch=tmp[j];
for(char c='a';c<='z';c++){
if(ch==c){
continue;
}
tmp[j]=c;
if(tmp==end){
return step;
}
else if(dict.find(tmp)!=dict.end()){
q.push(tmp);
dict.erase(tmp);
}
tmp[j]=ch;
}
}
}
//每遍历完一次就需要加1
step++;
}
return 0;
}
};
(题目3:连通块问题)

class Solution {
public:
int numIslands(vector<vector<bool>> &grid) {
if(grid.size()==0||grid[0].size()==0){
return 0;
}
int m=grid.size(),n=grid[0].size(),num=0;
//标记数组
vector<vector<bool>>flag(m,vector<bool>(n,false));
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]&&!flag[i][j]){
dfs(grid,flag,i,j,m,n);
num++;
}
}
}
return num;
}
void dfs(vector<vector<bool>>&grid,vector<vector<bool>>&flag,int i,int j,int m,int n){
if(i<0||i>=m||j<0||j>=n||!grid[i][j]||flag[i][j]){
return ;
}
flag[i][j]=true;
dfs(grid,flag,i+1,j,m,n);
dfs(grid,flag,i-1,j,m,n);
dfs(grid,flag,i,j+1,m,n);
dfs(grid,flag,i,j-1,m,n);
}
};
(题目5)
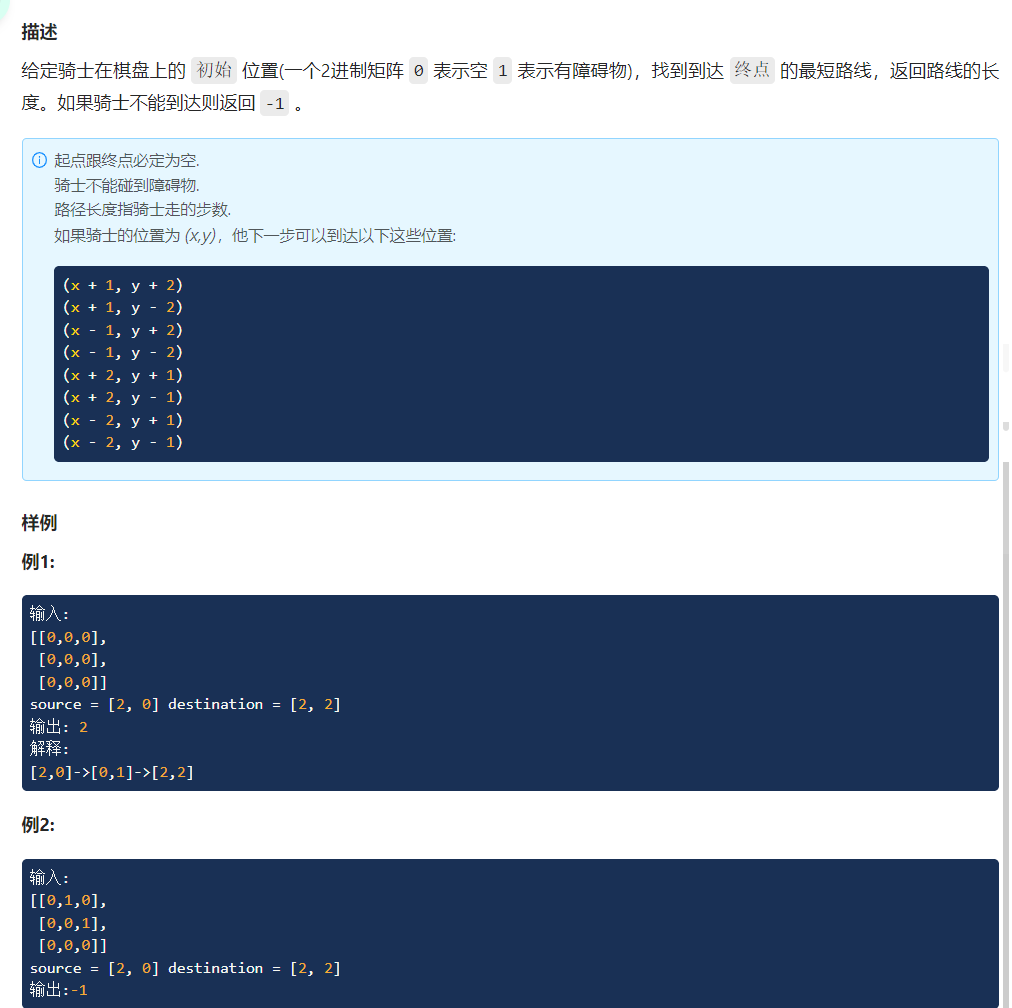
方法:BFS
BFS将达到的点按照路径转换为一棵树,模拟对树的层序遍历实现。
//朴素BFS
class Solution {
public:
int shortestPath(vector<vector<bool>> &grid, Point source, Point destination) {
int m=grid.size(),n=grid[0].size();
if(m==0||n==0){
return -1;
}
queue<Point>q;
q.push(source);
int ans=0;
vector<vector<int>>direct={
{
1,2},{
1,-2},{
-1,2},{
-1,-2},{
2,1},{
2,-1},{
-2,1},{
-2,-1}};
while(!q.empty()){
//记录这一层的数量
int size=q.size();
for(int i=0;i<size;i++){
Point tmp=q.front();q.pop();
if(tmp.x==destination.x&&tmp.y==destination.y){
return ans;
}
for(int k=0;k<8;k++){
Point node;
node.x=tmp.x+direct[k][0];
node.y=tmp.y+direct[k][1];
if(node.x>=0&&node.x<m&&node.y>=0&&node.y<n){
if(!grid[node.x][node.y]){
q.push(node);
}
grid[node.x][node.y]=true;
}
}
}
ans++;
}
return -1;
}
};
(题目6)
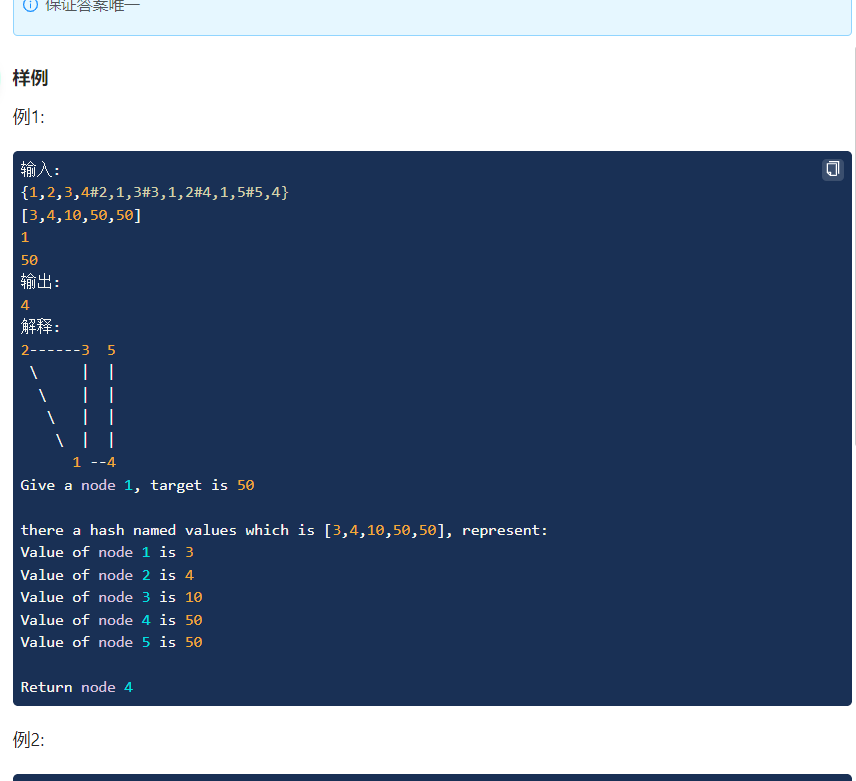
//朴素bfs
class Solution {
public:
UndirectedGraphNode* searchNode(vector<UndirectedGraphNode*>& graph,
map<UndirectedGraphNode*, int>& values,
UndirectedGraphNode* node,
int target) {
queue<UndirectedGraphNode*>q;
q.push(node);
set<UndirectedGraphNode*>se;
se.insert(node);
while(!q.empty()){
UndirectedGraphNode* tmp=q.front();q.pop();
if(values[tmp]==target)
{
return tmp;
}
for(auto it=tmp->neighbors.begin();it!=tmp->neighbors.end();it++){
if(se.find(*it)==se.end()){
se.insert(*it);
q.push(*it);
}
}
}
return NULL;
}
};
(题目7)
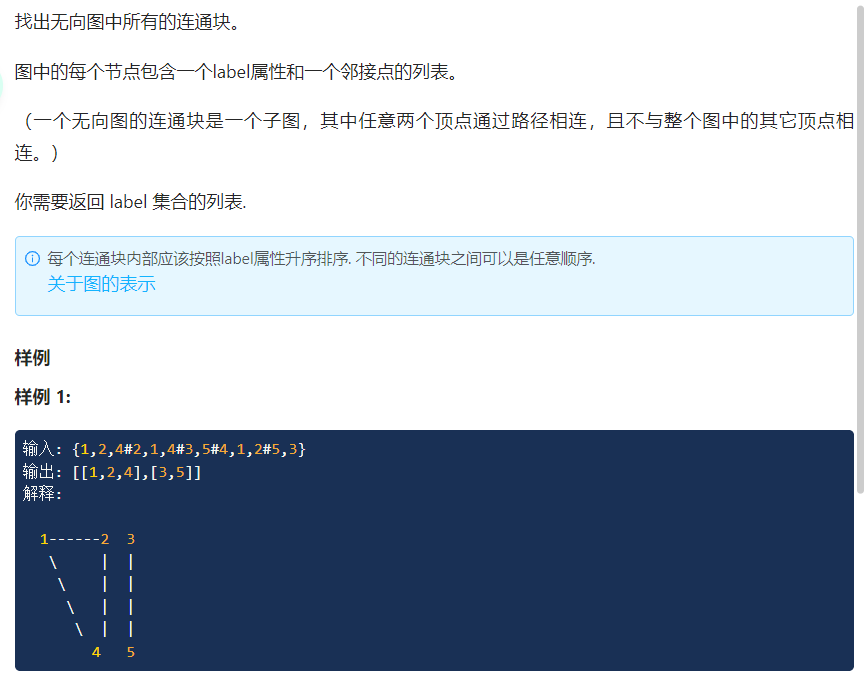
//考察点:并查集
//用map记录父亲节点
map<int,int>f;
//寻找根节点
int find(int x){
return f[x]==x?x:f[x]=find(f[x]);
}
class Solution {
public:
vector<vector<int>> connectedSet(vector<UndirectedGraphNode*> nodes) {
if(nodes.empty()){
return {
};
}
//初始化
for(int i=0;i<nodes.size();i++){
f[nodes[i]->label]=nodes[i]->label;
}
for(auto e:nodes){
//互为邻居的为同一块
for(auto i:e->neighbors){
if(find(e->label)!=find(i->label)){
f[find(i->label)]=f[find(e->label)];
}
}
}
map<int,vector<int>>tmpres;
for(auto e:nodes){
//将父节点相同的放在同一个vector中
tmpres[find(e->label)].push_back(e->label);
}
vector<vector<int>>res;
for(auto i:tmpres){
//插入map中的vector<int>部分
res.push_back(i.second);
}
return res;
}
};
矩阵上的bfs
(题目8)
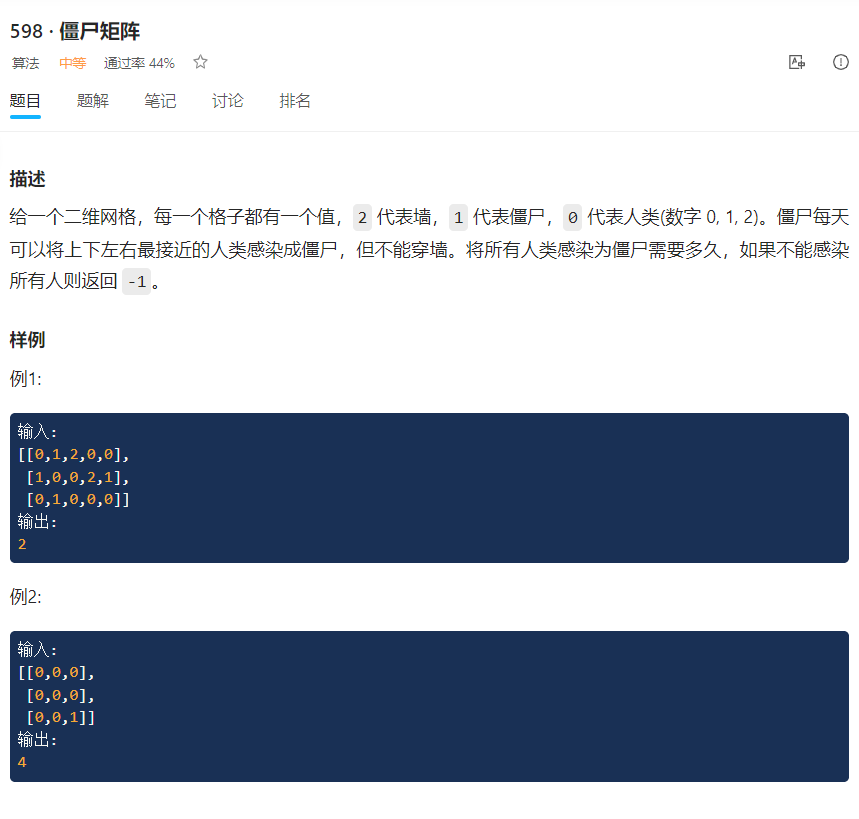
class point{
public:
int x,y;
point(int _x,int _y)
:x(_x),y(_y)
{
}
};
class Solution {
public:
int zombie(vector<vector<int>> &grid) {
int cnt=0,n=grid.size();
if(n==0){
return 0;
}
int m=grid[0].size();
if(m==0){
return 0;
}
queue<point>q;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(grid[i][j]==1){
q.push(point(i,j));
}
}
}
int day[4][2]={
{
1,0},{
-1,0},{
0,-1},{
0,1}};
while(!q.empty()){
int size=q.size();
cnt++;
//感染上下左右的点
for(int i=0;i<size;i++){
point head=q.front();q.pop();
for(int k=0;k<4;k++){
int x=head.x+day[k][0];
int y=head.y+day[k][1];
if(x>=0&&x<n&&y>=0&&y<m&&grid[x][y]==0){
grid[x][y]=1;
q.push(point(x,y));
}
}
}
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
//如果还有0表示还有幸存者
if(grid[i][j]==0){
return -1;
}
}
}
//需要减一,在刚进入队列时多加了一次
return cnt-1;
}
};
(题目9)
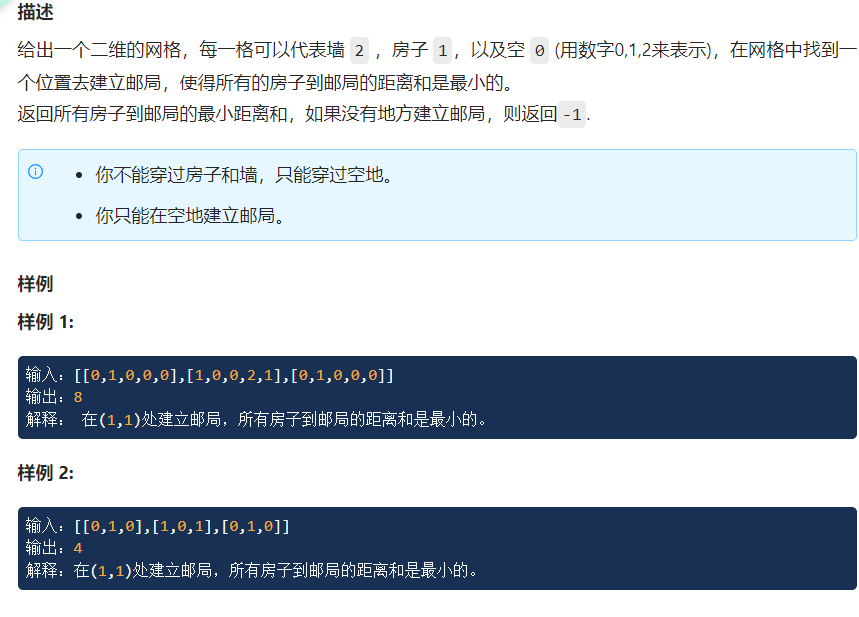
这个题的解题思路和地图分析相似。
(地图分析)[573 · 邮局的建立 II - LintCode]
/* 直接思路: 1.遍历所有的空地点 2.对每个空地点用bfs到所有house的距离 3.用打擂台的方式求最短距离 */
class Solution {
public:
#define WALL 2
#define HOUSE 1
#define EMPT 0
const vector<vector<int>> direct= {
{
1,0}, {
0,1}, {
-1,0}, {
0,-1}};
int minDis;
int numHouse;
class Coord {
public:
int x, y;
Coord(int x, int y) : x(x), y(y) {
};
};
int shortestDistance(vector<vector<int>> &grid) {
// write your code here
if (grid.size() == 0) {
return -1;
}
minDis = -1;
numOfHouse(grid);
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
if (grid[i][j] == EMPT) {
Coord pos(i, j);
findDis(pos, grid);
}
}
}
return minDis;
}
void numOfHouse(vector<vector<int>> &grid) {
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
if (grid[i][j] == HOUSE) {
numHouse++;
}
}
}
}
bool isInBound(vector<vector<int>> &grid, int x, int y) {
if (x < 0 || x >= grid.size() || y < 0 || y >= grid[0].size()) {
return 0;
} else {
return 1;
}
}
void findDis(Coord &pos, vector<vector<int>> &grid) {
vector<vector<bool>> visited(grid.size(), vector<bool>(grid[0].size()));
queue<Coord> q;
q.push(pos);
visited[pos.x][pos.y] = 1;
int dis = 0;
int visitedHouse = 0;
int step = 0;
while (!q.empty()) {
int qsize = q.size();
step++;
for (int i = 0; i < qsize; i++) {
Coord cd = q.front();
q.pop();
for (int j = 0; j < direct.size(); j++) {
int x = cd.x + direct[j][0];
int y = cd.y + direct[j][1];
if (isInBound(grid, x, y) && visited[x][y] == 0) {
if (grid[x][y] == HOUSE) {
dis += step;
if (minDis != -1 && dis >= minDis) {
return;
}
visitedHouse++;
if (visitedHouse == numHouse) {
minDis = dis;
return;
}
}
if (grid[x][y] == EMPT) {
q.push(Coord(x, y));
}
visited[x][y] = 1;
}
}
}
}
}
};
class point{
public:
int x,y;
point(int _x,int _y)
:x(_x),y(_y)
{
}
};
class Solution {
public:
int dir[4][2]={
{
1,0},{
-1,0},{
0,1},{
0,-1}};
//记录房子的数量
int mindis=INT_MAX,numhouse=0;
int shortestDistance(vector<vector<int>> &grid) {
int n=grid.size(),m=grid[0].size();
if(n==0||m==0){
return -1;
}
numofhouse(grid);
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
//如果是一块空地,就找他的所有距离
if(grid[i][j]==0){
point pos(i,j);
finddis(pos,grid);
}
}
}
return mindis;
}
void numofhouse(vector<vector<int>>&grid){
for(int i=0;i<grid.size();i++){
for(int j=0;j<grid[0].size();j++){
if(grid[i][j]==1){
numhouse++;
}
}
}
}
bool isinfound(int x,int y,vector<vector<int>>&grid){
if(x<0||x>=grid.size()||y<0||y>=grid[0].size()){
return false;
}
return true;
}
void finddis(point&p,vector<vector<int>>&grid){
//记录该点是否被遍历
vector<vector<bool>>visit(grid.size(),vector<bool>(grid[0].size()));
queue<point>q;
q.push(p);
//visit记录访问房子的数量,distance记录距离
visit[p.x][p.y]=1;
int visithouse=0,step=0,distance=0;
while(!q.empty()){
step++;
int size=q.size();
for(int i=0;i<size;i++){
point head=q.front();q.pop();
for(int k=0;k<4;k++){
int x=head.x+dir[k][0];
int y=head.y+dir[k][1];
if(isinfound(x,y,grid)&&visit[x][y]==0)
{
if(grid[x][y]==1){
distance+=step;
visithouse++;
if(visithouse==numhouse){
mindis=min(distance,mindis);
return ;
}
}
//如果是没有被访问的空点,就加入队列中
if(grid[x][y]==0){
q.push(point(x,y));
}
visit[x][y]==1;
}
}
}
}
}
};
边栏推荐
- De debugging (set the main thread as hidden debugging to destroy the debugging Channel & debugger detection)
- Clickhouse synchronization MySQL (based on materialization engine)
- About authentication services (front and back, login, registration and exit, permission management)
- 线程基础知识
- [positioning in JS]
- Kuboard
- MySQL winter vacation self-study 2022 11 (9)
- 面试汇总:这是一份全面&详细的Android面试指南
- Operation flow of UE4 DMX and grandma2 onpc 3.1.2.5
- How to make the listbox scroll automatically when adding a new item- How can I have a ListBox auto-scroll when a new item is added?
猜你喜欢
【无标题】
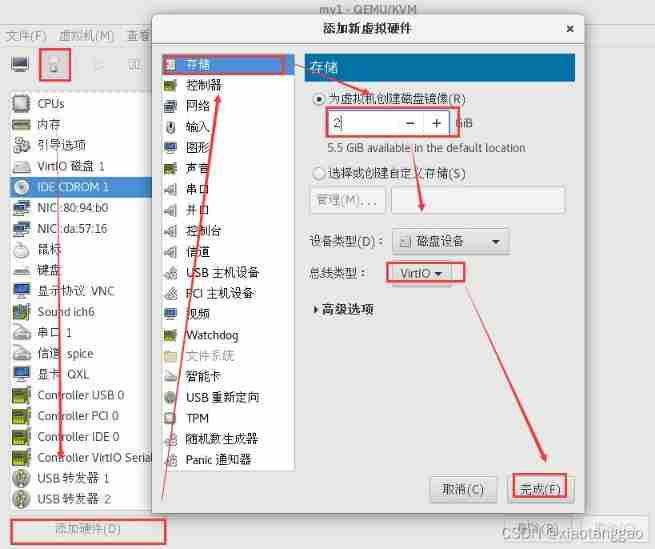
KVM virtualization

Easy processing of ten-year futures and stock market data -- Application of tdengine in Tongxinyuan fund
![[vérification sur le Web - divulgation du code source] obtenir la méthode du code source et utiliser des outils](/img/ea/84e67a1fca0e12cc4452c744c242b4.png)
[vérification sur le Web - divulgation du code source] obtenir la méthode du code source et utiliser des outils
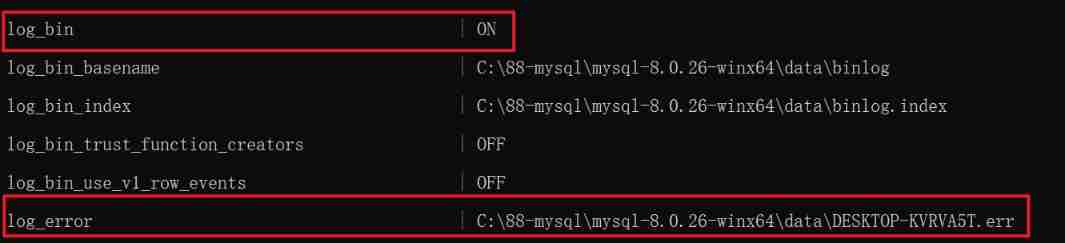
About MySQL database connection exceptions
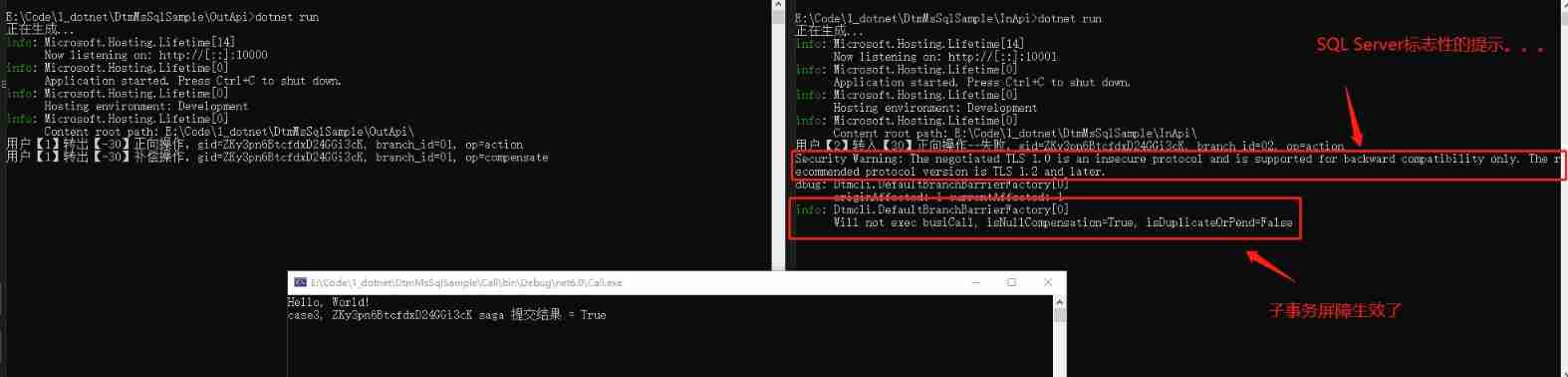
Talk about the SQL server version of DTM sub transaction barrier function
![[wp]bmzclub writeup of several questions](/img/15/2838b93a605b09d3e2996f6067775c.png)
[wp]bmzclub writeup of several questions
![[groovy] groovy environment setup (download groovy | install groovy | configure groovy environment variables)](/img/99/bb05b6c48a9e70ca7ff77733d954b9.jpg)
[groovy] groovy environment setup (download groovy | install groovy | configure groovy environment variables)
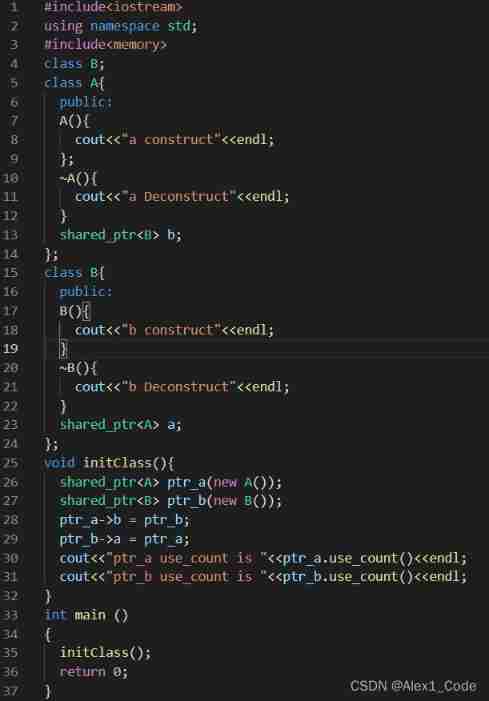
Smart pointer shared_ PTR and weak_ Difference of PTR
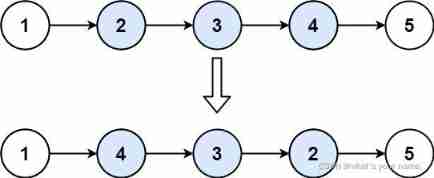
Leetcode92. reverse linked list II
随机推荐
De debugging (set the main thread as hidden debugging to destroy the debugging Channel & debugger detection)
官宣!第三届云原生编程挑战赛正式启动!
040. (2.9) relieved
Delphi free memory
我就一写代码的,王总整天和我谈格局...
MySQL winter vacation self-study 2022 11 (10)
問下,這個ADB mysql支持sqlserver嗎?
[an Xun cup 2019] not file upload
【web源码-代码审计方法】审计技巧及审计工具
UI自动化测试从此告别手动下载浏览器驱动
Why is there a reincarnation of 60 years instead of 120 years in the tiangan dizhi chronology
[groovy] groovy environment setup (download groovy | install groovy | configure groovy environment variables)
Redis之Jedis如何使用
反絮凝剂-氨碘肽滴眼液
The latest blind box mall, which has been repaired very popular these days, has complete open source operation source code
Google Chrome CSS will not update unless the cache is cleared - Google Chrome CSS doesn't update unless clear cache
postman和postman interceptor的安装
Clickhouse物化视图
An elegant program for Euclid‘s algorithm
speed or tempo in classical music